ゼロから作る Deep Learning (2) 自然言語処理編をJulia 1.0.2でやってみる

この記事は Julia Advent Calendar 2018 の14日目の記事です。

---

TL; DR

• ゼロから作るDeep Learning② 自然言語処理編の一部を，Julia 1.0.2の習得を含めてやってみます．

ゼロから作るDeep Learning ❷ ―自然言語処理編

posted with amazlet at 18.12.10

斎藤 康毅
オライリージャパン
売り上げランキング: 1,084

Amazon.co.jpで詳細を見る

準備

• @antimon2 さんが「ゼロから作るDeep Learning」で作成していたDLScratch.jlを見て雰囲気を掴む
  • ただしJuliaのバージョンが当時のもの (0.5.x) なので，1.0.2では動かない部分もある
• これをForkしてきて1.0.2で動く雰囲気のコードを作成: https://github.com/cocomoff/DLScratch.jl
• よくハマったポイント
  • broadcastに関して呼び出し方の変更(expとexp.)
  • パッケージの整理(例. using LinearAlgebraが必要)
  • 型の定義方法(immutable -> struct, mutable structなど)が変更
  • ジェネリクスの型パラメータ{T}の受け渡し方法
    • 今まで: function{T}()
    • 最近の: function() where {T}
• 他にもいくつかなくなった関数がある（名前変更含む）ので，その都度調べて再実装

1章

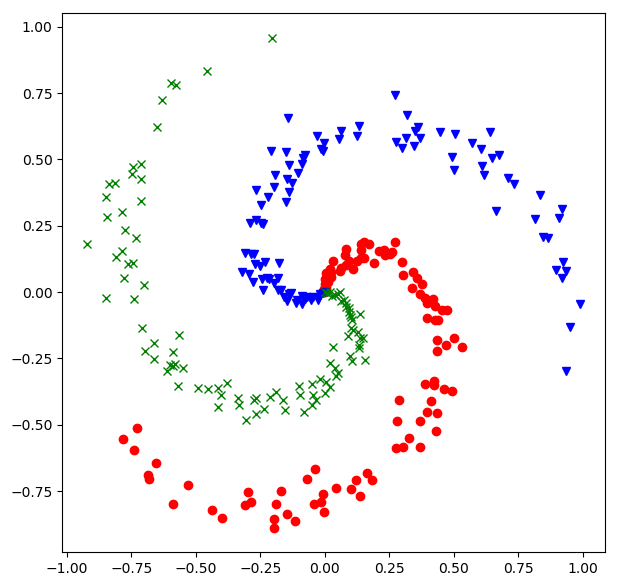
• Pythonで作成したspiral dataをJuliaで読めるようにする
  • https://github.com/cocomoff/DLScratch2.jl/blob/master/data/sprial.dat
• Julia 1.0.2 + PyPlotでの可視化

using PyPlot
using DelimitedFiles
X = readdlm("data/sprial.dat")
X1 = X[1:100, :];
X2 = X[101:200, :];
X3 = X[201:end, :];
plot(X1[:, 1], X1[:, 2], "ro")
plot(X2[:, 1], X2[:, 2], "bv")
plot(X3[:, 1], X3[:, 2], "gx")

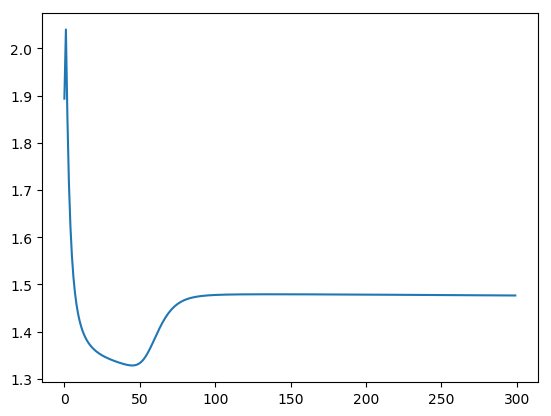
• SpiralとTwoLayerNet
  • notebook: https://github.com/cocomoff/DLScratch2.jl/blob/master/chapter1_spiral.ipynb
• ロスが収束していないのでどこか悪い感じがする

自然言語処理っぽい操作を行う

2章

• 行列操作はPython/Numpyと同じ形式でほとんど可能（using LinearAlgebra）が必要
• 前処理

using LinearAlgebra
text = "You say goodbye and I say hello."
text = lowercase(text)
text = replace(text, "." => " .")
words = split(text, " ")
word_to_id = Dict{String, Int}()
id_to_word = Dict{Int, String}()
for word in words
    word = String(word)
    if !haskey(word_to_id, word)
        new_id = length(word_to_id)
        word_to_id[word] = new_id
        id_to_word[new_id] = word
    end
end
@show word_to_id;  # word_to_id = Dict("say"=>1,"goodbye"=>2,"you"=>0,"hello"=>5,"."=>6,"and"=>3,"i"=>4)
@show id_to_word;  # id_to_word = Dict(0=>"you",4=>"i",2=>"goodbye",3=>"and",5=>"hello",6=>".",1=>"say")

• 共起行列と類似度の計算

function create_co_matrix(corpus, vocab_size; window_size=1)
    corpus_size = length(corpus)
    co_matrix = zeros(Int64, vocab_size, vocab_size)
    
    for (idx, word_id) in enumerate(corpus)
        for i in 1:window_size
            left_idx = idx - i
            right_idx = idx + i
            
            if left_idx >= 1
                left_word_id = corpus[left_idx]
                co_matrix[word_id, left_word_id] += 1
            end
                
            if right_idx <= corpus_size
                right_word_id = corpus[right_idx]
                co_matrix[word_id, right_word_id] += 1
            end
        end
    end
    
    return co_matrix
end

function cos_similarity(x, y; ϵ=1e-8)
    nx = x ./ sqrt(sum(x .^ 2) + ϵ)
    ny = y ./ sqrt(sum(y .^ 2) + ϵ)
    return dot(nx, ny)
end

# example
C = create_co_matrix(corpus, 7)
c0 = C[word_to_id["you"], :];
c1 = C[word_to_id["i"], :];
println(cos_similarity(c0, c1))
# 0.7071067758832467

• PPMIやSVD
  • PPMIでは普通にfor文をかいているけど，Pythonより安心できる（個人差あり）

function PPMI(C; verbose=false, ϵ=1e-8)
    M = zeros(Float64, size(C))
    N = sum(C)
    S = sum(C, dims=1)
    total = size(C)[1] * size(C)[2]
    count = 0
    
    for i in 1:size(C)[1]
        for j in 1:size(C)[2]
            pmi = log2(C[i, j] * N / (S[j] * S[i]) + ϵ)
            M[i, j] = max(0, pmi)
            
            if verbose
                count += 1
                if count % (total // 100) == 0
                    println("$(100 * cnt / total) done")
                end
            end
        end
    end
    
    return M
end

# SVDもそのまま
W = PPMI(C)
U, S, V = svd(W)

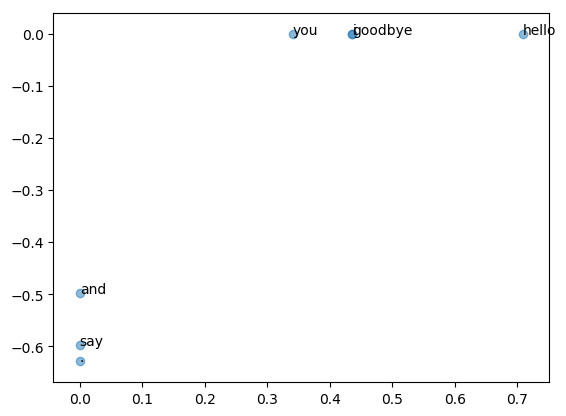
# PyPlotで描画 (ほとんどPythonと同じ)
figure()
for (word, wid) in word_to_id
    annotate(word, (U[wid, 1], U[wid, 2]))
end
scatter(U[:, 1], U[:, 2], alpha=0.5)

5章

• RNNの実装をやってみる．PythonとDLScratch.jlを参考にすると次のようになる．

  • 1つのRNNユニットなので，例えばPyTorchで言うところのRNNCellに相当する

• Notebookで丁寧にデバッグしてみる

  • Python版(書籍のgithubより抜粋): https://github.com/cocomoff/DLScratch2.jl/blob/master/py_chapter5.ipynb
  • Julia版: https://github.com/cocomoff/DLScratch2.jl/blob/master/chapter5.ipynb

例えば$h_{t}$を計算する式とjuliaとpythonを比較してみる

• 式

$$h_{t} = \tanh(h_{t-1}W_h + x_t W_x + b)$$

• Python

t = np.dot(h_prev, Wh) + np.dot(x, Wx) + b
h_next = np.tanh(t)

• Julia

t = h_prev * rnn.Wh + x * rnn.Wx .+ b  
h_next = tanh.(t)

RNNCell全体の実装

mutable struct RNN{T}
    Wx::AbstractMatrix{T}
    Wh::AbstractMatrix{T}
    b::AbstractMatrix{T}
    dWx::AbstractMatrix{T}
    dWh::AbstractMatrix{T}
    db::AbstractMatrix{T}
    
    # self.cache @ python
    x::AbstractMatrix{T}
    hp::AbstractMatrix{T}
    hn::AbstractMatrix{T}

    function (::Type{RNN})(Wx::AbstractMatrix{T}, Wh::AbstractMatrix{T}, b::AbstractMatrix{T}) where {T}
        layer = new{T}()
        layer.Wx = Wx
        layer.Wh = Wh
        layer.b = b
        layer.dWx = zeros(size(Wx))
        layer.dWh = zeros(size(Wh))
        layer.db = zeros(size(b))
        layer
    end
end

function forward(rnn::RNN{T}, x::AbstractMatrix{T}, h_prev::AbstractMatrix{T}) where {T}
    # Eq.(5.9)
    t = h_prev * rnn.Wh + x * rnn.Wx .+ b  
    h_next = tanh.(t)
    
    rnn.x = x
    rnn.hn = h_next
    rnn.hp = h_prev
    return h_next
end

function backward(rnn::RNN{T}, dh_next::AbstractMatrix{T}) where{T}
    x, h_prev, h_next = rnn.x, rnn.hp, rnn.hn
    dt = dh_next .* (1 .- h_next .^ 2)
    dh_prev = dt * Wh'
    rnn.dWh = h_prev' * dt
    rnn.dWx = x' * dt
    rnn.db .= sum(dt, dims=1)
    dx = dt * Wx'
    return dx, dh_prev
end

まとめ

• 行列の形に気をつけながら書いていくと，いい感じに書いていける
  • 個人的にはブロードキャストと行列の型がイマイチ脳みそにハマってないのか，しょっちゅうバグを起こしてしまった
• DLScratch.jlが最高に参考になる（感謝）
• 現状DLScratch2.jlを書いてみているけど，ソースコード/Notebookをちゃんと整理したらまともに更新します…（休みがいろいろ重なって間に合わなかった．12月中に期待）
  • https://github.com/cocomoff/DLScratch2.jl