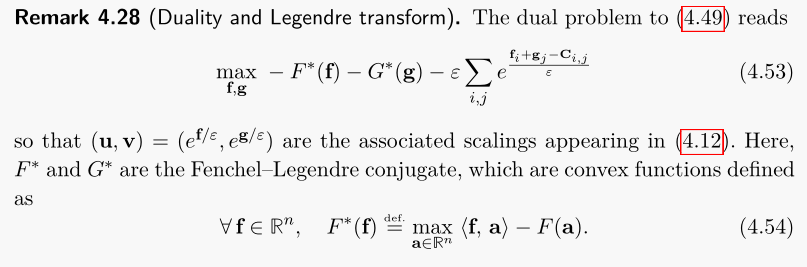More than 5 years have passed since last update.

Computational Optimal Transport 精読会記録 (#18: 4.6)

Last updated at 2019-08-07Posted at 2019-08-07

背景

エントロピー正則化付き最適化問題
- Primal (4.2) $L^\varepsilon_C({\bf a}, {\bf b}) = \min_{{\bf P}\in U({\bf a},{\bf b})} \langle {\bf P}, C\rangle - \varepsilon H({\bf P})$
- Dual (4.30) $L_C^\varepsilon(a,b) = \max_{f, g} \langle f, a\rangle + \langle g, b\rangle - \varepsilon \langle \exp(f/\varepsilon), K\exp(g/\varepsilon)\rangle$
Sinkhornアルゴリズム最高 → ちゃんと収束するし，高速化できるよ．安定化するためにはLogドメインが必須だよ．
- $\mathbf{u}^{(l+1)} = \frac{\mathbf{a}}{\mathbf{Kv}^{(l)}}$, $\mathbf{v}^{(l+1)} = \frac{\mathbf{b}}{\mathbf{K}^T\mathbf{u}^{(l + 1)}}$
エントロピー正則化で解いた解は，元の解に対してバウンドになっていて使える（収束していれば）
今回: 一般化Sinkhorn

Sinkhornを導入した§4.2において，SinkhornアルゴリズムがKL-div.のProjと関連があったりするという話を書いた
似たような路線で，一般化されたSinkhornについて議論する．具体的には$P1_m = a, P^T 1_n = b$という今までの制約が関数$F, G$で一般化された問題(4.49)を議論する．これは今までとは違って$F$と$G$が入ることで制約なし最適化になっている．例えば$F$と$G$を支持関数にすれば同じ．

$$\text{(4.49): } \min_{P} \langle C, P\rangle - \varepsilon H(P) + F(P1_m) + G(P^T 1_n)$$

面白いことに，(4.49)の最適化問題は，Sinkhornと同じ解の形をもつ．これは$P1_m=f, P^T1_n=g$などの変数を仮に置いてラグランジアンを考えると，$P$について偏微分をする仮定で消され，Sinkhornの解の形を議論したProp 4.3(おそらく)と同じ式変形が可能なため．
様々な最近の論文(Peyre 2015, Frogner et al. 2015, Chizat et al. 2019, Karlsson and Ringh 2016)のお陰で，この式は次のような解放で定式化される
- $u \leftarrow \frac{1}{Kv} \mathrm{Prox}_F^\mathbf{KL}(Kv)$
- $v \leftarrow \frac{1}{K^Tu} \mathrm{Prox}_G^\mathbf{KL}(K^Tu)$
- もともとのSinkhornが$a, b$を割るだけだった部分が，Proxになった
Proxの定義
- $\mathrm{Prox}_F^\mathbf{KL}(u) = \arg\min_{u'} KL(u'\mid u) + F(u')$
- 式からも，$F$が仮に指示関数の場合，$u'=a$の解しか存在しないため，これはSinkhornと一致すると分かる
特に証明などは出てこない（論文レベル）
argminとProxの性質から，例えば$F(u)=\sum_i F_i(u_i)$のようにelement-wiseになっているとき，Proxもelement-wiseで良い