背景
- 前回: Computational Optimal Transport 精読会 記録 (#3: 2.5前半)は3/25に開催,今回は4/3に開催
- 職場でCOTを読んでおり,{自己満足,復習,将来のため}などの理由で記録をしている
今回の範囲の内容
- Kantorovich問題の双対問題について(後半)と残りの諸定理について(測度論パートは含まない)
アンチョコ
-
Kantorovich problem: $L_C(\mathbf{a,b}) = \min_{\mathrm{P}\in U(\mathbf{a, b})} \langle C, P \rangle$
- coupling matrix: $U(a, b) = \{\mathrm{P}\in \mathbb{R}_+^{n\times m}\mid \mathrm{P} \mathbb{1}_m = \mathbf{a}, \mathbf{P}^T \mathbb{1}_n = \mathbf{b} \}$
-
Dual problem $L_C(\mathbf{a,b}) = \max_{(\mathbf{f, g})\in R(C)} \langle \mathbf{f, a}\rangle + \langle \mathbf{g, b}\rangle$
- ただし $R(C) = \{(\mathbf{f,g})\in\mathbb{R}^n\times \mathbb{R}^m \mid \mathbf{f \oplus g} \leq C\}$
Dual Problemの解釈
- $a$を原材料置き場(倉庫),$b$を工場と考え,$a$から$b$へ輸送する問題を考える
- 主問題を解ける場合,その最適化解 $P^\star$ のように材料を輸送すればよい
- 主問題を解くリソースが存在しないと仮定し,集配側(a側)と分配側(b側)で仕事をアウトソーシングすると想定する
- アウトソーシングする場合の価格を$\bf f$と$\bf g$で考える
- 考え方: 輸送する側は価格を最小化したい,アウトソーシングされる側は得られる報酬を最大化したい
- アウトソーシングを請け負う側が得られる報酬とは要するに $\langle \bf f, a\rangle + \langle \bf g, b\rangle$ である
- 補足: 両方同時に上げたい($\bf f$で減った分は$\bf g$側に入れることで解消できるイメージ)
- 輸送する側は設定された価格$\bf f, g$が正しいか(reasonable)を確認しないといけない
- 主問題を解けば分かるが,主問題を解くリソースがない
- けれども$\bf f_i, g_j$が分かっていれば,これと$C_{i,j}$を比較すれば良い
- $f_i + g_j \leq C_{i,j}$であれば,アウトソーシングをOKする
- この条件が満たされていれば,双対問題は主問題で計算されるコストと比較して良いかどうか確認できる
2.6 Special Cases
- 本来主問題$L_C(a,b)$を解くために何らかの計算リソースが必要となるが,いくつかの特別な場合においてこれは簡単に計算できる
Remark 2.26
-
$\bf C = \mathbb{1}_{n\times n} - \mathbb{I}_n$ であるような場合の1-Wasserstein distance
- 注: 対角線が0,他が1であるようなコスト行列
- $L_C(a,b) = \frac{1}{2} ||a - b||_1$ (注: ここでノルムに1/2が必要だけどarXiv版では抜けている)
-
証明の考え方
- 対角線のコストが0なので,最適解について対角線に可能な限り輸送するのが良い
- 輸送できる最大量はmarginalの制約から各$i$について$\min(a_i,b_i)$であり,仮に$a_i<b_i$であれば,$a$の方向(行方向)はすべて$0$になる,逆に$0$にならない側の輸送量は$|a_i - b_i|$となっている(対角線で送る分の残り)
- これを全部の輸送パターンでやっていくと,全体で送る量は$\sum_{i} |a_i - b_i|$の半分になって,これは主張になる
Remark 2.27
- 1-Dのヒストグラムを考えソートされているような問題を考え,それぞれ$1/n$ずつ重みが置かれている状況を想定する
- このとき$\mathcal{W}_p(\alpha, \beta)^p = \frac{1}{n} \sum_{i} |x_i - y_i|^p$ となる
- 意味: ソートされた順でマッチングしていくような計算で良い
- 証明の考え方
- 一番簡単なケースを考える: それぞれ2点ずつで$x_1, y_1, x_2, y_2$,各点に$\frac{1}{2}$の山が置かれているような離散測度
- これを考えるには以下の3ケースにおいて,$x_1\mapsto y_1, x_2\mapsto y_2$が最良になることを示す
- $x_1 < y_1 < x_2 < y_2$のケース
- $|x_1 - y_1| = \alpha, |y_1-x_2| = \beta, |x_2 - y_2| = \gamma$
- $x_1 \mapsto y_2, x_2\mapsto y_1$と比較して明らか
- $x_1 < y_1 < y_2 < x_2$のケース
- $|x_1 - y_1| = \alpha, |y_1-y_2| = \beta, |y_2 - x_2| = \gamma$
- 上と同じ
- $x_1 < x_2 < y_1 < y_2$のケース
- $|x_1 - x_1| = \alpha, |x_2-y_1| = \beta, |y_1 - y_2| = \gamma$
- 入れ替えた場合もコストを計算して$p$ノルムの場合証明が必要
- 適当な証明を思いつくといけるらしい
- $x_1 < y_1 < x_2 < y_2$のケース
Remark 2.29
- Histogram equalizationの説明だが,必ずしも図2.10とリンクしているわけではないので注意
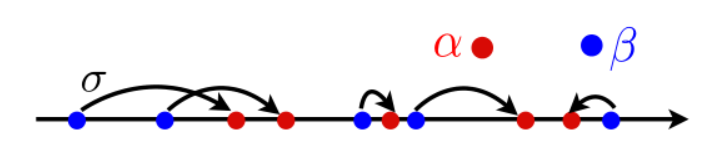
- 絵のベクトルをソートする関数$\sigma$を頑張って読み解く
次回
次回からは§3をやっていく