データサイエンス入門シリーズが刊行されはじめたので,気分転換に最適化手法入門を読みました.帯に「Pythonですぐに実践」と書いてあったので,どんなものかな?と思って公式のサンプルコードと本を確認すると
- §3 非線形計画
- §4 凸計画
- §6 近似解法と発見的解放
- §7 整数計画
の章はあまりPythonコードがなくて素人(私)は詰みそうだったので,Pythonでコードを書きました.この記事は§3の一部です.
例(式3.3)
次のような2変数関数に対して,勾配とヘッセ行列を用いた最適化法を議論します.ここでは勾配を利用する一次の方法について実装してみます.
$$f(\mathbf{x}) = (x_1 - 3)^2 + x_1 x_2 + \frac{1}{16}x_2^4 + (x_2 - 1)^2$$
関数形が簡単なので,$x_1$と$x_2$についての偏導関数は閉じた式で書けます.$x_1$について偏微分すると
$$\frac{\partial f}{\partial x_1} = 2(x_1 - 3) + x_2$$
となり,$x_2$について偏微分すると
$$\frac{\partial f}{\partial x_2} = x_1 + \frac{1}{4}x_2^3 + 2(x_2 - 1)$$
となります.すべてPythonの関数で書いておきましょう.ついでにそれぞれの偏微分をベクトル(np.array)で計算する関数も書いておきます.numpyを真面目に使う場合には,x1, x2と分けるのではなく,2次元のnp.arrayを使った方が良かったかもしれません.
def f(x1, x2):
return (x1 - 3) ** 2 + x1 * x2 + 1.0 / 16.0 * x2 ** 4 + (x2 - 1) ** 2
def fx1(x1, x2):
return 2 * (x1 - 3) + x2
def fx2(x1, x2):
return x1 + 1.0 / 4.0 * x2 ** 3 + 2 * (x2 - 1)
def fx1x2(x1, x2):
return np.array([fx1(x1, x2), fx2(x1, x2)])
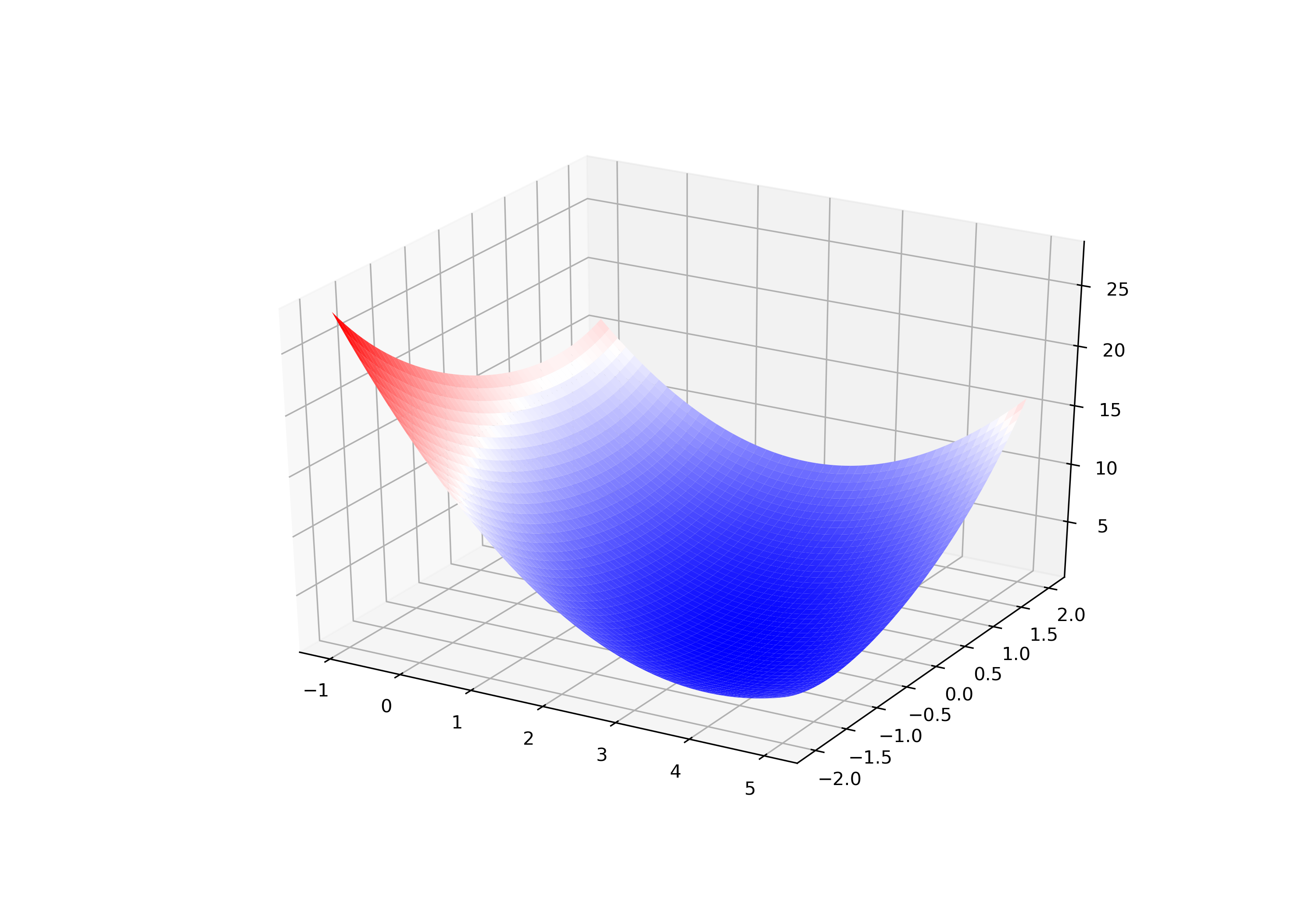
3次元プロットと等高線プロット(図3.2)
matplotlibのAxes3Dを利用して3次元プロットを描画します.ついでに等高線を描くためにcontourを使って描画します.Axes3Dの真面目な解説はQiitaなどにもいろいろあるので参考にしてください.軸の範囲は適当に本書に合わせる雰囲気にしておきます.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
N = 1000
x1 = np.linspace(-1, 5, N)
x2 = np.linspace(-2, 2, N)
X1, X2 = np.meshgrid(x1, x2)
Z = f(X1, X2)
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_surface(X1, X2, Z, cmap='bwr', linewidth=0)
plt.savefig("graph1.png", dpi=300)
plt.show()
plt.close()
このような感じになります.ちょっと回転角度が本と合ってないですが(適当なので),それっぽい図になりました.
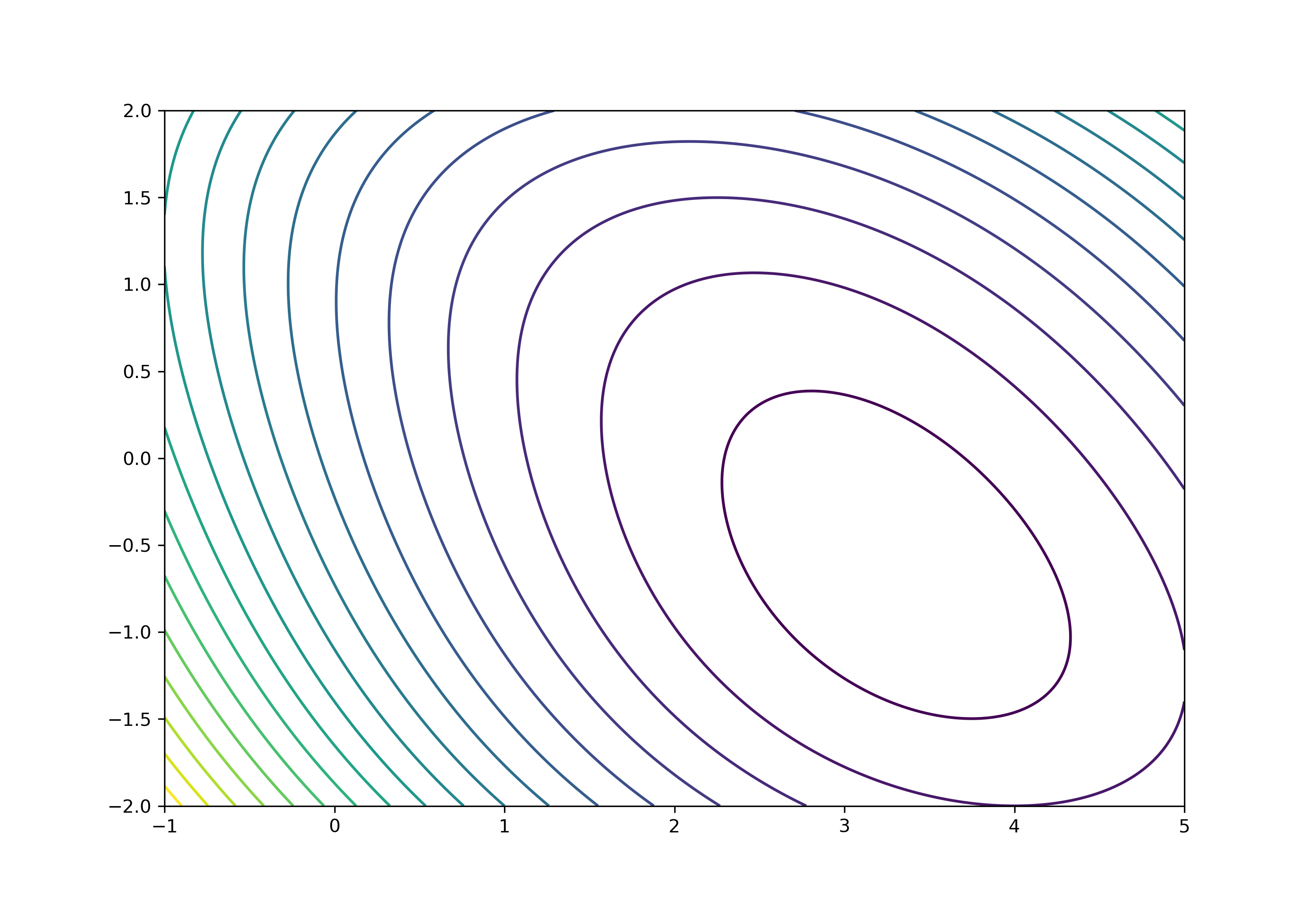
等高線を描く場合は,projection='3d'の指定をなくして,contourを利用します.
fig = plt.figure(figsize=(10, 7))
# ax = fig.add_subplot(111, projection='3d')
ax = fig.add_subplot(111)
ax.contour(X1, X2, Z, 25)
plt.savefig("graph2.png", dpi=300)
plt.tight_layout()
plt.show()
このようになります.良い感じです.
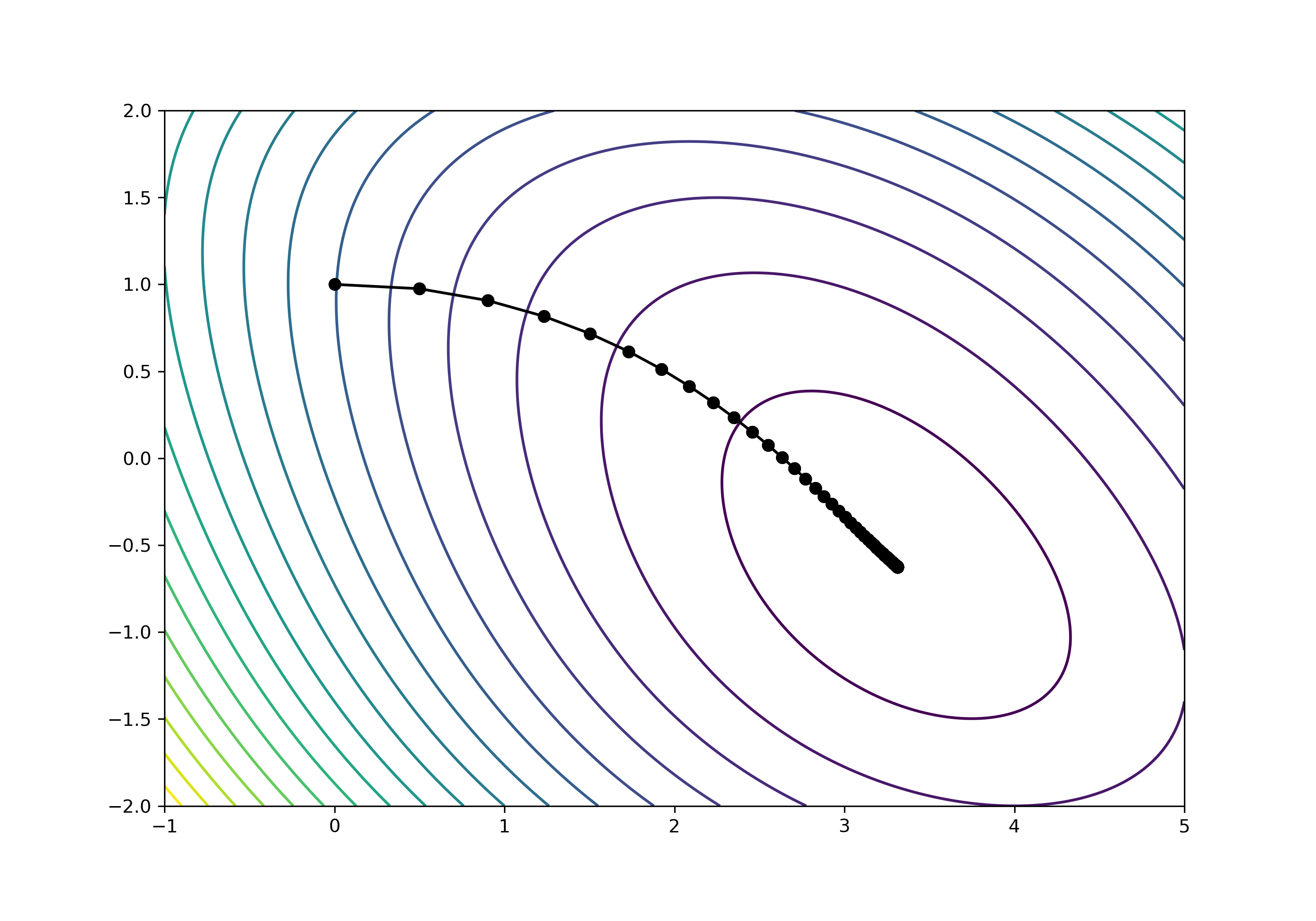
最急降下法
勾配ベクトルを$\nabla f(\mathbf{x})$ の方向に降りていけば良いという手法ですね(詳細はテキスト).勾配は閉じた価値で実装してあるので,適当なパラメータ $\alpha=0.1$ として,初期値 $\mathbf{x}_0=\begin{pmatrix}0 & 1\end{pmatrix}$ として1000回程度反復させてみます(といいつつ,変化量が小さくなったらbreakします).ついでに各$\mathbf{x}_n$を保存しておいて描画します.
x0 = np.array([0, 1])
d0 = np.array([0, 1])
list_of_x = []
n_iter = 1000
α = 0.1
for n in range(n_iter):
# 再急降下法
dn = -fx1x2(*x0)
list_of_x.append(x0)
x_new = x0 + α * dn
if np.linalg.norm(x_new - x0) < 1e-6:
break
x0 = x_new
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111)
ax.contour(X1, X2, Z, 25)
for i in range(len(list_of_x) - 1):
xi, xj = list_of_x[i:i+2]
ax.plot([xi[0], xj[0]], [xi[1], xj[1]], marker='o', color='k')
plt.savefig("graph3.png", dpi=300)
plt.tight_layout()
plt.show()
plt.close()
次のようになります.良い感じですね!
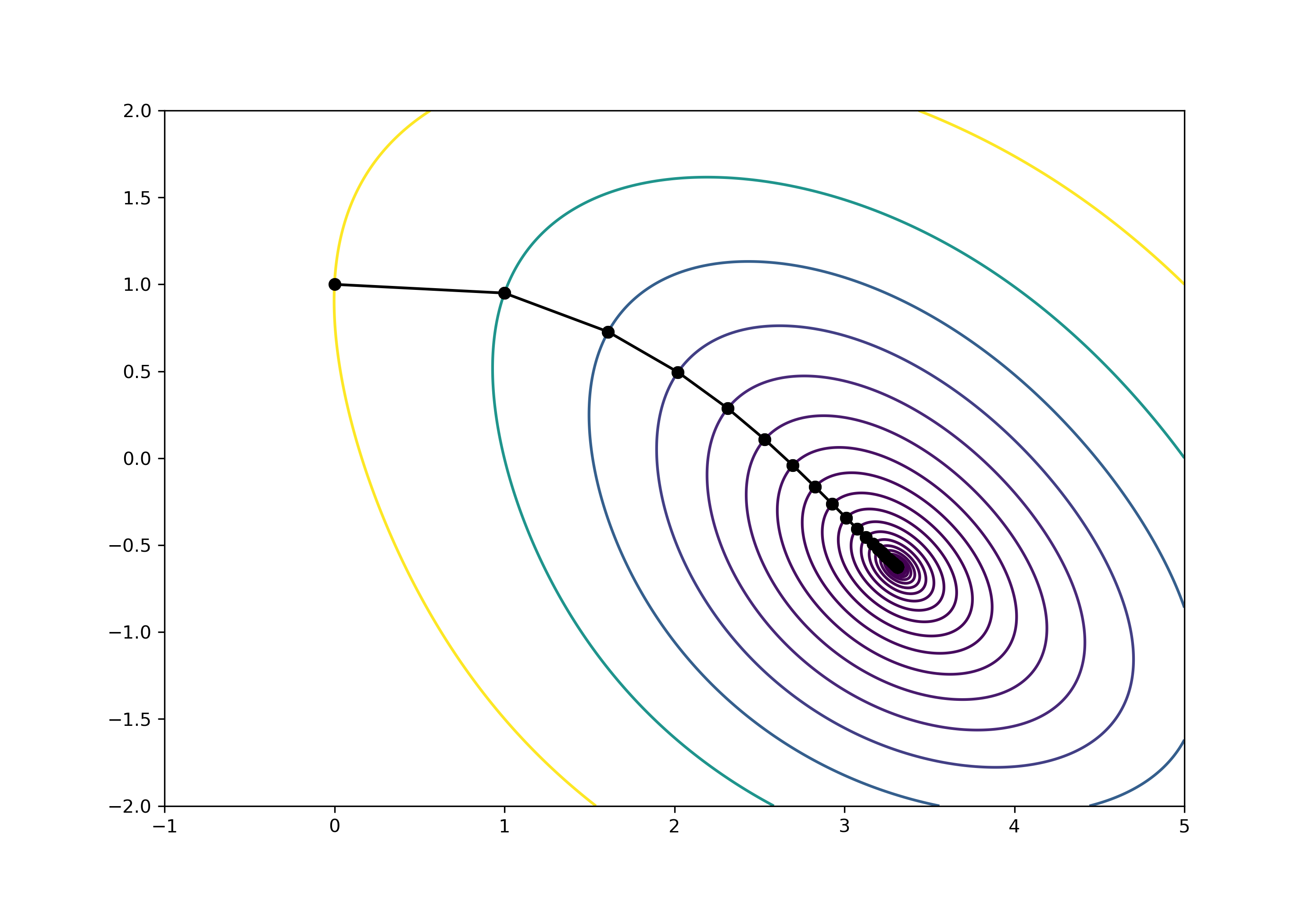
ところで最急降下法の勾配方向が投稿線に直交するという話を聞いたことあるかもしれません.これを確かめるために,各地点の $\mathbf{x}_n$ に合わせて等高線を引いてみることにしましょう.今,list_of_xという配列に各地店の値が入っているので,これをソートします(ソートしないと怒られる).ソートした値を投稿線の線を引く値に指定するために,levelsとして与えます.
ylevels = [f(x1, x2) for (x1, x2) in list_of_x]
ylevels = sorted(ylevels, reverse=False)
ax.contour(X1, X2, Z, levels=ylevels)
次のような図になります.良い感じでした.
直線探索法や§4の近接勾配法,交互方向乗数法についてもプログラムを書こうと思って途中まで書いたのですが,記事を書くのが疲れたのでそのうち公開します.