はじめに(なぜこれを選んだか)
サンプリングは積分計算が難しい状況で採用される手法の一つですが、自分は昔からサンプリング系の手法がイマイチ理解できていません(例えばPRML§11とかよく分からない ┐(´ー`)┌ )。しかし、最近たまにサンプリング系の手法を使っている論文を読むことがあるので、基本的なところから勉強しておくことにしました。
最近社畜業務で電車で揺られながら
という本を読んでいたので、4章・5章で出てくるM-HサンプリングとHMC法をまとめたいと思います。中身はほぼ本の例題通りです。本当は付録BあたりまでやってスライスサンプリングとNUTSまで行きたかったですが、仕事が爆発して時間が足りませんでした(後で追加でやっておくつもりです)。
あと以下のコードは整理したらgithubかbitbucketにでも上げておきます。
例題
稀に起こる事象の確率分布としてポアソン分布と、その事前分布としてガンマ分布を利用します。ガンマ分布がポアソン分布の共役事前分布なのでサンプリングはそもそも不要ですが、例題として使います(本中§3通り)。
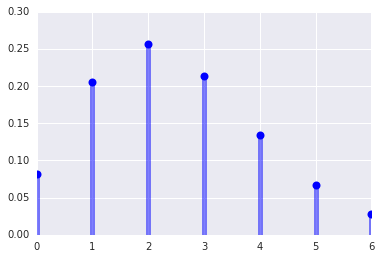
ポアソン分布の図示
import numpy as np
import scipy.stats as sst
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
### ポアソン分布(平均2.5)の例
from scipy.stats import poisson
mu = 2.5
x = np.arange(poisson.ppf(0.01, mu), poisson.ppf(0.99, mu))
plt.plot(x, poisson.pmf(x, mu), 'bo', ms=8, label='poisson pml')
plt.vlines(x, 0, poisson.pmf(x, mu), colors='b', lw=5, alpha=0.5)
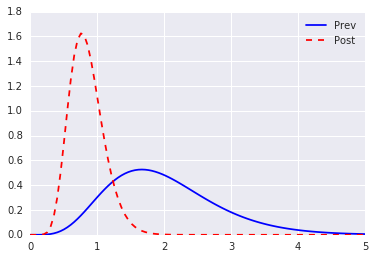
事前分布としてのガンマ分布導入と事後分布の計算
適当にポアソン分布らしきデータ(0, 1, 0, 0, 2, 0, 1, 0, 0, 1)を観測したとして、事後分布を計算する。上に書いたとおり、そもそも共役事前分布なので、なまけて事後分布の形が分かる。
# データ
x_data = np.array([0, 1, 0, 0, 2, 0, 1, 0, 0, 1])
# 事前分布(平均2のガンマ分布)
f_prev = gamma(a=6.0, scale=1.0/3.0)
x = np.linspace(0.0, 5.0, 100)
plt.plot(x, f_prev.pdf(x), 'b-', label='Prev')
# 事後分布
n = x_data.shape[0]
ap = np.sum(x_data)
print("observe {0} positive {1}".format(n, ap))
f_post = gamma(a=6.0+ap, scale=1.0/(3.0 + n))
plt.plot(x, f_post.pdf(x), 'r--', label='Post')
plt.legend()
Metropolis-Hastings法によるサンプリング
パラメータを$\theta$とする。現在の値$\theta^{(t)}$と、提案分布からサンプリングしてきた値$\theta_a$に対して、$\theta_a$を需要するかどうかを確率的に決定する。
$$
r = \frac{q(\theta^{(t)}\mid\theta_a) f(\theta_a\mid x)}{ q(\theta_a\mid\theta^{(t)}) f(\theta^{(t)}\mid x)}
$$
として、確率$r$で$\theta^{(t+1)}=\theta_a$と受容し、確率$1-r$で$\theta^{(t+1)}=\theta^{(t)}$として候補点を棄却する。
今回のポアソン分布とガンマ分布の場合、そもそも求めたい事後分布はベイズの法則より尤度と事前分布(例題ではパラメータα=11、λ=13のガンマ分布)の積に比例するので、$r$の式を変形して
$$
r = \frac{q(\theta^{(t)}\mid\theta_a) f(x\mid\theta_a) f(\theta_a)}{ q(\theta_a\mid\theta^{(t)}) f(x\mid \theta^{(t)}) f(\theta^{(t)})}
$$
とする。サンプルがi.i.d.と仮定すると尤度と事前分布は計算可能なので、M-H法を実装できる。
例えば提案分布として、平均が$\theta$ (与えられる)、分散が0.5の正規分布とする。
# データ
x_data = np.array([0, 1, 0, 0, 2, 0, 1, 0, 0, 1])
# 尤度
def log_likelihood(x, theta):
x_probs = poisson.pmf(x, theta)
return np.sum(np.log(x_probs))
# ガンマ分布のカーネル
def k_fg(theta, a, lbd): return np.exp(-lbd * theta) * (theta ** (a-1))
# 提案分布; 平均theta, 標準偏差0.5の正規分布
def q(x, theta): return sst.norm.pdf(x, loc=theta, scale=0.5)
# M-Hループ(初期値1.0、1000回)
def metropolis_raw(N):
current = 1.0 # 初期値
sample = []
sample.append(current)
for iter in range(N):
a = sst.norm.rvs(loc=prop_m, scale=prop_sd)
if a < 0: # reject (提案分布に
sample.append(sample[-1])
continue
T_next = q(current, a) * k_fg(a, a=11.0, lbd=13.0) * log_likelihood(x_data, a)
T_prev = q(a, current) * k_fg(current, a=11.0, lbd=13.0) * log_likelihood(x_data, current)
ratio = T_next / T_prev
if ratio < 0: # reject
sample.append(sample[-1])
if ratio > 1 or ratio > sst.uniform.rvs():
sample.append(a)
current = a
else:
sample.append(sample[-1])
return np.array(sample)
N = 10000
theta = metropolis_raw(N)
n_burn_in = 1000
# theta trace
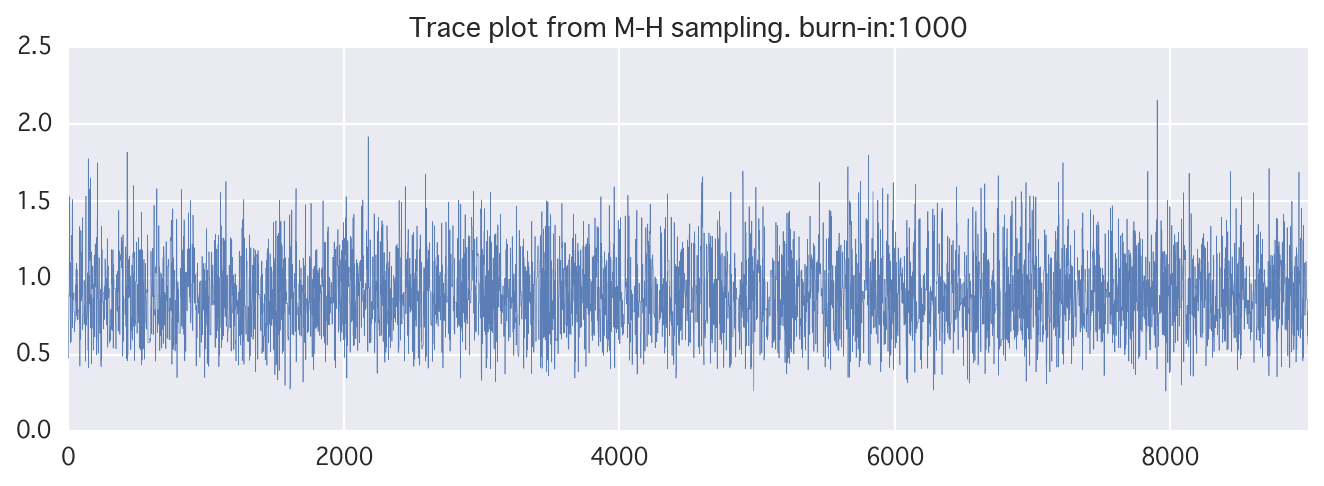
plt.figure(figsize=(10, 3))
plt.xlim(0, len(theta)-n_burn_in)
plt.title("Trace plot from M-H sampling. burn-in:{}".format(n_burn_in))
plt.plot(theta[n_burn_in:], alpha=0.9, lw=.3)
# plot samples
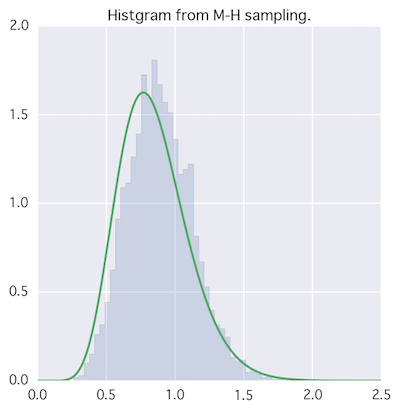
plt.figure(figsize=(5,5))
plt.title("Histgram from M-H sampling.")
plt.hist(theta[n_burn_in:], bins=50, normed=True, histtype='stepfilled', alpha=0.2)
xx = np.linspace(0, 2.5,501)
plt.plot(xx, sst.gamma(11.0, 0.0, 1/13.).pdf(xx))
plt.show()
実装が間違ってるのか、意外と良くない
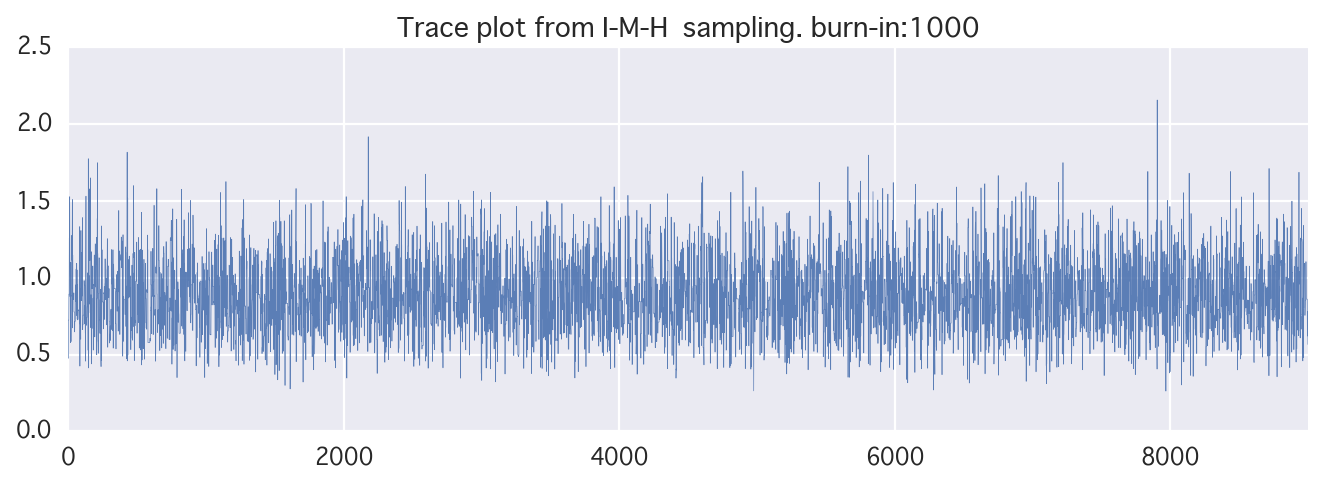
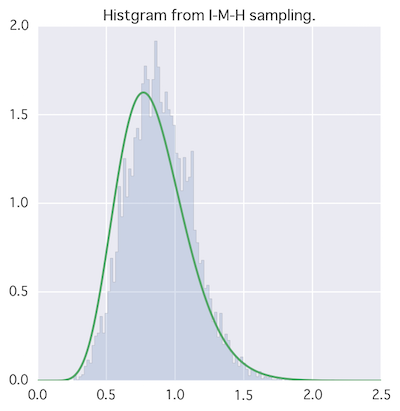
独立M-H法
上の例では正規分布(パラメータを与える)を提案分布にしていたけど、そもそもfとq独立でも良くない?→独立M-H法
import scipy.stats as sst
# 提案分布; 正規分布(パラメータ固定)
prop_m, prop_sd = 1.0, 0.5
def q(x): return sst.norm.pdf(x, loc=prop_m, scale=prop_sd)
# aとrの計算を置き換える
a = sst.norm.rvs(loc=prop_m, scale=prop_sd)
r = (q(current)*k_fg(a,a=11.0, lbd=13.0)) / (q(a)*k_fg(current,a=11.0,lbd=13.0))
実装が不安になってくる。
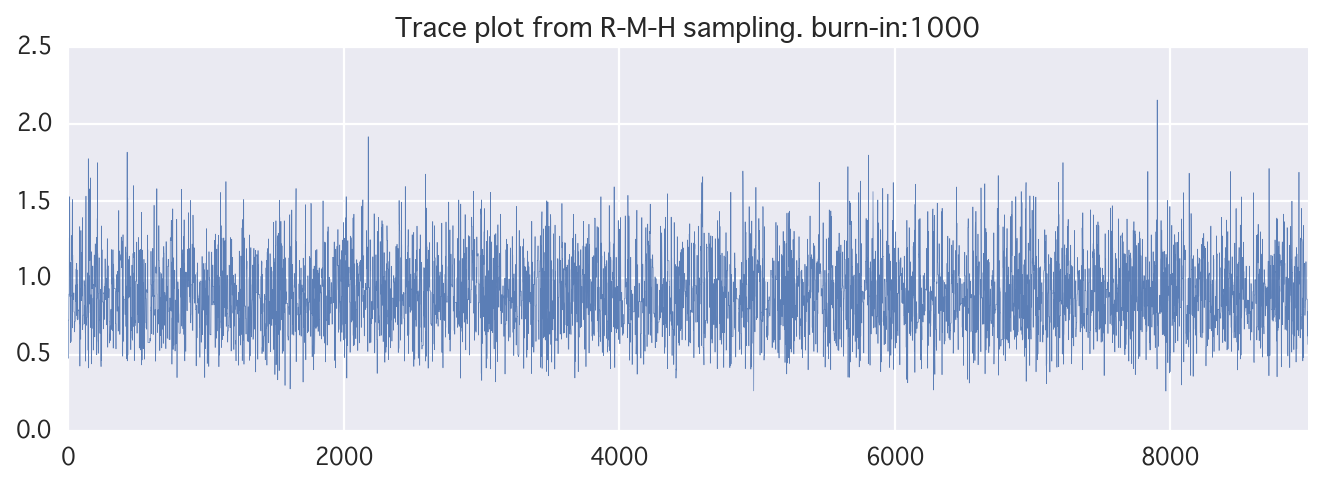
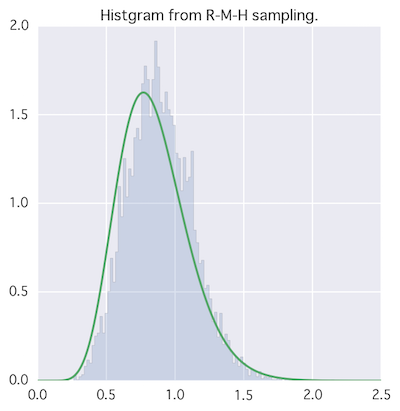
ランダムウォークM-H法
候補点をランダムウォークさせよう(直球)
→ 正規分布を使うと、平均に今までの提案値(a)、分散を適当に入れる。
current = 4.0
list_theta = []
list_theta.append(current)
# ランダムウォーク用(与えられたパラメータを平均にブレる)
def f_g(theta):
prop_sd = np.sqrt(0.1)
return sst.norm.rvs(loc=theta, scale=prop_sd)
### aとrの計算部分を置き換える
a = f_g(current)
r = f_gamma(a) / f_gamma(current)
反復回数増やすともう少しマシになります。
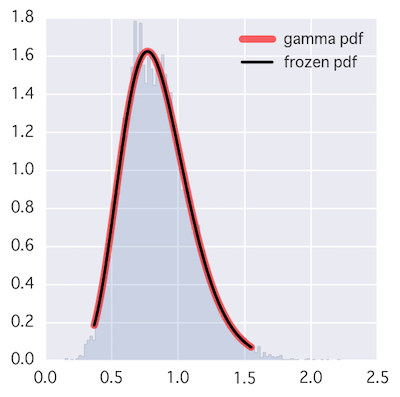
オマケ(scipyの関数)
本家のサンプリング能力。
import scipy.stats as sst
lbd = 1.0/13
plt.rcParams["figure.figsize"] = [4, 4]
a = 11.0
rv = sst.gamma(a, scale=lbd)
x = np.linspace(sst.gamma.ppf(0.01, a, scale=lbd), sst.gamma.ppf(0.99, a, scale=lbd), 100)
plt.plot(x, rv.pdf(x), 'r-', lw=5, alpha=0.6, label='gamma pdf')
plt.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')
vals = rv.ppf([0.001, 0.5, 0.999])
np.allclose([0.001, 0.5, 0.999], sst.gamma.cdf(vals, a, scale=lbd))
r = sst.gamma.rvs(a, scale=lbd,size=9000)
plt.hist(r, normed=True, bins=100, histtype='stepfilled', alpha=0.2)
plt.legend(loc='best', frameon=False)
HMC法
高校物理で、外部から力が加わっていない(他にも光とか熱で損失していない)ときに、力学的エネルギー(運動エネルギー+位置エネルギー)が保存されるよ、っていうのを習ったことがある人も多いはず。解析力学ではこれをハミルトニアンと読んで、一般化座標で議論する。それは置いとくとして(適当な解析力学の本を開くと最初の方にたぶん書いてある)、
$$
H(\tau) = U(\tau) + K(\tau)
$$
と書く。これだけだとサンプリングに何も関係はないけど、HMC法では事後分布$f(\theta\mid \mathbf{x})$からサンプリングするために、事後分布とは独立な標準正規分布$\mathcal{N}(p)$を持ってきて、同時分布$f(\theta, p\mid \mathbf{x}) = f(\theta\mid\mathbf{x})\mathcal{N}(p)$を考える。この同時分布からサンプリングしたときに、$\theta$には関係がない方を無視すれば、事後分布からサンプリングができたとする(ざっくりとしたイメージ)。
詳細は本に譲るとして、対数事後分布を$-h(\theta)$と置き、ハミルトニアンを$h(x)+\frac{1}{2}p^2$と計算して、次の手順でサンプリングする方法がHMC法です(1次元の場合)。
-
リープフロッグ法
のパラメータとして$\epsilon, L, T$を決める。 - 初期値 $\theta^{(0)}$ を決め、$i=0$とする(指定された$i$まで3〜6を繰り返す)
- 標準正規分布よりサンプルする … $p^{(i)} \sim \mathcal{N}(p^{(i)}\mid 0, 1)$
- リープフロッグ法により $\theta^{(i)}$ と $p^{(i)}$をLステップ変化させ、候補点 $\theta^{(a)}, p^{(a)}$ を計算する
- $r = \exp( H(\theta^{(t)}, p^{(t)}) - H(\theta^{(a)}, p^{(a)}))$として、確率 $\min(1, r)$ で5補店を受容し、それ以外では破棄する。
- t = t+1
実装して動作を見てみる。ポアソン分布-ガンマ分布のモデルで事後分布は正規化定数を除いて
$$
f(\theta\mid \mathbf{x}) \propto e^{- \lambda \theta} \theta^{\alpha -1}
$$
となるので、HMC法の$h(\theta)$とその微分は陽に計算できる(対数事後分布を計算して符号を反転させるとよい)。
# hとhの微分の定義
alpha, lbd = 11, 13
def _h(theta, alpha, lbd):
return lbd * theta - (alpha - 1) * np.ma.log(theta)
def _hp(theta, alpha, lbd):
return lbd - (alpha - 1) / theta
h = lambda theta: _h(theta, alpha, lbd)
hp = lambda theta: _hp(theta, alpha, lbd)
### ハミルトニアン
def H(theta, p):
return h(theta) + 0.5 * p * p
### リープフロッグ法の簡易実装
def lf(_th, _p, epsilon, L):
l_p = [_p]
l_th = [_th]
for tau in range(1, L):
p_t = l_p[-1]
theta_t = l_th[-1]
# 1/2
p_t_half = p_t - 0.5 * epsilon * hp(theta_t)
# update
next_theta = theta_t + epsilon * p_t_half
next_p = p_t_half - 0.5 * epsilon * hp(next_theta)
# store
l_p.append(next_p)
l_th.append(next_theta)
return (l_th[-1], l_p[-1])
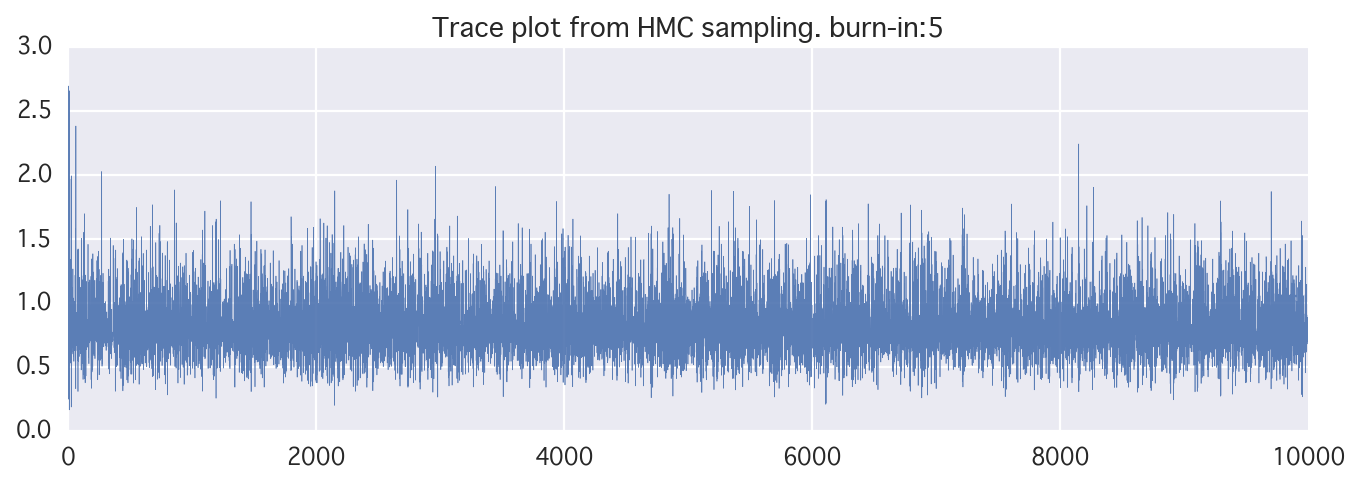
### HMCサンプリング
N = 10000
moves = []
theta = [2.5]
p = []
L = 100
epsilon = 0.01
for itr in range(N):
pv = sst.norm.rvs(loc=0, scale=1, size=1)[0]
p.append(pv)
# candidate by LF
curr_th, curr_p = theta[itr], p[itr]
cand_th, cand_p = lf(curr_th, curr_p, epsilon, L)
# compute r by exp(H(curr) - H(cand))
Hcurr = H(curr_th, curr_p)
Hcand = H(cand_th, cand_p)
r = np.exp(Hcurr - Hcand)
# print("{0}\t{1:2.4f}\t{2:2.4f}".format(itr, cand_th, cand_p))
# print("\t\t\t{0:2.3f}\t{1:2.3f}\t{2:2.3f}".format(Hcurr, Hcand, r))
if r < 0:
#reject
theta.append(theta[-1])
p.append(p[-1])
continue
if r >= 1 or r > sst.uniform.rvs():
theta.append(cand_th)
p.append(cand_p)
moves.append( (curr_th, cand_th, curr_p, cand_p) )
curr_th, curr_p = cand_th, cand_p
else:
#Reject
theta.append(theta[-1])
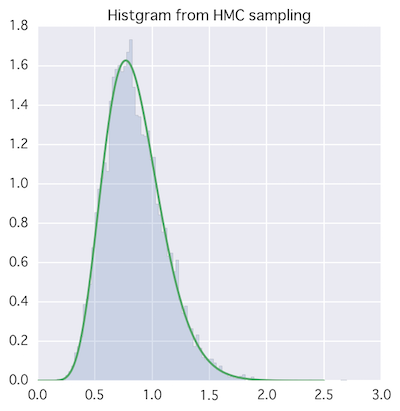
トレースとヒストグラムのプロット。
いい感じ。
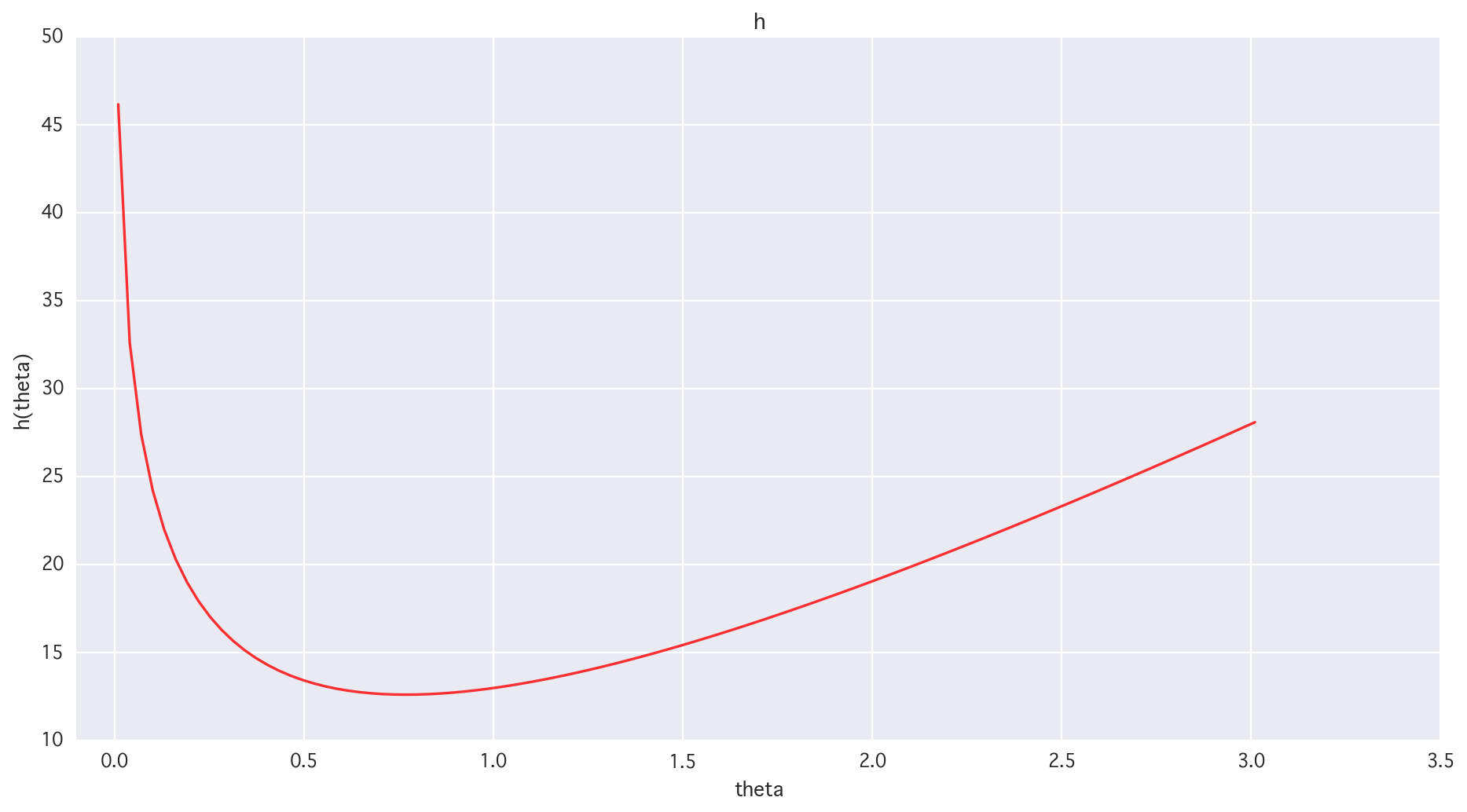
等高線とか描く
lin_p = np.linspace(-6.5, 6.5, 100.0)
lin_theta = np.linspace(0.01, 3.51, 100.0)
X, Y = np.meshgrid(lin_theta, lin_p)
Z = H(X, Y)
# 1dim h(theta)
xx = np.linspace(0.01, 3.01, 100)
plt.figure(figsize=(14, 7))
plt.title("h")
plt.plot(xx, h(xx), lw='1.5', alpha=0.8, color='r')
plt.xlim(-0.1, 3.5)
plt.xlabel("theta")
plt.ylabel("h(theta)")
# 2dim
plt.figure(figsize=(14,7))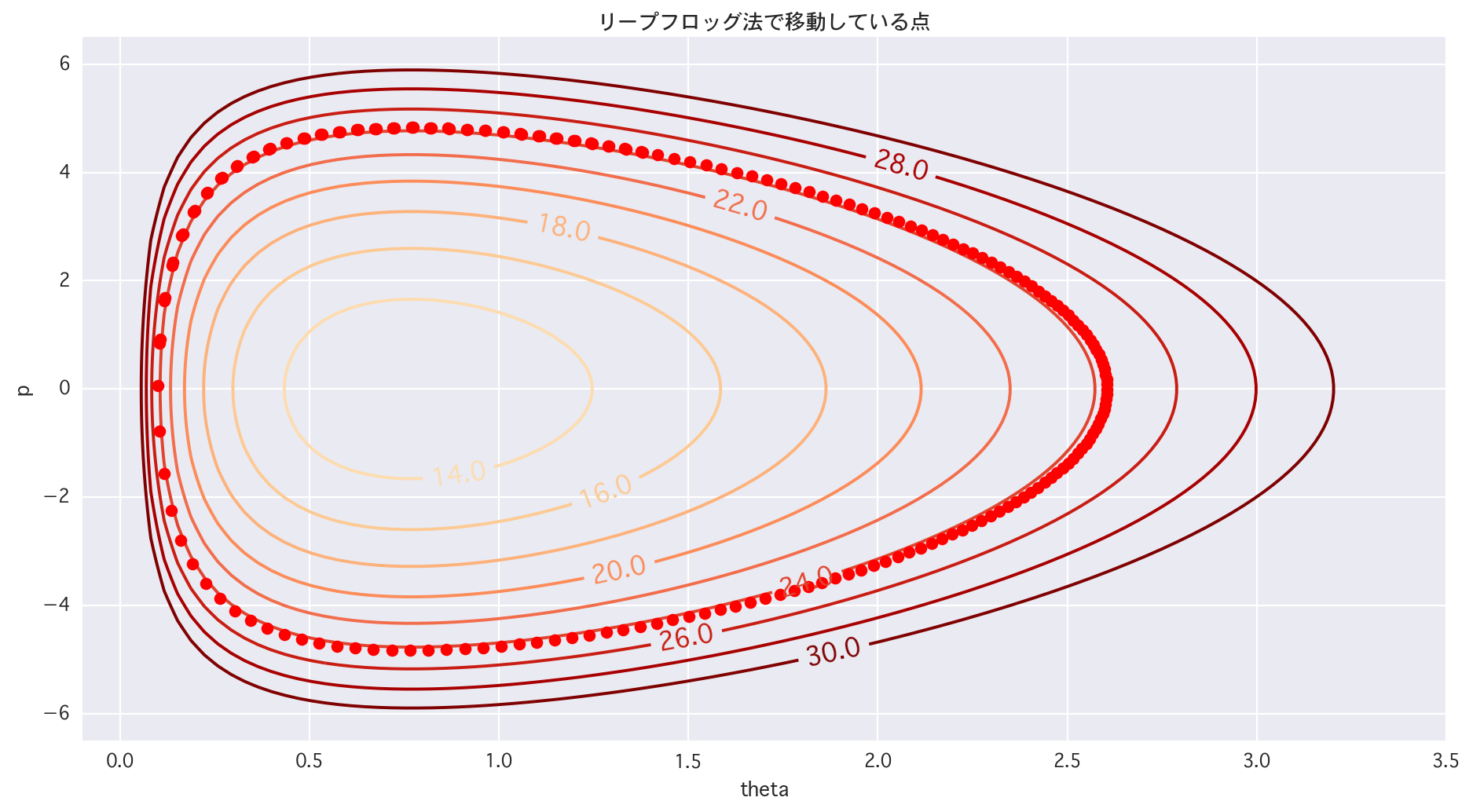
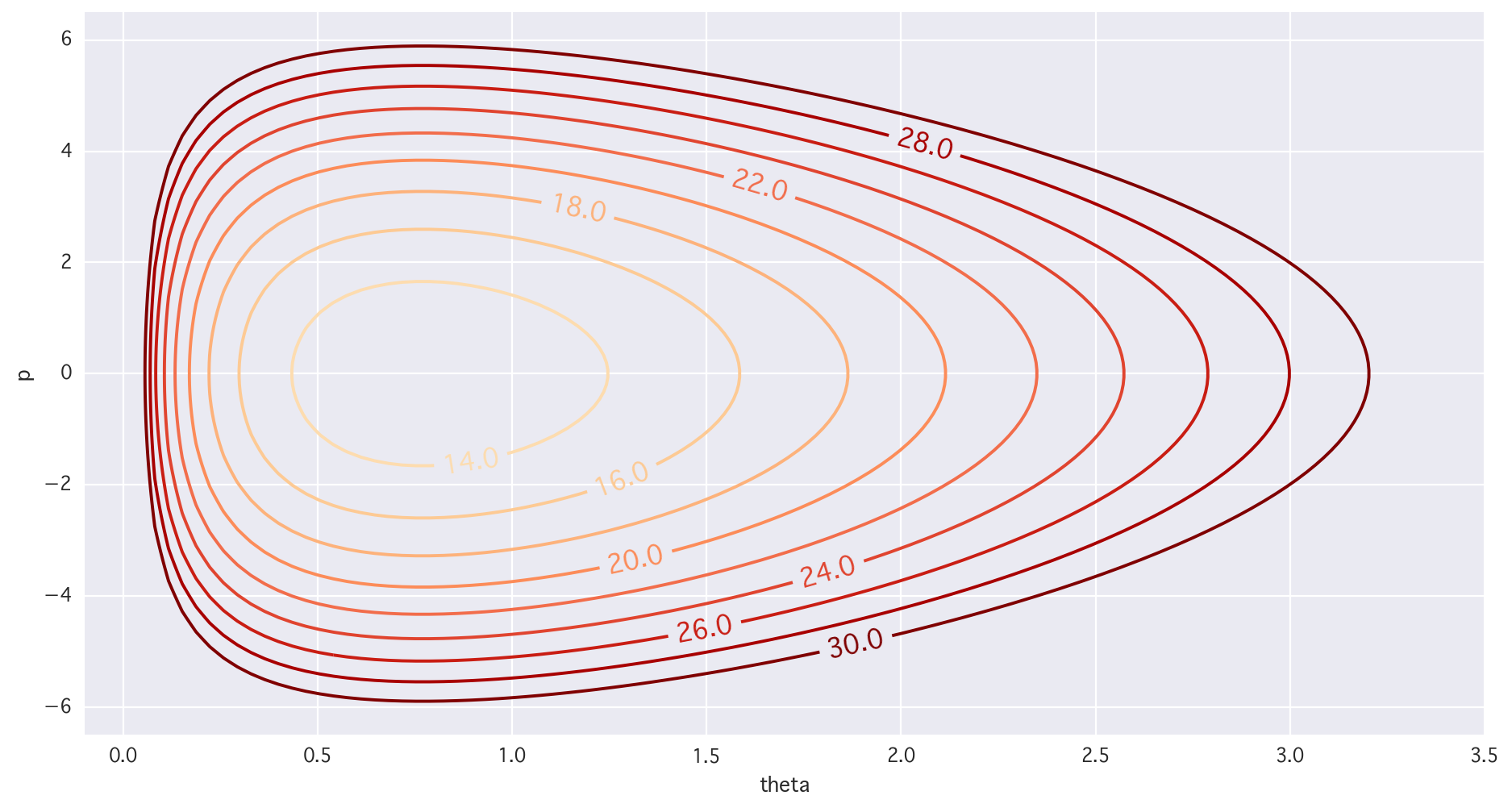
cont = plt.contour(X, Y, Z, levels=[i for i in range(10, 32, 2)], cmap="OrRd")
cont.clabel(fmt='%2.1f', fontsize=14)
plt.xlim(-0.1, 3.5); plt.ylim(-6.5, 6.5); plt.xlabel("theta"); plt.ylabel("p"); plt.show()
# 2dim (trace of LF)
# 1/4領域
plt.figure(figsize=(14,7))
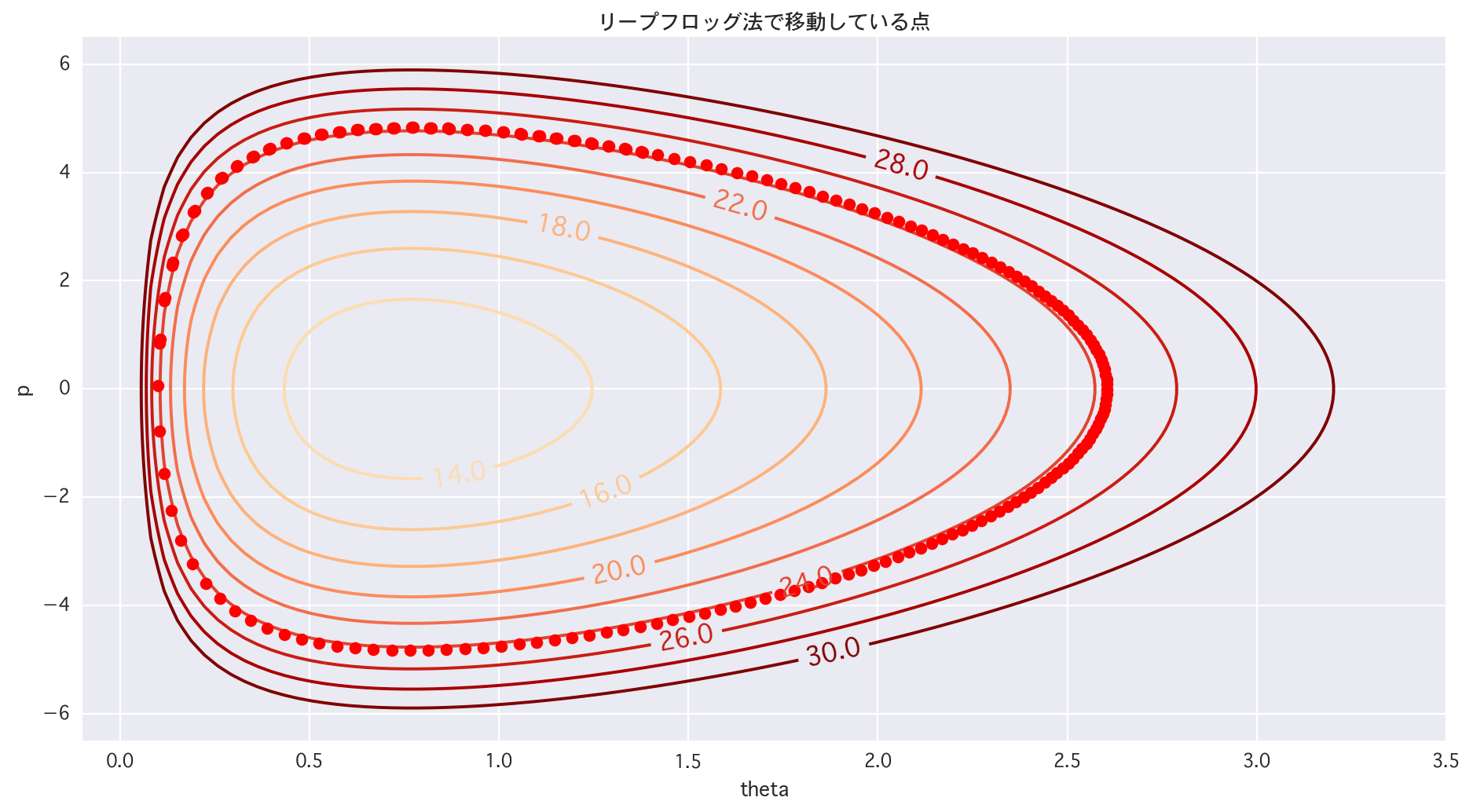
cont = plt.contour(X, Y, Z, levels=[i for i in range(10, 32, 2)], cmap="OrRd")
cont.clabel(fmt='%2.1f', fontsize=14)
for tau in range(1, len(p)):
plt.plot(theta[tau], p[tau], 'ro')
plt.title(u"リープフロッグ法で移動している点")
plt.xlim(-0.1, 3.5)
plt.ylim(-6.5, 6.5)
plt.xlabel("theta")
plt.ylabel("p")
plt.show()
Hamiltonianを保存したいという意思を感じる(適当)
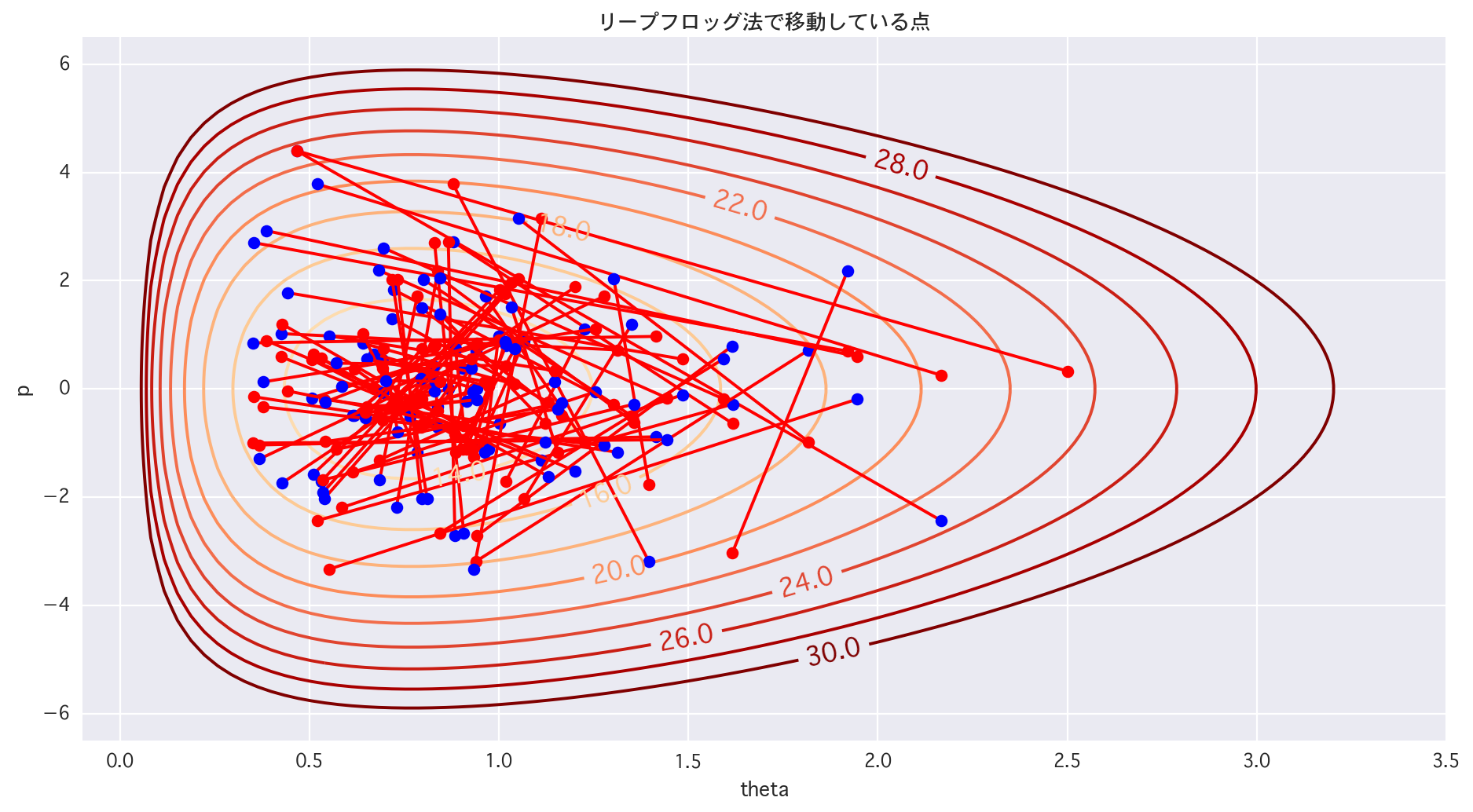
# どの点からどの点に飛んでいるか
# 1/4領域
plt.figure(figsize=(14,7))
cont = plt.contour(X, Y, Z, levels=[i for i in range(10, 32, 2)], cmap="OrRd")
cont.clabel(fmt='%2.1f', fontsize=14)
# for tau in range(1, len(p)):
# plt.plot(theta[tau], p[tau], 'ro')
plt.title(u"リープフロッグ法で移動している点")
plt.xlim(-0.1, 3.5)
plt.ylim(-6.5, 6.5)
plt.xlabel("theta")
plt.ylabel("p")
for i in range(len(moves)):
t0, t1, p0, p1 = moves[i][0], moves[i][1], moves[i][2], moves[i][3]
# plt.plot([t0, t1], [p0, p1], 'r-')
plt.plot([t0, t1], [p0, p1], 'r-')
plt.plot(t0, p0, 'ro')
plt.plot(t1, p1, 'bo')
plt.show()
実際に動かしてみると、学びが有ります。
予定
やり残したことは今年のうちに消化して更新します(フラグ)
- Slice Sampling
- NUTS