はじめに
私は現在大学4年生で、材料科学系の学科に所属しています。
材料科学系でも、機械学習はトレンドのようです。
機械学習の特徴量として、様々なパラメータが考えられますが、その中でも「形状を定量化するパーシステントホモロジーが有用なのではないか」というトピックがあります。
今回は、それをとりあえずやってみようという内容です。
本記事のプログラムは、次のColabのリンクから確認できます!
パーシステントホモロジー解析(PH解析)とは
PH解析の例として、シリカの例がよく用いられます。

左の点の集まりは、液体シリカとアモルファスシリカの原子配置の3Dマップです。
この点の集まりを見ても、どのような構造上の違いがあるのかわかりません。
しかし、それぞれPH解析すると、右のパーシステント図が得られます。
これをみると、何やら違いがあるように見えます。
これがPH解析です。
パーシステント図とは、どのような図なのかを説明します。
下図のように、4つの点の集まりを考えます。
- 点の周りに円を描きます。
- この円を大きくしていきます。
- r2で円で囲まれた「穴」ができます。
- r3で、穴が2つに分裂し、もうひとつ穴ができます。
- r4で、r3でできた穴が消滅します。
- r5になると、全ての穴が消滅します。
- 穴が誕生した半径(birth)を横軸に、穴が消滅した半径(death)を縦軸にプロットします。
これが1次のパーシステント図と呼ばれ、「穴」の構造を定量化されます。
白黒画像ではどう考えるか
この、シリカの点の集まりの例は比較的イメージしやすいですが、SEM像などの白黒画像ではどう考えればいいのでしょうか?
次のページの説明がわかりやすかったので引用します。
この下図のように、黒いピクセル部分を太らせていきます。
すると、白い部分の穴が誕生し、消滅します。

このようにして、白黒画像でもPH解析を行えます。
Colabで実行してみる
それでは、早速Colabで動かしてみましょう。
PH解析ツールは様々ありますが、HomCloudというツールを使用します。
HomCloudは、Colabでのチュートリアルがあり、とりあえず動かすのは簡単です。
HomCloudをColabにインストール
まずは、HomCloudをColabシステムにインストールします。
!apt-get install -qq libcgal-dev
!pip install -U numpy
!pip install Cython wheel
!pip install ripser
!pip install homcloud
!python -m homcloud.self_check
数分かかります。
次のセルで、ランタイムを再起動し、HomCloudを有効化します。
quit()
モジュールのインポート
ランタイムの再起動が終わったら、モジュールをインポートしましょう。
import os
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import imageio
from scipy.signal import argrelmin, argrelmax
import homcloud.interface as hc
画像の入力
画像の入力をしましょう。
input_image = "sample.png"
image_path = os.path.splitext(input_image)[0]
# mode="L" とするとグレースケールで読み込まれる
pict = imageio.v3.imread(input_image, mode="L")
画像の表示
入力した画像を表示してみましょう。
plt.imshow(pict, "gray")
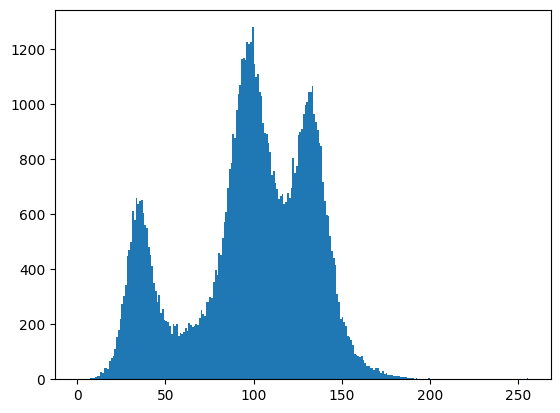
ヒストグラムの表示
輝度のヒストグラムを表示しましょう。
0が黒で、255が白です。
plt.hist(pict.ravel(), range=(0, 256), bins=256); None
今回は、山が3つあることがわかります。
閾値の設定
白黒画像をPH解析するには、白黒画像のまま解析する方法と、白黒画像に変換して解析する方法があります。
ヒストグラムに山が3つありましたが、今回は3相に分類してPH解析したいです。
そこで、ヒストグラムの谷の部分で区切って、相ごとに2値化して解析したいと思います。
SciPyに、極値を求める関数が用意してあるので、それを使って極小値(谷)を求め、そこで区切ることにします。
まず、ヒストグラムのデータを生成します。
histo, bins = np.histogram(pict.ravel(), range=(0,256), bins=256)
x=bins[1:]
y=histo
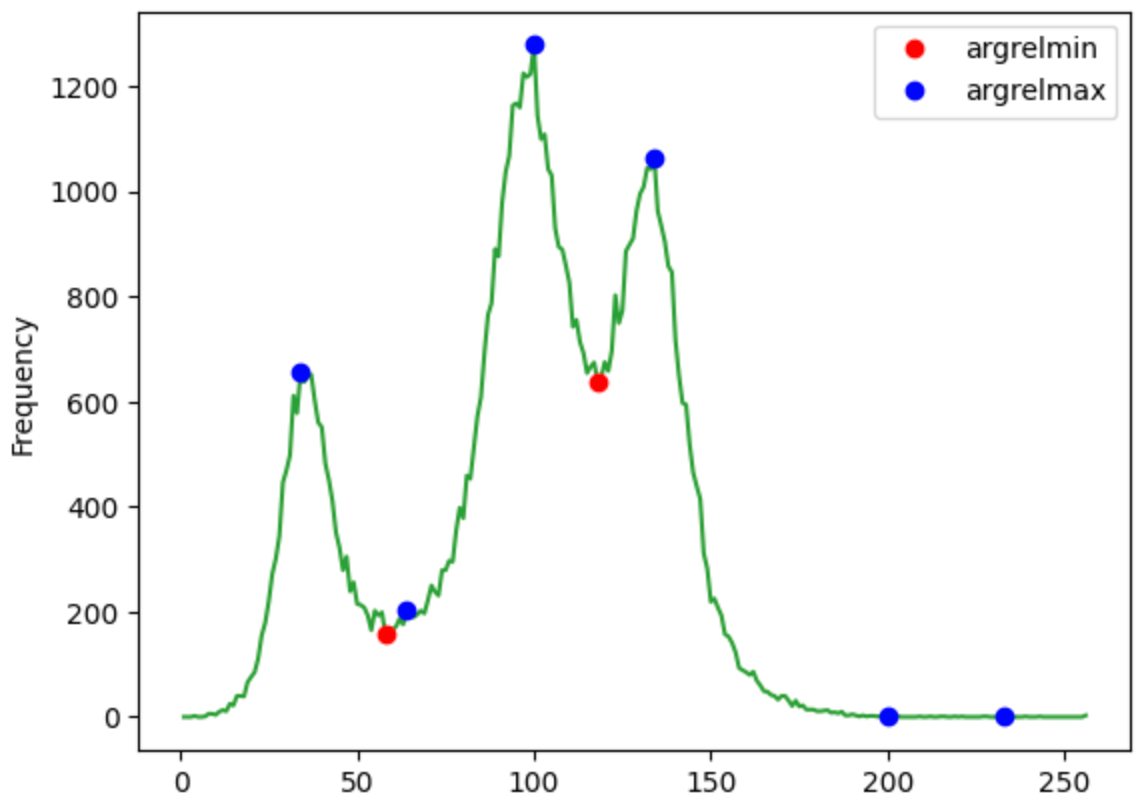
ヒストグラムのデータから、極値を求めます。
orderのパラメータを操作することで、ヒストグラムをどれくらいざっくり捉えるか?を調整できるみたいです。
デフォルトは1ですが、1ですと感度が良すぎます。
order = 1
arg_r_min,arg_r_max=argrelmin(y, order=order),argrelmax(y, order=order)
arg_r_min
極値をヒストグラム上に表示して確認します。
# 極値を表示
# figureとaxesを同時生成
fig, ax = plt.subplots()
# 第3引数はcolor cycle
ax.plot(x,y,"C2")
# 第2引数"ro"は、赤い点で表示の意味
ax.plot(x[arg_r_min[0]],y[arg_r_min[0]],"ro",label="argrelmin")
# 第2引数"bo"は、赤い点で表示の意味
ax.plot(x[arg_r_max[0]],y[arg_r_max[0]],"bo",label="argrelmax")
# 凡例
plt.legend()
# 軸ラベルを追加
ax.set(ylabel="Frequency")
# 保存
#plt.savefig("arg_rel_minmax2.png")
# 表示
plt.show()
orderを調整しましょう。
今回は、order=4としました。
order = 4
arg_r_min,arg_r_max=argrelmin(y, order=order),argrelmax(y, order=order)
arg_r_min
# 極値を表示
# figureとaxesを同時生成
fig, ax = plt.subplots()
# 第3引数はcolor cycle
ax.plot(x,y,"C2")
# 第2引数"ro"は、赤い点で表示の意味
ax.plot(x[arg_r_min[0]],y[arg_r_min[0]],"ro",label="argrelmin")
# 第2引数"bo"は、赤い点で表示の意味
ax.plot(x[arg_r_max[0]],y[arg_r_max[0]],"bo",label="argrelmax")
# 凡例
plt.legend()
# 軸ラベルを追加
ax.set(ylabel="Frequency")
# 保存
#plt.savefig("arg_rel_minmax2.png")
# 表示
plt.show()
2値化
取得した閾値を用いて2値化します。
pict_p1 = pict > arg_r_min_picked[0]
pict_p2 = (arg_r_min_picked[0] > pict) | (pict > arg_r_min_picked[1])
pict_p3 = arg_r_min_picked[1] > pict
2値化した後の画像を確認
2値化した後の画像を表示して確認してみましょう。
黒い部分が、解析したい部分です。
plt.imshow(pict_p1, "gray")
plt.imshow(pict_p2, "gray")
plt.imshow(pict_p3, "gray")
PH解析
2値化できたので、PH解析してみましょう。
hc.PDList.from_bitmap_levelset(hc.distance_transform(pict_p1, signed=True), save_to=image_path+"_p1.pdgm")
hc.PDList.from_bitmap_levelset(hc.distance_transform(pict_p2, signed=True), save_to=image_path+"_p2.pdgm")
hc.PDList.from_bitmap_levelset(hc.distance_transform(pict_p3, signed=True), save_to=image_path+"_p3.pdgm")
パーシステント図を表示
解析が終了したので、パーシステント図を表示してみましょう。
PH解析について説明した際、シリカの原子を太らせると話しました。
今回も同様で、着目している相(黒い部分)を太らせます。
ですので、シリカの例と同様に1次のパーシステント図を表示します。
dimensionの値を変えることで、何次のパーシステント図を取得するかを変えられす。
dimension = 1
pd_p1 = hc.PDList(image_path+"_p1.pdgm").dth_diagram(dimension)
pd_p2 = hc.PDList(image_path+"_p2.pdgm").dth_diagram(dimension)
pd_p3 = hc.PDList(image_path+"_p3.pdgm").dth_diagram(dimension)
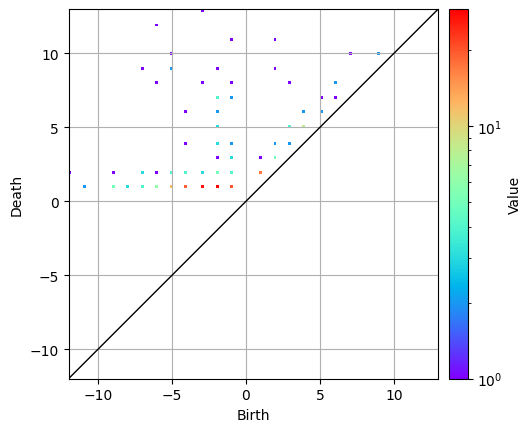
取得したパーシステント図を表示させましょう。
pd_p1.histogram().plot(colorbar={"type": "log"})
pd_p2.histogram().plot(colorbar={"type": "log"})
pd_p3.histogram().plot(colorbar={"type": "log"})
逆解析
パーシステント図を逆解析し、パーシステント図上の点が、白黒画像のどの部分に対応するのかを求めることができます。
逆解析
早速、逆解析をしましょう。
逆解析は次のコードで簡単に行えます。
hc.BitmapPHTrees.for_bitmap_levelset(hc.distance_transform(pict_p1, signed=True), save_to=image_path+"-tree_p1.pdgm")
hc.BitmapPHTrees.for_bitmap_levelset(hc.distance_transform(pict_p2, signed=True), save_to=image_path+"-tree_p2.pdgm")
hc.BitmapPHTrees.for_bitmap_levelset(hc.distance_transform(pict_p3, signed=True), save_to=image_path+"-tree_p3.pdgm")
1次のパーシステント図の逆解析結果を取得しましょう。
phtrees_p1 = hc.PDList(image_path+"-tree_p1.pdgm").bitmap_phtrees(dimension)
phtrees_p2 = hc.PDList(image_path+"-tree_p2.pdgm").bitmap_phtrees(dimension)
phtrees_p3 = hc.PDList(image_path+"-tree_p3.pdgm").bitmap_phtrees(dimension)
対角線から離れた部分の情報だけを取得
次に、対角線から離れた部分の情報だけを取得します。
対角線付近の成分は、ノイズ的な情報となります。つまり、対角線から離れた成分が重要ということです。
今回は、deathとbirthが5より離れた部分だけを取得します。
nodes_p1 = [node for node in phtrees_p1.nodes if node.lifetime() > 5 and node.death_time() != np.inf]
nodes_p2 = [node for node in phtrees_p2.nodes if node.lifetime() > 5 and node.death_time() != np.inf]
nodes_p3 = [node for node in phtrees_p3.nodes if node.lifetime() > 5 and node.death_time() != np.inf]
取得した逆解析結果を、白黒画像上に表示
取得した逆解析結果を、白黒画像上に表示することができます。
6つの引数を渡しています。それぞれの意味を確認しておきます。
- nodes_p1 : 取り出したノード
- input_image : 下地となる白黒画像
- color : 領域を色付けるための色。(R, G, B)で指定。今回は赤。
- alpha : 領域を色付けるためのアルファ値。透過度のこと。
- birth_position : birth positionの色
- marker_size : birth positionのマーカーサイズ
hc.draw_volumes_on_2d_image(nodes_p1, input_image, color=(255, 0, 0), alpha=0.2, birth_position=(255,0,0), marker_size=3)
hc.draw_volumes_on_2d_image(nodes_p2, input_image, color=(255, 0, 0), alpha=0.2, birth_position=(255,0,0), marker_size=3)
hc.draw_volumes_on_2d_image(nodes_p3, input_image, color=(255, 0, 0), alpha=0.2, birth_position=(255,0,0), marker_size=3)

それぞれ、2値化した画像の黒い部分の形状の情報が抽出できていることがわかります。
おわりに
ここまで読んでいただきありがとうございます。
本記事の内容がどなたかのお役に立てると嬉しいです。
いいねとストックお願いします!
本記事のプログラムは、次のColabのリンクから確認できます!