Juliaでグラフラプラシアンを用いた合意形成を計算する

内容

• グラフラプラシアンの固有値をプロットした
  • Juliaでグラフラプラシアンの固有値を求めて描画する - Qiita
• 例題のグラフラプラシアンに対応したグラフを参考に、最も簡単な合意形成を考えてみる

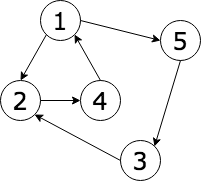
例題状況のグラフ

• 隣接行列 $A$ を図示すると以下の系が得られる

概要

• ノード数が5つなので、状態変数5つをベクトル化し $x = (x_1, x_2, x_3, x_4, x_5)$ と表す
• 状態変数 $x_i$ の時間変化は、自身の値と制御器（コントローラ）の入力を関数 $f$ によって処理した結果決定されると仮定する
  • $\frac{dx_i(t)}{dt} = f_i(x_i(t), u_i(t))$
• 制御器 $u_i$ は、自分自身の状態変数値 $x_i$ と、自分の近傍の状態変数値によって決定される関数とする
  • 例えば $u_1(t) = c(x_1(t), x_4(t))$
    • 時刻 $t$ におけるノード1への制御信号は、自分の状態値 $x_1$ と $A$ で規定される近傍からの状態値 $x_4$ によって決定する
• 合意形成
  • 制御器により$\lim_{t\to\infty} x_i(t) = \alpha$となる合意値$\alpha$を達成すること
  • 例えば $\alpha=\frac{1}{N} \sum_{i} x_{0i}$ であるとき、平均値合意である

グラフラプラシアンで表現される系

• 具体的なシステム $f, c$ について、以下の積分系を仮定する

  • $x_i(0) = x_{0i}$
  • $\frac{dx_i(t)}{dt} = u_i(t)$
  • $u_i(t) = -\sum_{j\in\mathcal{N}i} x_i(t) - x_j(t) $
    • i番目のノードの近傍$N_j$中のノードjに対する状態変数値の差分が制御信号として入力される

• 行列 $A$ とグラフラプラシアンを思い出す

• 上の積分系は $\frac{dx(t)}{dt} = -Lx(t)$ という行列形式で表される。

計算例

• 初期値として $x(t) = (1, 3, 5, 7, 9)$ を与える
• この系が合意を達成することを確認する
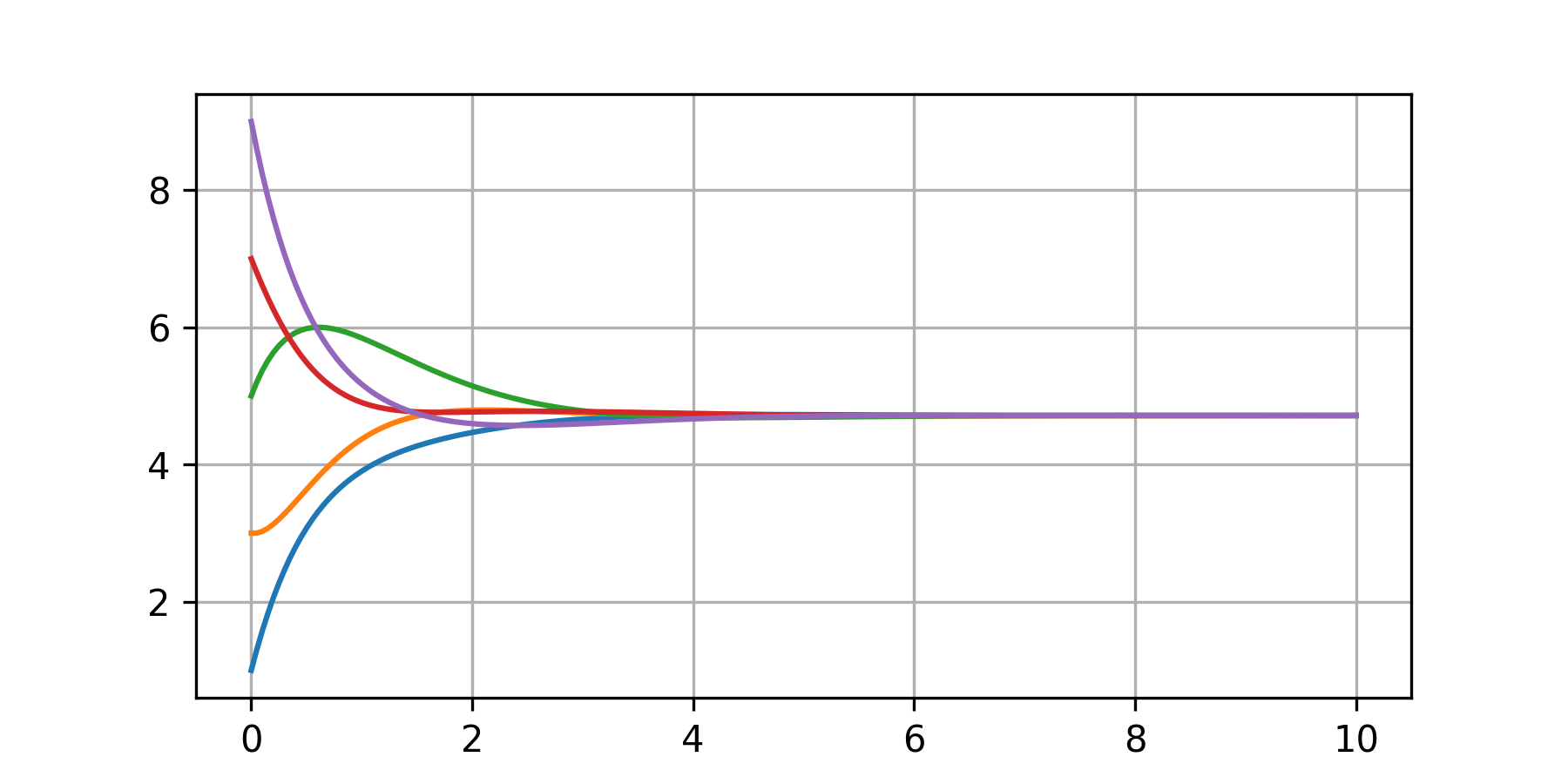
• 実行結果
  • 4.712程度の値に収束する（合意が形成される）

コード

using PyPlot

# 初期値
x = [1, 3, 5, 7, 9]

# グラフラプラシアンL
A = [0 0 0 1 0;
     1 0 1 0 0;
     0 0 0 0 1;
     0 1 0 0 0;
     1 0 0 0 0]
D = diagm(squeeze(sum(A, 2), 2))
Δ = maximum(D)
L = D - A

# シミュレーション
Δt = 0.05
tf = 10
xx = []
for t in 0:Δt:tf
    push!(xx, x)
    Δx = -L*x
    x += Δx * Δt
    print(x)
end

# plot
t = 0:Δt:tf
figure(figsize=(6, 3))
plot(t, xx)
grid(true)
savefig("ex3.png", format="png", dpi=300)