フィボナッチ数列とは?
フィボナッチ数列はプログラマにとっても馴染みあるものだと思います。1, 1 から始まって「前の二つを足して次の項を作っていく」ルールによって作られる数列です。
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...]
各項がその前の2項の和になっていますね。プログラマのスキルを試す問題として「フィボナッチ数列を関数として実装せよ」は定番ですよね。これは再帰呼び出しを使えば1行で書けます:
func fib(n: Int) -> Double {
return (n < 2) ? 1.0 : fib(n - 1) + fib(n - 2)
}
f(0) = 1, f(1) = 1 で、f(2) = f(1) + f(0) = 2, f(3) = f(2) + f(1) = 5 と次々求まって行くのが分かると思います。(このやり方だと関数呼び出しが 2^n のオーダーで膨れ上がるので実用上は値をキャッシュする必要があります)
フィボナッチ数列は数がどんどん足されて無限に大きくなっていきますが、この「増え方」には実は秩序があるのです。隣り合う項の比をとって見ると、
0: 1 / 1 = 1
1: 2 / 1 = 2
2: 3 / 2 = 1.5
3: 5 / 3 = 1.666...
...
という具合で、これを続けていけば:
4: 1.6
5: 1.625
6: 1.61538461538462
7: 1.61904761904762
8: 1.61764705882353
9: 1.61818181818182
10: 1.61797752808989
11: 1.61805555555556
12: 1.61802575107296
13: 1.61803713527851
14: 1.61803278688525
...
と、何やら 1.618... みたいな値に落ち着いていきそうです。実はこの極限は 黄金比 φ = 1.618033988749894... になるのです。
黄金比とは?
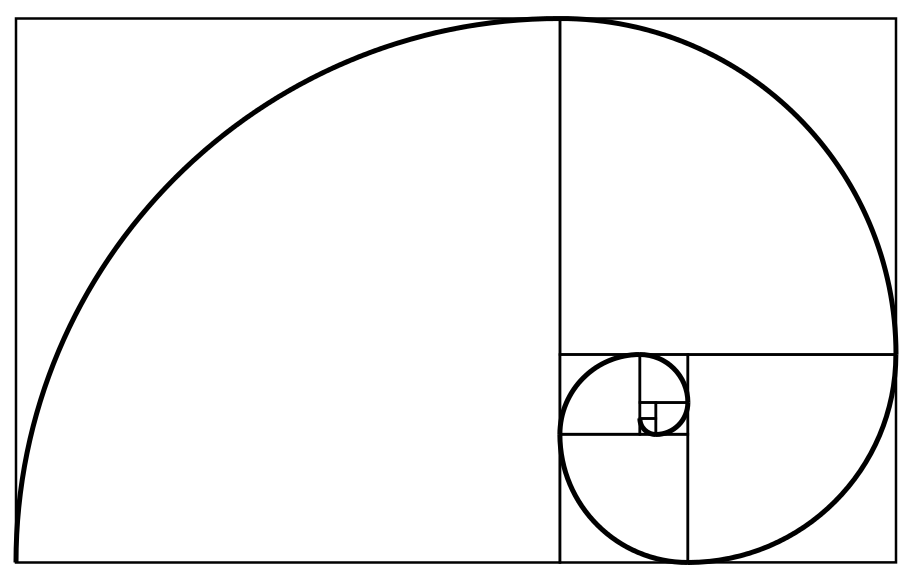
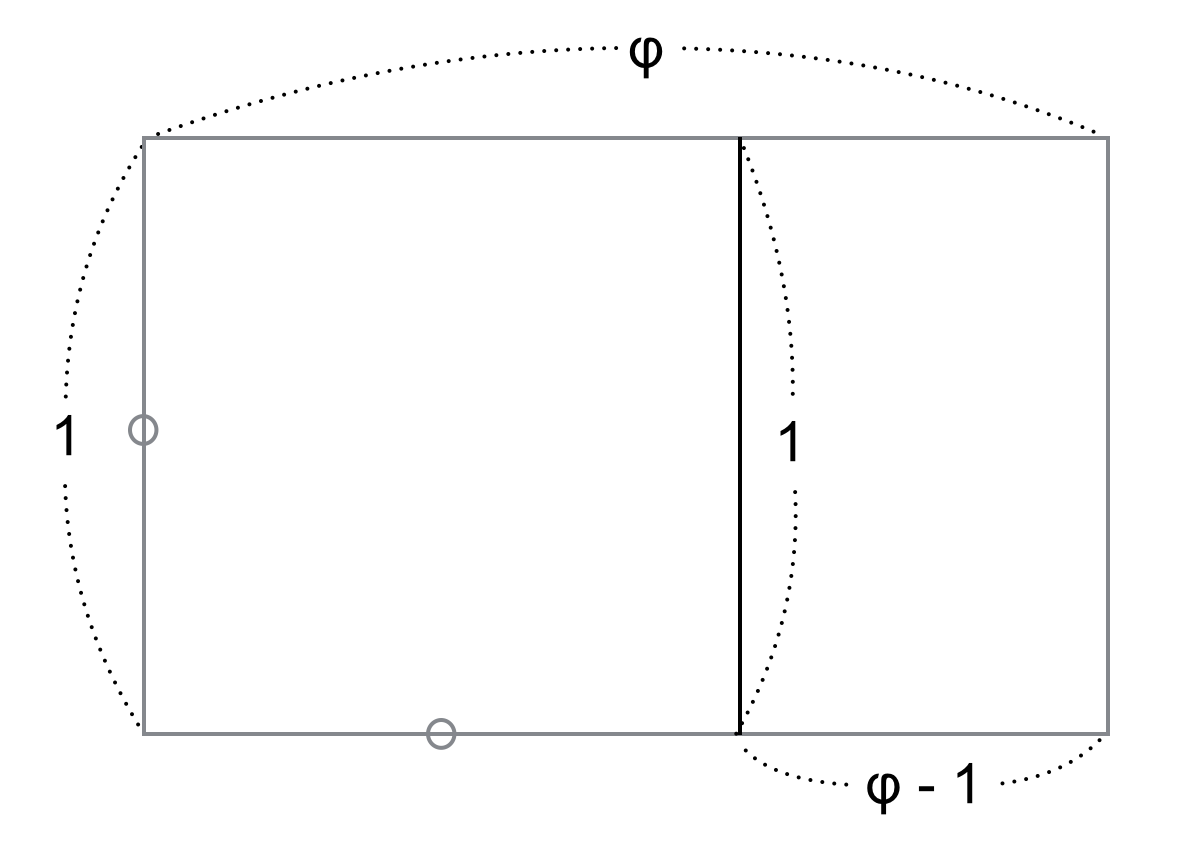
この図を見たことある方は多いでしょう。縦横の比が黄金比になっている長方形は、短辺側の正方形を取り除いても同じ比率の長方形が残るのが特徴です。
簡単な比の計算から黄金比 φ を求めることができます。
φ : 1 = 1 : φ - 1
から、
φ : 1 = 1 : φ - 1
φ(φ - 1) = 1 \Leftrightarrow φ^2 - φ - 1 = 0
という φ に関する2次方程式が得られ、解の公式から、
φ = \frac{1 \pm \sqrt{5}}{2}
と求まります。ここで $\pm$ と値が二つありますが、片方はマイナスになるので正の方が黄金比です。実際に計算してみると
(1.0 + sqrt(5)) / 2 // 1.618033988749895
となります。
フィボナッチ数列の比は黄金比へと近づいていく。このことは漸化式をいじって極限を取ることで示すこともできるのですが、もっと深くこの事実を洞察してその内奥に潜む構造を見てみることにしましょう。
フィボナッチ数列の一般化
まずフィボナッチ数列生成のルール:
a_{n+2} = a_{n+1} + a_n
は守りつつ、初期値は自由に取れるようにした「一般のフィボナッチ数列」を考えてみましょう。例えば数列を 3, -1 から始めることにすれば、「前の二つを足して次の項を作っていく」ルールによって、
3, -1, 2, 1, 3, 4, 7, 11, 18, 29, ...
が得られます。「一般のフィボナッチ数列」の実装は、初期値を数列の関数のパラメータに含めることで:
func fib(a0: Double, _ a1: Double, _ n: Int) -> Double {
switch n {
case 0: return a0
case 1: return a1
default: return fib(a0, a1, n - 1) + fib(a0, a1, n - 2)
}
}
とできますが、これだと上の数列は:
fib(3, -1, 0) // 3
fib(3, -1, 1) // -1
fib(3, -1, 2) // 2
fib(3, -1, 3) // 1
...
と書いていかねばならず、全然数列って感じがしません。オブジェクト指向であればここで「フィボナッチ数列クラスを作ってコンストラクタに初期値を…」となりますが、ここでは「関数型」のアプローチを取ってみましょう。こうです:
func Fib(a0: Double, _ a1: Double)(_ n: Int) -> Double {
switch n {
case 0: return a0
case 1: return a1
default: return Fib(a0, a1)(n - 1) + Fib(a0, a1)(n - 2)
}
}
さっきと何が変わったのでしょう? fib が大文字の Fib になって、2番目と3番目の引数がカッコで分離されただけです。ところがこうすることで:
let f = Fib(3, -1)
f(0) // 3
f(1) // -1
f(2) // 2
f(3) // 1
f(4) // 3
f(5) // 4
f(6) // 7
と、Fib に (3, -1) を与えることでそれを初期値とするフィボナッチ数列 f が得られたのです。この Fib は元の 3変数関数 fib の「カリー化」と呼ばれるもので、フィボナッチ数列(を表す関数)を返す関数(つまり高階関数)となります。
Fib はこう書いても同じです:
func Fib2(a0: Double, _ a1: Double) -> ((Int) -> Double) {
return { n in
let f = Fib2(a0, a1)
switch n {
case 0: return a0
case 1: return a1
default: return f(n - 1) + f(n - 2)
}
}
}
二つの初期値を取り、戻り値の型は「Int を引数にとって Double を返す関数」つまり数列です。Fib2 の中では、戻り値となる関数(クロージャ)を即座に返しています( { n in ... } の部分がクロージャです)。このクロージャの中身は元の3変数関数 fib とほぼ同じですね。
こうみると Fib はフィボナッチ数列の「コンストラクタ」のようなものだと思えるでしょう。「だったら最初からクラスでいいじゃないか」と思われるかと思いますが、まぁひとまずクラスのことは忘れてついてきてください。
数列はベクトルか?
さて Fib で作られる一般のフィボナッチ数列のうち、(1, 0) で始まるものと (0, 1) で始まるものの二つを取ってみます:
let e1 = Fib(1, 0)
let e2 = Fib(0, 1)
また普通のフィボナッチ数列 f = Fib(1, 1) も取り、その列を並べてみると:
e1: [1, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...]
e2: [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...]
f : [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...]
なんということでしょう、f = e1 + e2 になっているではありませんか!(縦に数字を足してみてください)さっきの f = Fib(3, -1) の場合はどうでしょう。e1, e2 をそれぞれ 3倍、-1倍 した数列を並れば、
3 * e1 : [3, 0, 3, 3, 6, 9, 15, 24, 39, 63, 102, ...]
-e2 : [0, -1, -1, -2, -3, -5, -8, -13, -21, -34, -55, ...]
f : [3, -1, 2, 1, 3, 4, 7, 11, 18, 29, 47, ...]
やはり f = 3 * e1 - e2 になっています!
今、形式的に関数を足したり定数倍したりしたような書き方をしましたが、実はこれも実装できちゃうのです。先に数列の型を定義しておきます。数列とは「自然数をとって実数を返す関数」であると見て:
typealias NumSeq = (Int) -> Double
次に数列同士の和を定義します。Swift では演算子のオーバーロードがサポートされているので、遠慮なく使っていきましょう:
func +(f: NumSeq, g: NumSeq) -> NumSeq {
return { f($0) + g($0) }
}
これはつまり、f + g という関数を、(f + g)(n) = f(n) + g(n) によって定義したということです。クロージャによって与えられた f, g を包み込んだ新しい関数を作っているわけです。 $0 は f + g に渡される n: Int を表しています。こうして「数列と数列の和」=「二つの関数から一つの関数を返す関数」が定義できました。
同様に実数倍も:
func *(a: Double, f: NumSeq) -> NumSeq {
return { a * f($0) }
}
と定義します。これで:
let f = Fib( 3, 4)
let g = Fib(-1, 3)
let h = f + g // Fib(2, 7) と同じ
のように、数列がただの2次元ベクトルのように扱えるようになりました( Fib を無視すればただの成分の和に見えますよね?)。もはや NumSeq の実体は関数であったことを忘れてしまいそうですが、
h(0) // 2
h(1) // 7
h(2) // 9
...
で、ちゃんと数列になっています。高校では数列とベクトルは全く別のものとして習ったと思いますが、ここではもう開き直って、「数列とは値を返す機能つきのベクトルだ!」と思うことにしましょう。
フィボナッチベクトルは黄金比の方向へ
話を戻せば「フィボナッチ数列の比の極限は黄金比」になることをみようというのでした。このことは数列をベクトルと見れば、(1, 1) を次々に進めていけば「黄金比の方向」へと向かっていくということなのです。
「次々進める」とはどういうことでしょう。ここで f = Fib(1, 1) に対して次のような変換を考えます:
f: [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...]
shift(f): [1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...]
上下をジグザグに見ていけば分かる通り、shift(f) は 「f の並びをひとつ手前にズラした形」になっています。これを分かりやすくかけば:
f: [f(0), f(1), f(2), f(3), f(4), f(5), f(6), ...]
shift(f): [f(1), f(2), f(3), f(4), f(5), f(6), f(7), ...]
となります。この shift(f) の方も数列で、n を与えれば「f における n + 1 番目の値」が返ってきます:
shift(f)(0) // = f(1) = 1
shift(f)(1) // = f(2) = 2
shift(f)(2) // = f(3) = 3
shift(f)(3) // = f(4) = 5
shift(f)(4) // = f(5) = 8
...
つまり shift(f) は「f をひとつ進めた数列」なのです(返ってくる値が手前にズレたということは、元の関数で入力を次に進めたものが返ってくるということです)。実装は数式の通りです:
func shift(s: NumSeq) -> NumSeq {
return { s($0 + 1) }
}
なぜこんなものを考えるかというと、フィボナッチ数列は最初の2項を並べたベクトルとして表現すると、2項目より先の様子が見えなくなります。そこで f を n 回 shift することで f(n), f(n + 1) が最初の2項にやって来るので、n 項目の値がベクトルとして見えるようになるというわけです。
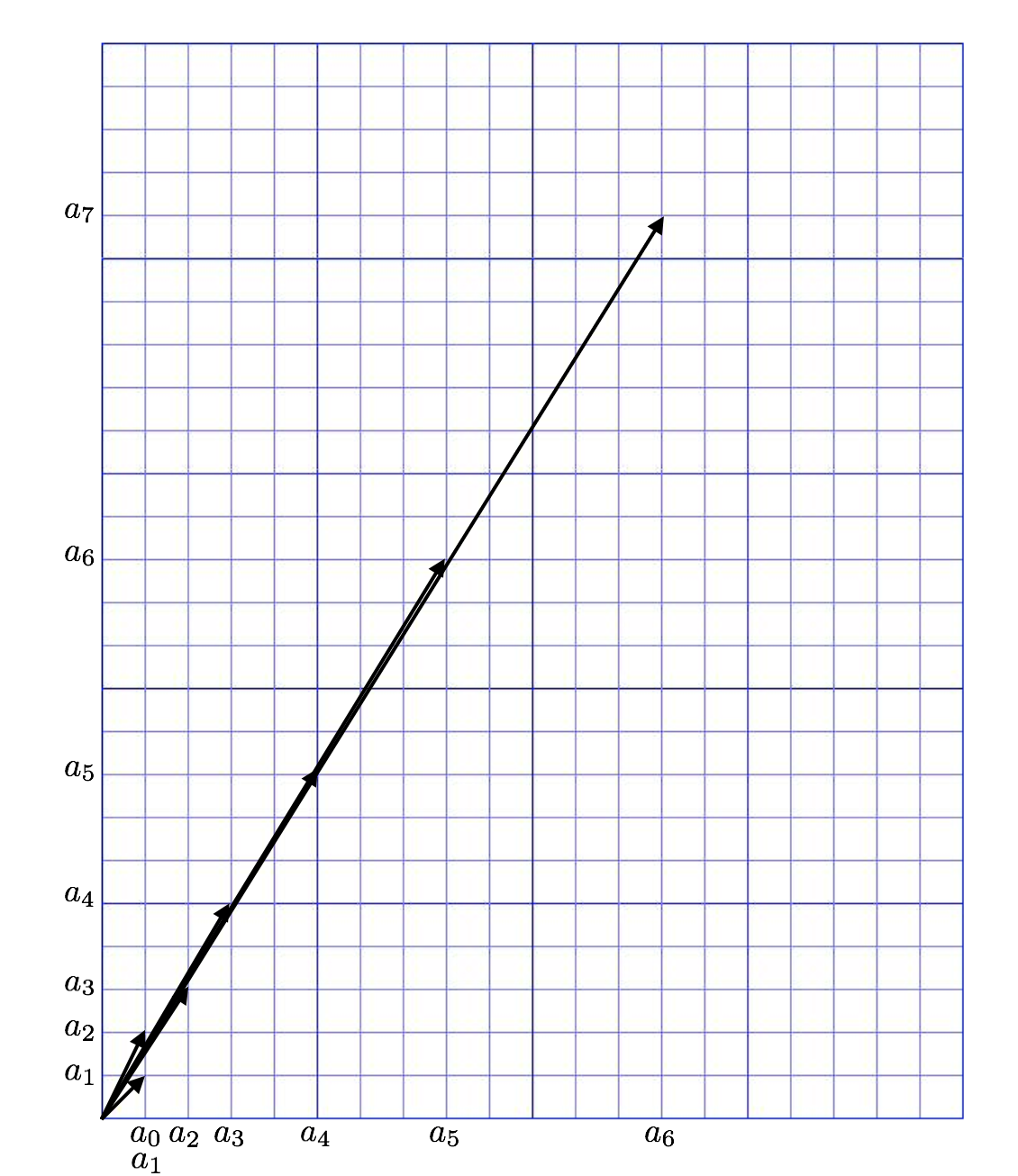
さて、フィボナッチ数列 (1, 1) に対して次々 shift を作用させた結果は次の通りです:
(1, 1) -> (1, 2) -> (2, 3) -> (3, 5) -> (5, 8) -> (8, 13) -> (13, 21) -> ...
もうお分かりの通り、このベクトルの傾きが f(n + 1) / f(n) で「フィボナッチ数列の比」です。「フィボナッチ数列の比の極限が黄金比」だということは、(1, 1) を次々 shift させて行けばどんどん黄金比の方向に進んでいくということです!
実際に計算してみると、
let f = Fib(1, 1)
let g = (shift^10)(f)
g(1) / g(0) // 1.617977528089888
となり、冒頭で求めた10番目の比の値と一致しています。10番目でもうこれだけ極限値に近いんですから、かなり収束が速いことが分かります。これでフィボナッチ数列の比が黄金比に向かっていく様子が想像できるようになったと思います!
※ ちなみに上の「n回合成する」という演算子 ^ は次のように実装しました(3次の高階関数):
func ^(F: (NumSeq -> NumSeq), k: Int) -> (NumSeq -> NumSeq) {
return (k == 0) ? {$0} : { (F^(k - 1))(F($0)) }
}
黄金等比数列
ところで、最初から「黄金比の方向」のフィボナッチ数列を取ったらどうでしょう。つまり (1, φ) を初期値として数列を作っていくのです:
let φ = (1.0 + sqrt(5)) / 2.0 // 1.618033988749895
let f = Fib(1, φ)
f(1) / f(0) // 1.618033988749895
f(2) / f(1) // 1.618033988749895
f(3) / f(2) // 1.618033988749895
f(4) / f(3) // 1.618033988749895
f(5) / f(4) // 1.618033988749895
...
極限を取るまでもなく、比は常に黄金比となっています。隣り合う項の比が一定の数列といえば…?そうです「等比数列」です。 (1, φ) から始まるフィボナッチ数列は、黄金比を公比とする等比数列になるのです!
より詳しく、公比 φ の等比数列は:
\{a_n\} = \{φ^n\} = \{1, φ, φ^2, φ^3, ...\}
と書けますが、これをフィボナッチ数列の漸化式:
a_{n+2} = a_{n+1} + a_n
に代入してみると:
φ^{n+2} = φ^{n+1} + φ^{n} \Leftrightarrow φ^2 = φ + 1
で、この式は長方形から黄金比を求めたときの2次方程式ではありませんか!逆に言えば黄金比とは、一般のフィボナッチ数列のうち、それが特別に等比数列となるときの公比だったわけです(もちろん普通のフィボナッチ数列を見れば分かる通り、一般にこの漸化式を満たす数列は等比数列にはなりません)
線形代数で種明かし
ここまで次々と式が出てきて何かうまく言いくるめられたように思われたかもしれないので、これまでの議論を線形代数の視点から解き明かしていきましょう。
まず「数列はベクトルだ」と言いましたが、これは数学的に全く正しい主張です。「一般のフィボナッチ数列全体」は、f1 = Fib(1, 0) と f2 = Fib(0, 1) を基底とする2次元のベクトル空間となります。数列空間は一般には有限次元とはならないのですが、この空間を定めていた漸化式:
a_{n+2} = a_{n+1} + a_n
によって、空間は2次元に制限されるのです。この漸化式が線形であるところがポイントで、定数項や2乗の項が入ってきたりすると上手くいきません。
次に shift という作用を考えましたが、これはこのベクトル空間における線形変換になっています。(1, 0), (0, 1) の移り先はそれぞれ (0, 1), (1, 1) なので、先ほどの基底に関する行列表示は:
A = \left(
\begin{array}{cc}
0 & 1 \\
1 & 1
\end{array}
\right)
です。この変換の固有方程式が:
\det(φI - A) = φ^2 - φ - 1 = 0
で、これは黄金比 φ を求めるときに出てきた方程式ですよね。つまり φ はフィボナッチ数列空間における線形変換 shift の固有値だったのです。この固有値に対する固有ベクトルは、
shift(f)(n) = f(n + 1) = φ \cdot f(n)
となるので、これはすなわち等比数列:
\{φ^n\} = \{1, φ, φ^2, φ^3, ...\}
です。もう一方の固有値は $\bar{φ} = 1 - φ$ で、その固有ベクトルは:
\{\bar{φ}^n\} = \{1, \bar{φ}, \bar{φ}^2, \bar{φ}^3, ...\}
です。こうして2つの1次独立な固有ベクトルが得られたので、これを新たな基底としてフィボナッチ数列を表せば、一般項:
a_n = \frac{φ^n - \bar{φ}^n}{\sqrt{5}}
が得られます( $a_0 = 0, a_1 = 1$ と取り直しました)。フィボナッチ数列は 0, 1, 1, 2, 3, 5, 8, ... と自然数が並ぶ列ですが、この一般項は分子にも分母にも思いっきり無理数が出てきているので不思議ですよね。 $φ$ と $\bar{φ}$ が絶妙のバランスで互いに打ち消しあって、自然数であることを保っているのです。またこの式を見れば、比の極限が黄金比に収束していくことも分かるはずです!
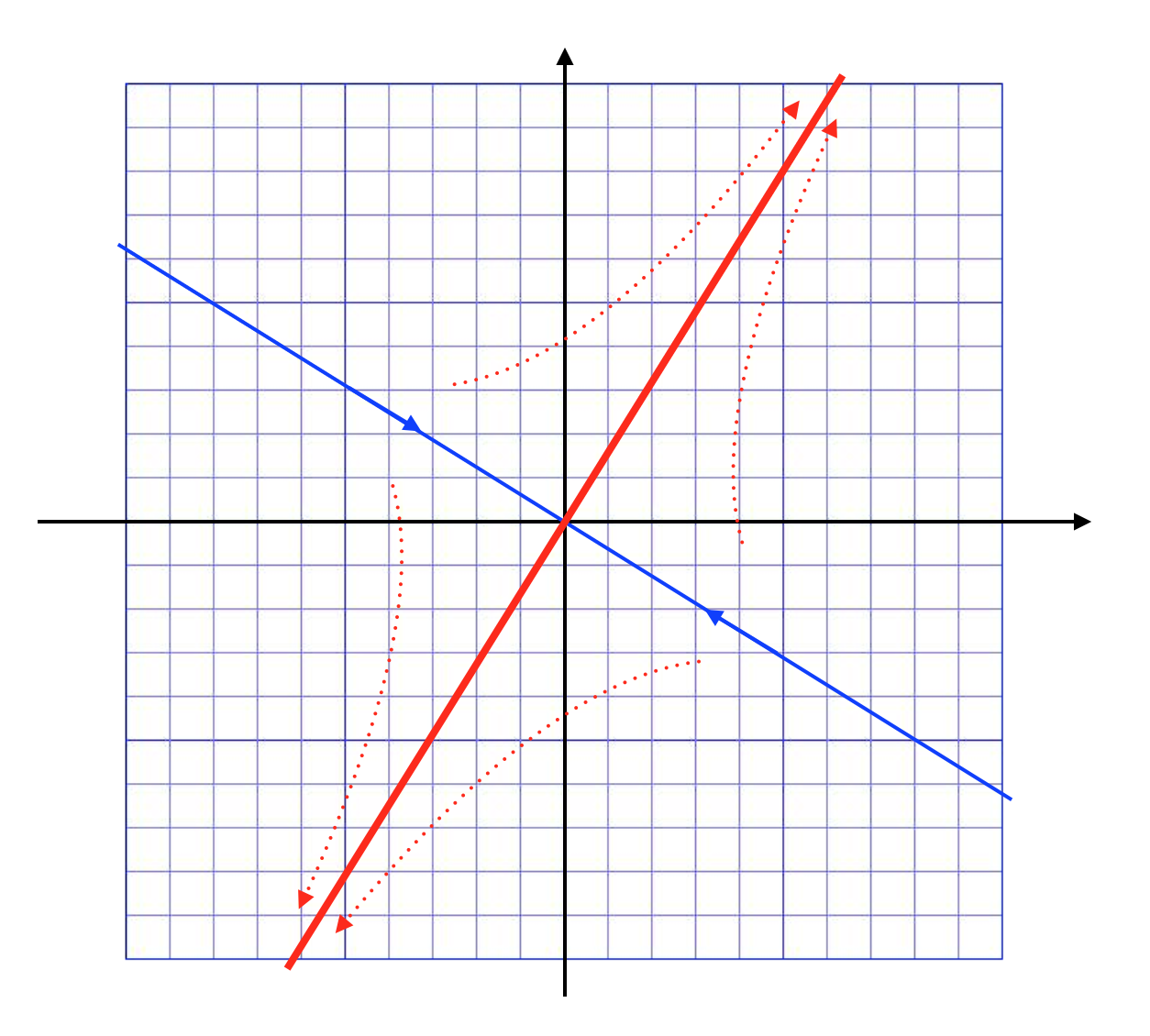
一般のフィボナッチ数列が shift によってどう進んでいくかを考えると、以下のような図が得られます。ほとんどの数列は黄金比の方向に進んでいくのですが、唯一それに直交する $(1, \bar{φ})$ の方向だけは shift のたびに振動しながら 0 に収束していきます。 shift が線形変換としてフィボナッチ数列空間に作用する様子が見えたでしょうか…!?
「種明かしどころか、何がなんだか全くわからん!」という方は、是非僕の「プログラマのための線形代数再入門」シリーズを見て、線形代数をもう一度勉強してみてください!(宣伝)
まとめ
数列を「自然数を取り実数値を返す関数」と定義し、そこに和や実数倍という演算を入れ、さらに shift という関数に対する作用を導入してその動きを見ていきました。
実際のコードではこのようなことはすべきでなく struct として数列型を定義した方がいいとは思いますが、数学における「関数空間」がプログラムにおける「関数」と対応する形で実装できるのは面白いかなと思い、敢えてこのような形にしてみました。
今回のサンプルコードはコチラです。さらに余力のある方は「トリボナッチ数列」で:
\begin{cases}
a_0 = 0, \ a_1 = 0, \ a_2 = 1 \\
a_{n+3} = a_{n+2} + a_{n+1} + a_{n} \\
\end{cases}
隣り合う項の比 $a_{n+1} / a_n$ がどうなるか調べてみましょう。以上 「フィボナッチ数列と線形代数」 でした!