こんにちは。大学の授業で学習した内容を忘備録もかねてqiitaに残していきたいと思います。
githubにサンプル・コードを載せてますので、参考になるかわかりませんが興味のある方は覗いて見ていただければと思います。
https://github.com/tkshim/MNIST/blob/master/BayesMNIST.py
-
内容:
・PCA(主成分分析)で特徴ベクトルの次元削減を行い、単純ベイズ分類器を使って、数字の画像認識を行う。 -
目的:
・機械学習を使ったコード(Python)の事例を共有する。 -
対象者:
・機械学習の基礎理論を理解しているが、他の人がコードでどうやって実装しているかサンプルをみたい。 -
環境:
・MacBook Air
・OSX 10.11.6
・Python 3.x
・numpy
・pandas
・sklearn -
まとめ:
・sklearnのビルトインのGaussianNBを使ったが、80%後半の正確性を出すことができた。
■step1
分析対象のデータセットはニューヨーク大学のルカン教授のホームページからダウンロード。http://yann.lecun.com/exdb/mnist/index.html
自分の環境に合わせて、データ置き場の変数を設定。
DATA_PATH = '/Users/takeshi/MNIST_data'
TRAIN_IMG_NAME = 'train-images.idx3-ubyte'
TRAIN_LBL_NAME = 'train-labels.idx1-ubyte'
TEST_IMG_NAME = 't10k-images.idx'
TEST_LBL_NAME = 't10k-labels.idx'
■step2, step3
学習、テスト用のデータセットをnumpyのアレイとして読み込む。
以下のようにimshowを使って各データがどの数字を表すのかを確認できます。
print("The shape of matrix is : ", Xtr.shape)
print("Label is : ", Ttr.shape)
plt.imshow(Xte[0].reshape(28, 28),interpolation='None', cmap=cm.gray)
show()
■step4
ここがPCAの心臓部分。画像データは28x28=784のデータで表されるのですが、この784個の特徴ベクトルをeigh関数を使って固有ベクトルを逆計算しています。
X = np.vstack((Xtr,Xte))
T = np.vstack((Ttr,Tte))
print (X.shape)
print (T.shape)
import numpy as np;
import numpy.linalg as LA;
μ=np.mean(X,axis=0);#print(μ);
Z=X-μ;#print(Z);
C=np.cov(Z,rowvar=False);#print(C);
[λ,V]=LA.eigh(C);#print(λ,'\n\n',V);
row=V[0,:];col=V[:,0];
np.dot(C,row)/(λ[0]*row) ;
np.dot(C,col)/(λ[0]*col);
λ=np.flipud(λ);V=np.flipud(V.T);
row=V[0,:];
np.dot(C,row)/(λ[0]*row);
P=np.dot(Z,V.T);#print(P);
*理論的な背景について知りたい方は以下の記事が参考になるかと思います。
http://postd.cc/a-beginners-guide-to-eigenvectors-pca-covariance-and-entropy/
■step5
784個ある固有ベクトル=主成分ですが、全て使うのではなく、例えば2個だけ使うことにして(=次元削減)、その2個の固有ベクトルをGaussianNBに適用することで、まずは認識モデルの完成です。
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
# Apply traing dataset to this model
# A: the number of training set
# B: the number of dimension
A = 60000
B = 2
model.fit(P[0:A,0:B],T[0:A])
■step6
固有ベクトルが2個の場合、テスト用データで正確性を検証してみると44.7%となり、かなり悪い数字になってしまいます。。
from sklearn import metrics
predicted = model.predict(P[A:70001,0:B])
expected = T[A:70001,]
print ('The accuracy is : ', metrics.accuracy_score(expected, predicted)*100, '%')
■step7
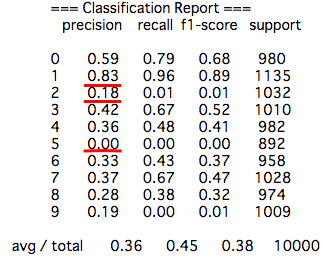
ここでは各数字の認識状況を確認できるようにClassification ReportやConfusion Matrixを表示させています。
import matplotlib.pyplot as plt
import seaborn as sns
print (' === Classification Report ===')
print (metrics.classification_report(expected, predicted))
cm = metrics.confusion_matrix(expected, predicted)
plt.figure(figsize=(9, 6))
sns.heatmap(cm, linewidths=.9,annot=True,fmt='g')
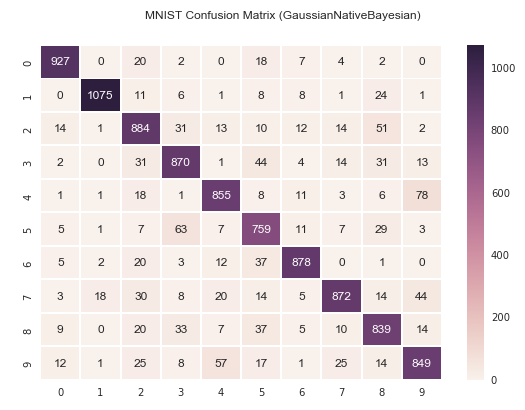
plt.suptitle('MNIST Confusion Matrix (GaussianNativeBayesian)')
plt.show()
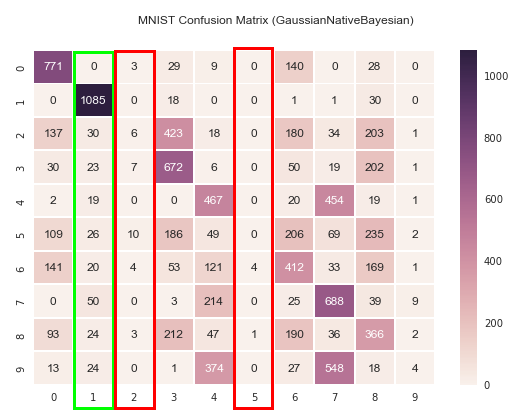
固有ベクトルが2の場合、数字の「1」は83%と悪くない一方で「2」や「5」がほとんど正しく認識されていないことが分かります。
なんでなのか?ということなのですが、これは、固有ベクトルが2個だけだと、数字によってはオーバーラップしてしまい、どの数字か判別が難しい場合があるためです。
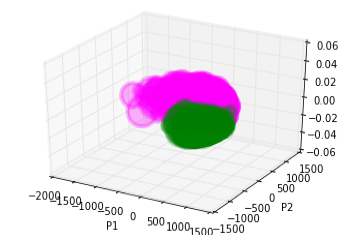
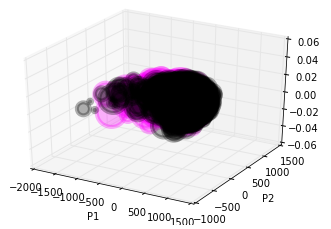
分かりやすい例で見てみましょう。上記のマトリックスでは、数字の4は数字の1と認識されるのは0回ですが、数字の9と誤認識されるのは374回あります。以下は数字の1と4の固有ベクトルを三次元にプロットした図です。1と4だと綺麗に固有ベクトルの集合が離れていることが分かります。しかし、4と9はどうでしょうか?ほとんどかぶっていてオーバーラップしてしまっています。
したがって、使用する固有ベクトルを徐々に大きくしてあげると正確性も向上して行きます。今回の環境では固有ベクトルを70前後に設定すると、正確性が最大化(80%後半)されるようです。
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
# Apply traing dataset to this model
# A: the number of training set
# B: the number of dimension
A = 60000
B = 70 # <-徐々に大きくする。
model.fit(P[0:A,0:B],T[0:A])
■固有ベクトル2と70での比較
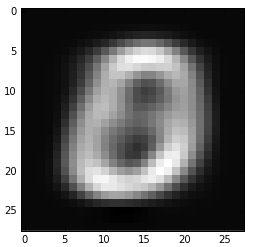
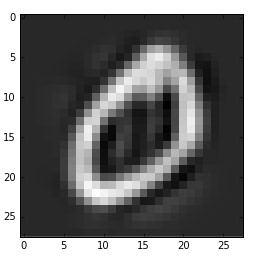
以下は固有ベクトルを2及び70として数字0を再現させた時の違いです。やはり、70にまで増やすとだいぶ輪郭がくっきりしてくることが分かります。
Xrec2=(np.dot(P[:,0:2],V[0:2,:]))+μ; #Reconstruction using 2 components
Xrec3=(np.dot(P[:,0:70],V[0:70,:]))+μ; #Reconstruction using 3 components
plt.imshow(Xrec2[1].reshape(28, 28),interpolation='None', cmap=cm.gray);
show()
plt.imshow(Xrec3[1].reshape(28, 28),interpolation='None', cmap=cm.gray);
show()
■まとめ
・Machine Learningの手法で80%後半の正確性を出すことができた。
・今回は、sklearnの単純ベイズ分類器を使っていますが、次回はこの分類器をPythonでスクラッチから実装し90%台を目指してみたいと思います。