State space (local level) model by stan

Library

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

import pystan

Data

path = '...'

m_return = pd.read_csv(path + 'monthly_return.csv')

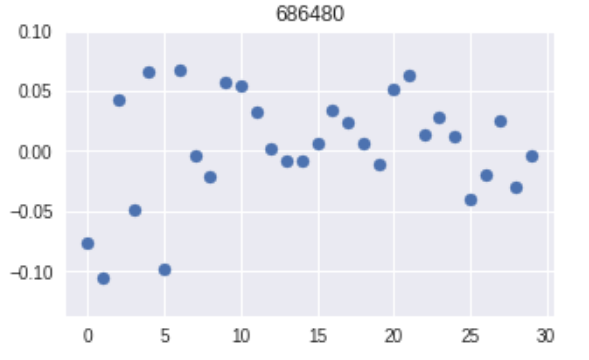
x = m_return['686480'][-30:].values.astype(float)

plt.figure(figsize = (5, 3))
plt.scatter(range(len(x)), x)
plt.title('686480')
plt.show()

Model

s_data = {'n': len(x), 'x': x}

s_code = """
  data {
    int n; 
    real x[n]; 
  }
  parameters {
    real mu_zero;      
    real mu[n];   
    real<lower=0> sig_v;  # observation
    real<lower=0> sig_w;  # state
  }
  model {
    # initial state
    mu[1] ~ normal(mu_zero, sqrt(sig_w));  

    # state 
    for(i in 2:n) {
      mu[i] ~ normal(mu[i-1], sqrt(sig_w));
    }

    # observation
    for(i in 1:n) {
      x[i] ~ normal(mu[i], sqrt(sig_v));
    }
  }
"""  

stm = pystan.StanModel(model_code=s_code)

n_itr = 2000
n_warmup = 1000
chains = 3

fit = stm.sampling(data=s_data, iter=n_itr, chains=chains, n_jobs=-1, 
                   warmup=n_warmup, algorithm="NUTS", verbose=False)

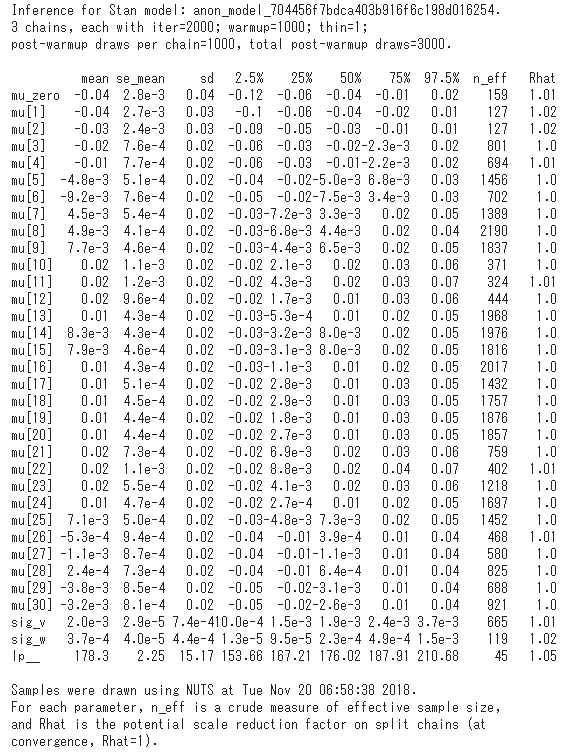
fit

eap = fit.summary()['summary'][1:31, 0]
lower95 = fit.summary()['summary'][1:31, 3] 
upper95 = fit.summary()['summary'][1:31, 7] 

print ('mean of mu: ')
print (eap)
print ()
print ('2.5% of mu:')
print (lower95)
print ()
print ('97.5% of mu:')
print (upper95)

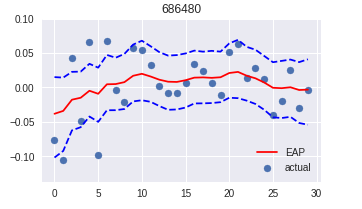
plt.figure(figsize = (5, 3))
plt.scatter(range(len(x)), x, label='actual')
plt.plot(eap, 'r', label='EAP')
plt.plot(lower95, 'b--')
plt.plot(upper95, 'b--')
plt.title('686480')
plt.legend(loc='best')
plt.show()