こんにちは。takepiyoです。今回は地磁気センサを使用して、yaw角に対しても拡張カルマンフィルタを適用してみました。結論から言うと、ヨー角のドリフト誤差を抑えることができました。
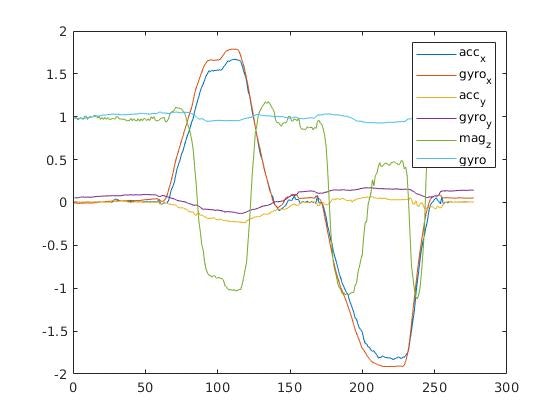
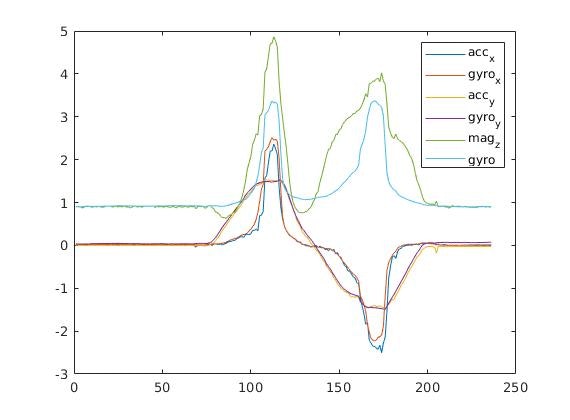
しかし、ヨー角を固定したまま、ロール角またはピッチ角を変化させた時にヨー角が変化してしまうという現象が起きてしまいうまく推定することができませんでした。
今回はそれも含めての記録とさせていただきます。
値磁気センサの準備
https://wiki.seeedstudio.com/Grove-3-Axis_Digitial_Compass_v2.0/
これを購入して、arduino用のライブラリをmbed仕様に修正して使用します。
https://os.mbed.com/users/takepiyo/code/bmm150/
Low power presetでは使い物にならなかったので、High accuracy preset で使用します。
キャリブレーション
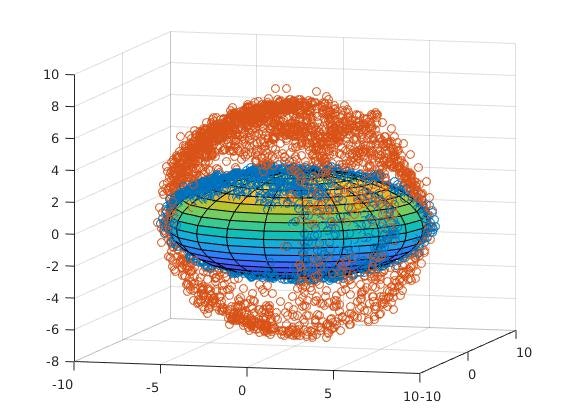
地磁気センサをつけたドローンをぐるぐる回して、センサの値を記録し、matlabで楕円体近似を行います。回転は考慮しない6自由度で計算を行いました。
sigma_x = sum(x);
sigma_y = sum(y);
sigma_z = sum(z);
sigma_x2 = sum(x.^2);
sigma_y2 = sum(y.^2);
sigma_z2 = sum(z.^2);
sigma_x3 = sum(x.^3);
sigma_y3 = sum(y.^3);
sigma_z3 = sum(z.^3);
sigma_x4 = sum(x.^4);
sigma_y4 = sum(y.^4);
sigma_z4 = sum(z.^4);
sigma_x_y = dot(x,y);
sigma_x_z = dot(x,z);
sigma_y_z = dot(y,z);
sigma_x2_y2 = dot(x.^2,y.^2);
sigma_x2_z2 = dot(x.^2,z.^2);
sigma_y2_z2 = dot(y.^2,z.^2);
sigma_x2_y = dot(x.^2,y);
sigma_x2_z = dot(x.^2,z);
sigma_y2_z = dot(y.^2,z);
sigma_y2_x = dot(y.^2,x);
sigma_z2_x = dot(z.^2,x);
sigma_z2_y = dot(z.^2,y);
jacov = [sigma_x4 sigma_x2_y2 sigma_x2_z2 sigma_x3 sigma_x2_y sigma_x2_z ;
sigma_x2_y2 sigma_y4 sigma_y2_z2 sigma_y2_x sigma_y3 sigma_y2_z ;
sigma_x2_z2 sigma_y2_z2 sigma_z4 sigma_z2_x sigma_z2_y sigma_z3 ;
sigma_x3 sigma_y2_x sigma_z2_x sigma_x2 sigma_x_y sigma_x_z ;
sigma_x2_y sigma_y3 sigma_z2_y sigma_x_y sigma_y2 sigma_y_z ;
sigma_x2_z sigma_y2_z sigma_z3 sigma_x_z sigma_y_z sigma_z2];
b = [sigma_x2; sigma_y2; sigma_z2; sigma_x; sigma_y; sigma_z];
kai = inv(jacov) * b;
f = @(X,Y,Z) kai(1) * X.^2 + kai(2) * Y.^2 + kai(3) * Z.^2 + kai(4) * X + kai(5) * Y + kai(6) * Z - 1;
% fimplicit3(f);
cen_left = [2 * kai(1) 0 0; 0 2 * kai(2) 0; 0 0 2 * kai(3)];
cen_right = [-kai(4); -kai(5); -kai(6)];
a
xc = -kai(4) / (2 * kai(1));
yc = -kai(5) / (2 * kai(2));
zc = -kai(6) / (2 * kai(3));
Z = 1 + (kai(4)^2 / kai(1) + kai(5)^2 / kai(2) + kai(6)^2 / kai(3)) / 4;
xr = sqrt(Z / kai(1));
yr = sqrt(Z / kai(2));
zr = sqrt(Z / kai(3));
[x_ellip,y_ellip,z_ellip] = ellipsoid(xc,yc,zc,xr,yr,zr);
figure
surf(x_ellip,y_ellip,z_ellip);
hold on
scatter3(x,y,z)
scatter3(x - xc,(y - yc) * xr / yr, (z - zc) * xr / zr);
青い点がもとの地磁気センサの出力で、それの楕円体近似と、球面への変換を行っています。(赤い点)
この赤い点のデータを使用してyaw角を推定します。
センサの観測方程式
補正された地磁気センサの値を$(d_x, d_y, d_z)$とし、
x,y,z周りの回転角度をそれぞれ $\phi, \theta, \psi$としたとき、北を0としたyaw角の回転角度は
\begin{bmatrix}
\phi \\
\theta \\
\psi
\end{bmatrix}
=
\begin{bmatrix}
\tan^{-1}\frac{a_y}{a_z} \\
-\tan^{-1}\frac{a_x}{\sqrt{a_y^2+a_z^2}} \\
\tan^{-1}(- \frac{\cos\phi d_y - \sin\phi d_z}{\cos\theta d_x + \sin\theta \sin\phi d_y + \sin\theta \cos\phi d_z})
\end{bmatrix}
実測値
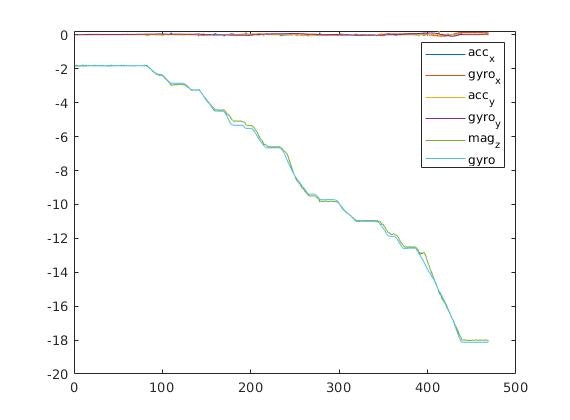
この観測方程式を用いて得られるオイラー角とジャイロセンサーから得られたオイラー角は以下のようになります。
-
ヨー角のみを変化させた場合
-
ロール角のみ変化させた場合
ヨー角が正しく観測できていない(水色と黄緑) -
ピッチ角のみ変化させた場合
ヨー角がかなり大きく観測されてしまったり、ロール角が変化してしまったりしている
ピッチ角の変化はオイラー角の特異点に関係するので、おかしくなっても仕方ないとは思いますが。
このようにうまく行かない原因がオイラー角の特異点に関することなのかを確認するために、次回はクォータニオンを状態量とした拡張カルマンフィルタを実装します。
もしこのような現象(特にロール角を変化させた時にヨー角が変化してしまうやつ)の原因をご存知、もしくは何か思い当たる人がいましたら、コメントにてご享受していただけますと嬉しいです。
ここまで読んで頂きありがとうございました。
参考
https://www.jstage.jst.go.jp/article/sposun/22/2/22_255/_pdf/-char/en
https://www.analog.com/media/jp/analog-dialogue/volume-53/number-1/strapdown-inertial-navigation-system-based-on-an-imu-and-a-geomagnetic-sensor_jp.pdf
https://www.jstage.jst.go.jp/article/jje/50/4/50_182/_pdf
ドローン制御工学入門
https://watako-lab.com/2019/02/20/3axis_cmps/