この記事の目的
再帰という方法があります。
再帰とは、「関数が、その関数内で、自分自身を呼び出す」というようなものです。
Tree構造のデータに対して便利です。
この記事では、再帰の定義、Tree構造の簡単な確認をして、そのあとでTree構造に対し再帰処理を行う例を示しています。
コードはkotlinを使っていますが、なるべくkotlinに触れたことのない方でも読めるように書いているつもりです。逆にkotlinに慣れている方は書き方に違和感(var, valとかforループとか)があるかもしれませんが、ご了承ください。
1. 再帰とは?
こんな感じです(fun は関数定義の接頭語です)。
fun 再帰関数(args){
(何らかの処理)
if(条件){
再帰関数(args)
}
(何らかの処理)
return
}
ここで関数 「再帰関数」 は処理の中で、自分自身を呼び出しています。これが再帰です。
ちなみに、googleで「再帰」と検索すると、「もしかして:再帰」というリンクがでてきて、それを踏むとまた再帰の検索画面が表示されるので、まさに再帰の構造を体験できるようにできています。
上記コードで、ifの分岐を書かないと、メモリがつきるまで処理が終わりません。ですので、再帰関数では、条件満たす場合のみ再帰呼び出しをするといった場合分けが重要です。
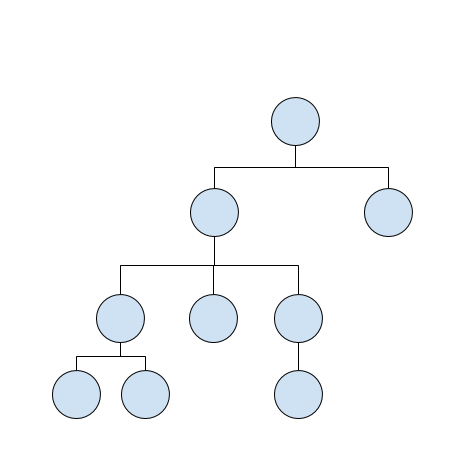
2. Tree構造とは
- 親子構造を持つデータ
- 親から見て子は何個でも存在してOK (0個でもOK)
- 子から見て親は1つだけ
という構造です。トーナメント表みたいなやつ(?)です。上の絵で、各〇のことを、「ノード: node」と呼びます。一番上の〇のことを「ルート: root」と呼びます。ルートは、親が存在しない唯一のノードです。
例えば、パソコンのフォルダとファイルの配置はTree構造をしています。
C:\
├─フォルダ1
│ ├─フォルダ1-1
│ │ ├─ファイル1-1-1.txt
│ │ └─ファイル1-1-2.xls
│ └─フォルダ1-2
│ └─ファイル1-2-1.doc
└─フォルダ2
- C:\ ⇒ ルート
- C:\フォルダ1⇒ C:\ を親に持つノード
- C:\フォルダ1\フォルダ1-1 ⇒ C:\フォルダ1 を親に持つノード
- C:\フォルダ1\フォルダ1-2 ⇒ C:\フォルダ1 を親に持つノード
- C:\フォルダ1\フォルダ1-1\ファイル1-1-1.txt ⇒ C:\フォルダ1\フォルダ1-1 を親に持つノード。子は持たない。
・・・
みたいに、Tree構造を形成しています。
3. Tree構造に対して再帰を使ってみる
Tree構造に対して再帰処理を行ってみます。kotlinで書いています。
いったんコードを全部載せますと、以下のようになります。各々の部分について、そのあとで説明します。
fun main(args : Array<String>) {
// 各ノードの定義
var rootNode = TreeNode("C:")
var folder1Node = TreeNode("フォルダ1")
var folder2Node = TreeNode("フォルダ2")
var folder11Node = TreeNode("フォルダ1-1")
var folder12Node = TreeNode("フォルダ1-2")
var file111Node = TreeNode("ファイル1-1-1.txt")
var file112Node = TreeNode("ファイル1-1-2.xls")
var file121Node = TreeNode("ファイル1-2-1.doc")
// ノード間の親子関係の紐づけ
rootNode.addChild(folder1Node)
rootNode.addChild(folder2Node)
folder1Node.addChild(folder11Node)
folder1Node.addChild(folder12Node)
folder11Node.addChild(file111Node)
folder11Node.addChild(file112Node)
folder12Node.addChild(file121Node)
// パスの取得
println(getFullPath(file112Node))
// すべての子孫の取得
var nodesList: MutableList<TreeNode> = mutableListOf()
getAllDescendants(rootNode, nodesList)
for(i in 0..nodesList.size -1){
println(nodesList[i].data)
}
}
// パスを取得する関数
fun getFullPath(node: TreeNode): String{
if (node.parent == null){
// ルートノードの処理
return node.data
}else{
// ルートじゃないノードの処理
return (getFullPath(node.parent!!) + "\\" + node.data)
}
}
// 引数:base のすべての子孫要素の取得する関数
fun getAllDescendants(base: TreeNode, storingList: MutableList<TreeNode>){
storingList.add(base)
for(i in 0..base.children.size -1){
getAllDescendants(base.children[i], storingList)
}
}
// 各ノードを表すクラス
// parentとchildrenで各ノードが紐づいている
class TreeNode(
var data: String
){
// 親ノード(0または1個のノード)
var parent: TreeNode? = null
// 子ノード(1個以上のノード)
// mutableListOf()はからのリストを作成しています。
var children: MutableList<TreeNode> = mutableListOf()
// 子ノードの追加
fun addChild(child: TreeNode){
child.parent = this
children.add(child)
}
}
3.1. 準備
まず、Tree構造を持つデータのクラスを定義します。(varは変数定義の接頭語です。)
// 各ノードを表すクラス
// parentとchildrenで各ノードが紐づいている
class TreeNode(
var data: String
){
// 親ノード(0または1個のノード)
var parent: TreeNode? = null
// 子ノード(1個以上のノード)
// mutableListOf()はからのリストを作成しています。
var children: MutableList<TreeNode> = mutableListOf()
// 子ノードの追加
fun addChild(child: TreeNode){
child.parent = this
children.add(child)
}
}
ここで、dataは文字列で、例えば「フォルダ1」とか「ファイル1-1-1.txt」とかが設定されます。parentとchildren は同じクラスのインスタンス変数です。ただしchildrenはリストになっています。Tree構造では親が1に対して子が複数存在するからです。
addChildメソッドを呼ぶと、引数で指定したノードが、自分の子供になり、自分が、引数で指定したコードの親になります。
次にメイン関数で、このクラス(ノード)のインスタンスを作成します。
fun main(args : Array<String>) {
// 各ノードの定義
var rootNode = TreeNode("C:")
var folder1Node = TreeNode("フォルダ1")
var folder2Node = TreeNode("フォルダ2")
var folder11Node = TreeNode("フォルダ1-1")
var folder12Node = TreeNode("フォルダ1-2")
var file111Node = TreeNode("ファイル1-1-1.txt")
var file112Node = TreeNode("ファイル1-1-2.xls")
var file121Node = TreeNode("ファイル1-2-1.doc")
各フォルダ、ファイルの名前を設定しています。
そして、各ノードを紐づけます。
// ノード間の親子関係の紐づけ
rootNode.addChild(folder1Node)
rootNode.addChild(folder2Node)
folder1Node.addChild(folder11Node)
folder1Node.addChild(folder12Node)
folder11Node.addChild(file111Node)
folder11Node.addChild(file112Node)
folder12Node.addChild(file121Node)
addChildメソッドを呼ぶことで、ノード間に親子関係を設定しています。
ここまでで、先ほどのフォルダ構造をデータ化できました。↓再掲
C:\
├─フォルダ1
│ ├─フォルダ1-1
│ │ ├─ファイル1-1-1.txt
│ │ └─ファイル1-1-2.xls
│ └─フォルダ1-2
│ └─ファイル1-2-1.doc
└─フォルダ2
3.2. 再帰関数
今回のコードで再帰を使っている部分は、以下の二つです。
// パスを取得する関数
fun getFullPath(node: TreeNode): String{
if (node.parent == null){
// ルートノードの処理
return node.data
}else{
// ルートじゃないノードの処理
return (getFullPath(node.parent!!) + "\\" + node.data)
}
}
// 引数:base のすべての子孫要素の取得する関数
fun getAllDescendants(base: TreeNode, storingList: MutableList<TreeNode>){
storingList.add(base)
for(i in 0..base.children.size -1){
getAllDescendants(base.children[i], storingList)
}
}
getFullPath関数は、引数のノードが親を持っていたら、さらにその親をたどっていって、文字列連結をする関数です。この関数で、ルートからのフルパスを取得することができます。
// パスの取得
println(getFullPath(file112Node))
↓
C:\フォルダ1\フォルダ1-1\ファイル1-1-2.xls
また、getAllDescendants関数では、子供がいれば、さらにその子供をたどっていくことで、すべての子孫要素を取得(してstoringListに代入)する関数となっています。
// すべての子孫の取得
var nodesList: MutableList<TreeNode> = mutableListOf()
getAllDescendants(rootNode, nodesList)
for(i in 0..nodesList.size -1){
println(nodesList[i].data)
}
↓
C:
フォルダ1
フォルダ1-1
ファイル1-1-1.txt
ファイル1-1-2.xls
フォルダ1-2
ファイル1-2-1.doc
フォルダ2
重要なのは、getFullPathではif文を利用して、getAllDescendantsではforループを利用して、再帰の終了が条件づけられていることです。(childrenのサイズが0の時は、forブロックの中に入らないので、それ以上再帰されません。)
3.3. 考察
Tree構造に対し再帰関数を使うことによって、祖先や子孫を取得する例を見てきました。
Tree構造は階層(ルートからの距離)の数が固定されていないので、何階層たどればルートや一番下のノードまでたどり着けるかがわかりません。その状況でも、再帰関数を使うことで過不足なく処理を行うことができると思います。
今回の例では、文字列のみ持つデータを使いましたが、実際にはファイルかフォルダかの判定、ファイルサイズ、ファイルの種類(拡張子)などをデータに持たせれば実用性が高まると思います。また、今回は子の追加のみ実装していますが、実際には親子関係の削除の機能が必要になります。それと、データ構造を壊さないように、parent, childrenはprivateとか最低でもprotectedにしなければいけないと思います。
Tree構造のデータはほかにもDOMやjsonなどあるので、それらに対しても有効であると思います。
以上