Problem
この問題では、n段の階段を1段または2段ずつ上る場合の独自の方法の数を求めることが目的です。つまり、いくつの異なる組み合わせで階段の上まで到達できるかを計算することが求められています。
You are climbing a staircase. It takes n steps to reach the top. Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
InputとOutputの例は次になります。
Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
Key Idea
この問題はクラシックな問題で、再帰、Dynamic Programming(動的計画法)、またはそのコンビネーションによって解くことができます。
具体例を使って考えると、この問題の構造がフィボナッチ数列に似ていることがわかります。
- n = 1の場合、1通りの方法しかありません(1段登る)。
- n = 2の場合、2通りの方法があります(1段ずつ登る、または2段一度に登る)。
- n = 3の場合、n = 2の場合の方法に1段登る方法を追加したものと、n = 1の場合の方法に2段登る方法を追加したもので、計3通りの方法があります。
- n = 4の場合、n = 3の場合の方法に1段登る方法を追加したものと、n = 2の場合の方法に2段登る方法を追加したもので、計5通りの方法があります。
これを一般化すると、n段登る方法の数は、n-1段登る方法の数とn-2段登る方法の数の和になります。
Approach #1 再帰
「n段登る方法の数は、n-1段登る方法の数とn-2段登る方法の数の和」ということから再帰を使うことが考えられます。ただし、再帰を使った解法は、O(2^n)であるため、Leetcodeでは、Time Limit Exceededになってしまいます。
class Solution:
def climbStairs(self, n: int) -> int:
if n == 1:
return 1
elif n == 2:
return 2
return self.climbStairs(n-1) + self.climbStairs(n-2)
Approach #2 Dynamic Programming (A)
Dynamic Programmingでは、計算結果を途中で保存しておき、再利用することで効率的に問題を解くことができます。
具体的には、Decision treeのようにN段目までの到達方法をパターン分岐させると、下記のようになります。
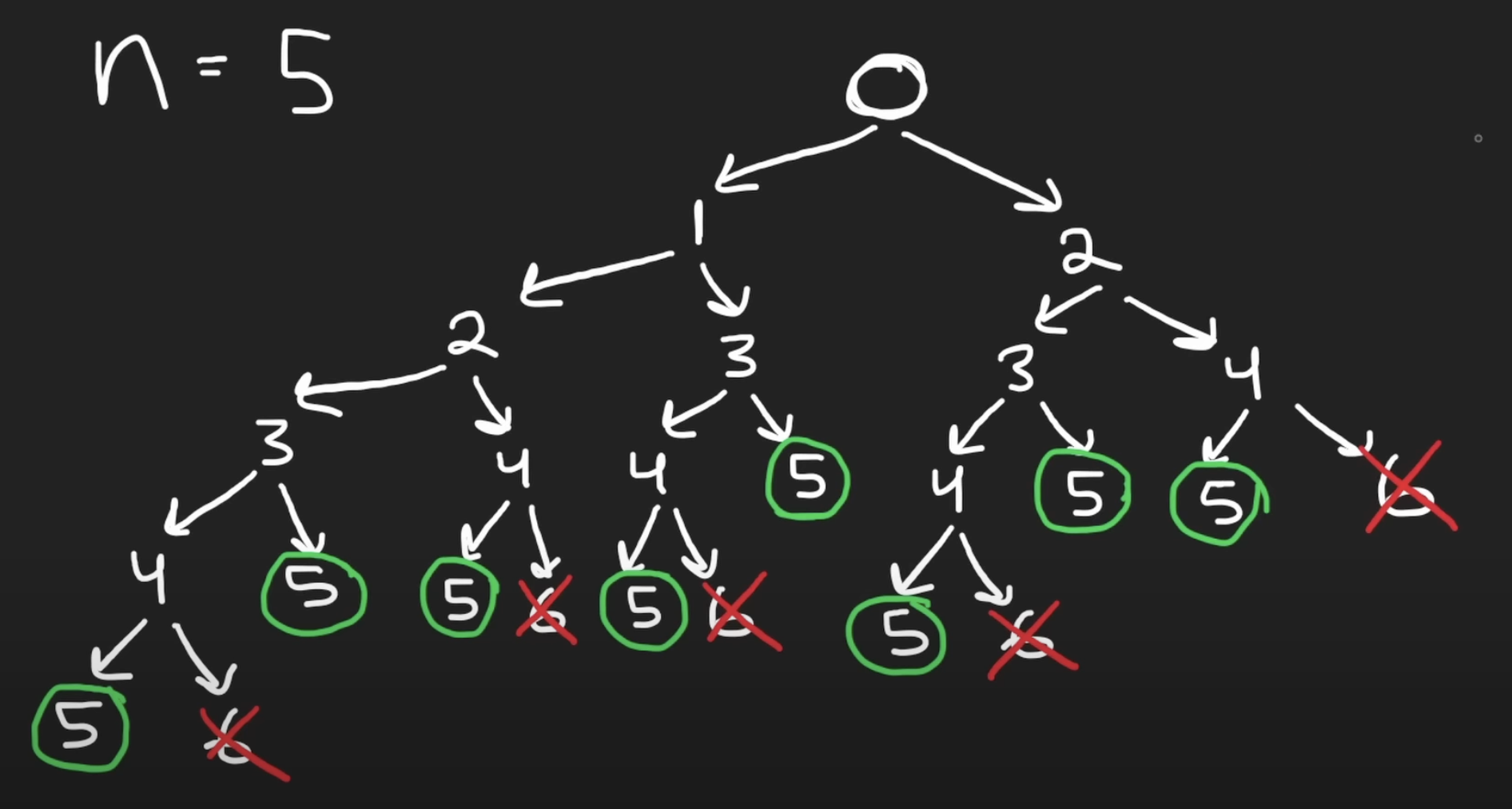
N段目までの到達方法をメモしておく場合、ほとんど枝刈りをすることができ、O(n)の計算量になります。
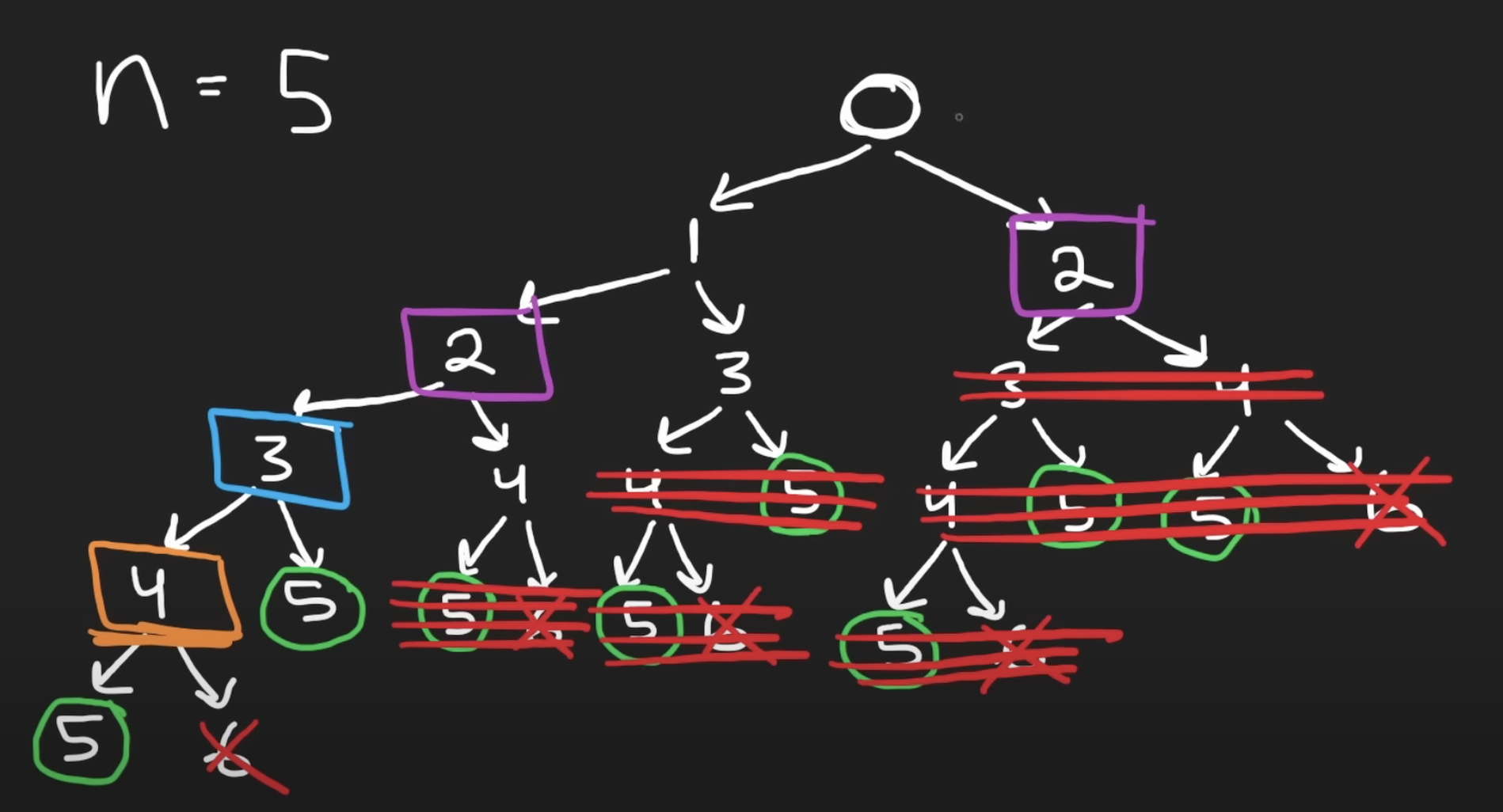
下記がサンプルコードになります。dpという配列についてですが、0番目は初期化状態のまま特に利用せず、1番目からn番目までを使っています。そのため、要素数はn+1個含むように配列を初期化しています。
class Solution:
def climbStairs(self, n: int) -> int:
if n == 1:
return 1
elif n == 2:
return 2
dp = [None] * (n + 1)
dp[1] = 1
dp[2] = 2
for i in range(3, n+1):
dp[i] = dp[i-1] + dp[i-2]
print(i)
return dp[n]
Approach 3: Dynamic Programming (B)
Approach 2の方法は、配列を使うことでO(n)の空間計算量を必要としていました。しかし、n段登る方法の数は、n-1段登る方法の数とn-2段登る方法の数の和になるため、それぞれを、prev1とprev2という変数に保存しておけば、メモリを効率化させることができます。
class Solution:
def climbStairs(self, n: int) -> int:
if n == 1:
return 1
elif n == 2:
return 2
prev1 = 1 # n-1段登る方法の数
prev2 = 2 # n-2段登る方法の数
for i in range(3, n+1):
current = prev1 + prev2
prev1 = prev2
prev2 = current
return current
Complexity Analysis
計算量は下記の様になります。
| Approach | Time complexity | Space complexity |
|---|---|---|
| 1. Recursion | O(2^n) | O(n) |
| 2. DP(A) | O(n) | O(n) |
| 3. DP(B) | O(n) | O(1) |
Reference