Leetcode 104. Maximum Depth of Binary Tree

Problem

与えられた二分木の最大深度（根から最も遠い葉ノードまでのノード数）を求めるというものです。

Given the root of a binary tree, return its maximum depth.

InputとOutputの例は次になります。

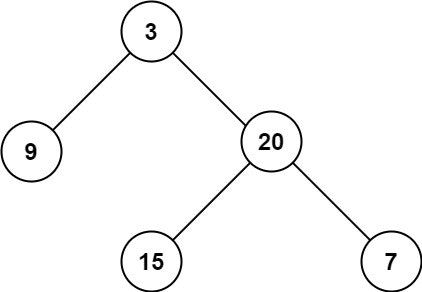
Input: root = [3,9,20,null,null,15,7]
Output: 3

X

Key Idea

深さ優先探索 (DFS) または幅優先探索 (BFS) を用いて解くことができます。

Approach #1 Depth-First Search (DFS) using Recursion

DFS の特性を利用した解法で、各パスを深く探索し、それぞれの深度を比較します。再帰を利用して実装することができます。

class Solution:
    def maxDepth(self, root):

        if root is None: 
            return 0 
        else: 
            left_height = self.maxDepth(root.left) 
            right_height = self.maxDepth(root.right) 
            return max(left_height, right_height) + 1 

Approach #2 Depth-First Search (DFS) using Stack

深さ優先探索 (DFS) は再帰を使わずにスタックを使用することでも実装することができます。Pythonではスタックは、collections.dequeを利用することもできますが、ここではシンプルにlistを利用しています。

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root is None:
            return 0
        
        stack = [[root, 1]]
        depth = 0

        while stack:
            node, current_depth = stack.pop()

            if node:
                depth = max(depth, current_depth)
                stack.append([node.left, current_depth + 1])
                stack.append([node.right, current_depth + 1])

           
        return depth

Approach #3 Breadth-First Search (BFS)

幅優先探索 (BFS) の場合、各レベル（深度）を順に探索していき、最後に探索したレベルが最大深度となります。キューを用いて各レベルのノードを順に探索し、新たにノードが見つからなくなった時点での深度が最大深度です。

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root is None:
            return 0
        
        queue = collections.deque([(root, 1)])


        while queue:
            node, depth = queue.popleft()
        
            if node.left:
                queue.append((node.left, depth+1))
            
            if node.right:
                queue.append((node.right, depth+1))
           
        return depth

Complexity

Time complexityは、上記解法の全ての場合で、O(n)となります。ここで、nはノード数です。全てのノードを一度だけ訪問するためです。

Space complexityは、どのパターンでも最悪計算量はO(n)ですが、それぞれ得意・不得意な木の形があります。

Approach #1, #2 :Depth-First Search (DFS)

• 最も都合が良い場合：O(log n)。完全に平衡している二分木の場合、最大のスタックの深さが考慮されるため、平衡した木ではスタックの深さが最小化され、その結果としてO(log n)となります。
• 最も都合が悪い場合：O(n)。木がほとんど一直線（リストのよう）になっている場合、最大の再帰スタックの深さが考慮されるため、非常に偏った木では再帰スタックの深さが最大となり、その結果としてO(n)となります。
• 再帰を使ってもスタックを使っても同じ計算量になりますが、違いとしてはスタックオーバーフローの対処になります。再帰DFSはシステムスタックを使用し、スタックの最大サイズは実行環境によります。したがって、深いツリーを探索するとスタックオーバーフローが起こる可能性があります。スタックDFSは手動でスタックを作成して管理するため、再帰DFSに比べてスタックオーバーフローのリスクを減らすことができます。ただし、スタックの管理が必要なため、コードが少し複雑になる可能性があります。

Approach #3 : Breadth-First Search (BFS)

• 最も都合が良い場合：O(log n)。二分木がほとんど一直線（リストのよう）になっている場合。各レベルに1つのノードしかないため、キューには常に1つのノードしか存在しません。
• 最も都合が悪い場合：O(n)。平衡二分木の場合、各レベルでノードの数が倍になるため、最深レベルではn/2のノードが存在し、これがBFSのキューに全て格納される場合があるため、スペース計算量はO(n)となります。

Reference