*この記事は統計学や機械学習を専門としていない学生が書いた主観的なまとめ記事です。間違いが含まれている可能性があります。
統計学・機械学習を学んでいると、たくさんの手法や考えが出てきてよくわからなくなります。
特に自分が何かに取り組んでいるときには、今やっている手法が全体から見てどういうものなのか、より良い手法が無いのかが気になってしまいます。
まるで地図を持たず森の中を彷徨っているような感覚です。
そこで、統計学・機械学習で使われる概念や手法を自分なりにまとめて頭を整理したいと思います。
以下のような図になりました。
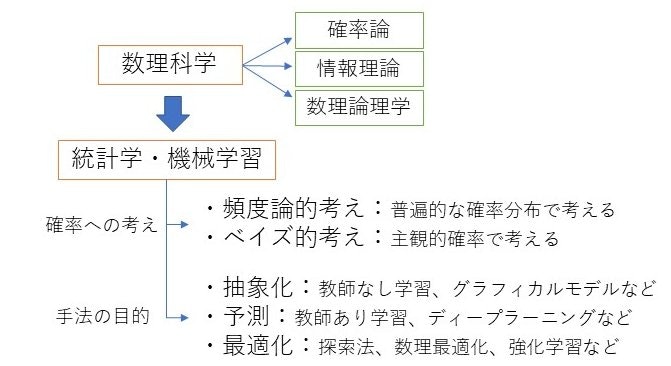
以下にそれぞれを説明します。
数理科学
統計学・機械学習のベースとなる学問です。
主に解析学、代数学、幾何学からなります。
微分積分学と線形代数学が基本になってるのは言うまでもないと思います。
その他に個人的に関わりが深いと思う分野を3つ挙げます。
確率論
大数の法則(中心極限定理)の証明に必要になります。
時系列変化する確率を扱うのが確率過程です。
確率微分方程式、測度論、ルベーグ積分などが関わります。
情報理論
エントロピーや情報量などを扱います。通信の効率化などの応用もあります。
数理論理学
記号論理学とも言われ、哲学の分野でもあります。
あらゆる数学の基礎になります。
古くには記号論理的AIなどへ応用されました。
知識工学の概念でもあるオントロジーも関係します。
統計学・機械学習
データを取り扱うという意味では統計学と機械学習はとても似ていますし、重なっています。
工学的にはパターン認識やAIのソフト部分を担うものです。
統計学・機械学習は、A:目的、B:確率の考え方の2つの要素があると思います。
AとBの組み合わせで、統計学や機械学習の手法が表のように6つに分類できると考えます。
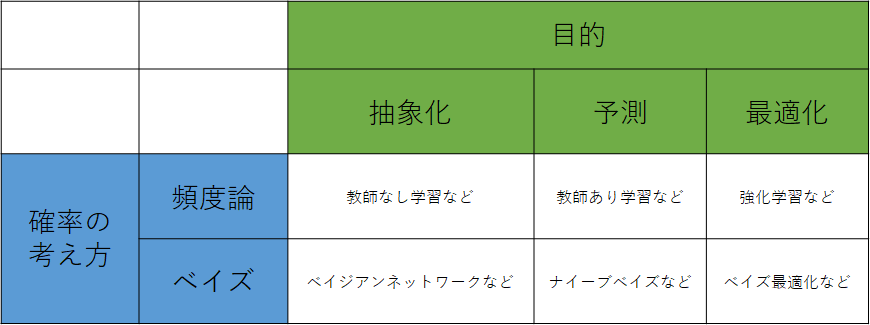
実際にベイズを使った手法として、ナイーブベイズ、ベイジアンネットワーク、ベイズ最適化だけでなく、ベイズ的仮説検定、ベイズ線形回帰、ベイズクラスタリング、ベイジアンニューラルネットワークといった手法もあります。
A:目的<抽象化or予測or最適化>
様々な手法がありますが、目的別で分けると分かりやすいと思います。
目的は
1抽象化 2予測 3最適化
の3つに分けました。
目的1:抽象化
そのデータからわかる傾向や性質と取り出すということです。
何らかの事実を主張したり、可視化したりします。
以下具体的な手法です。
検定・推定・相関
統計の基本ですが、これで母集団の性質を推測します。
結果が真偽や数値だけになるため、抽象化の度合いが強いです。
検定では帰無仮説の棄却によって結論を導きます。
回帰分析
回帰分析は、変数同士の関係を数式に表すものです。
一番基本的なのは単回帰や重回帰、多項式回帰などの線形回帰だと思います。
線形回帰は最小二乗法で計算をするため、基本的には誤差が正規分布であることが前提にあります。
ちなみにこの前提は、t検定、F検定、分散分析、共分散分析にもあり、これらは全て本質的には同じものとしてまとめて一般線形モデルと言われます。
指数型分布族の誤差にも適応できるようにしたのが、一般化線形モデル(GLM)です。
例えば、GLMの1つのロジスティック回帰によって、2値分類問題を扱うことが出来ます(確率が出力される)。
さらに拡張した一般化線形混合モデル(GLMM)では変量効果も扱います。
また、GLMを非線形関数の和に拡張した一般化加法モデル(GAM)もあります。
以上に加えて、時系列データでは自分に対する回帰分析(自己回帰)を考えることも出来ます。AR、ARMA、ARIMAなどです。古典制御理論も関係します。
判別分析
判別分析は、分類問題において異なるクラスに分かれているデータを判別するための判別関数を求めるものです。
線形判別分析(LDA)や二次判別分析(QDA)、正準判別分析(CDA)などがあります。
正規分布モデルであることなどの前提があります。
クラス間の変動とクラス内の変動の比を最大化します。
大津の2値化である判別分析法も関係しているのではないかと思います。
状態空間モデル
状態空間モデルは主に時系列データに対して行います。
状態と観測の2つの段階に分けて、状態そのものは直接見ることが出来ない潜在変数と考えます。
(状態がそのまま観測される場合は、時系列の回帰分析と同じになります。)
状態の遷移を表す状態方程式と、状態から観測値を出す観測方程式の2つを考えます。
現代制御理論の基礎な考えでもあり、カルマンフィルタやパーティクルフィルタなどがあります。
また、シミュレーションの側面も強く、データ同化に応用されます。
状態空間モデルの潜在変数が離散の場合が、隠れマルコフモデルになります。
教師なし学習(クラスタリングや次元削減)
似たものを同じクラスとして分類したり、データを2次元にして平面にマッピングしたりします。
クラスタリングではk-means法、混合ガウスモデル、階層的クラスタリングなどがあります。
次元削減ではPCA(主成分分析)、ICA(独立成分分析)、LSA(潜在意味解析)、LDA(潜在的ディリクレ配分法)、NMF(非負値行列因子分解)などがあります。
PCAはSVD(特異値分解)とほとんど等価な処理をしていますし、LSAはtruncated SVDです。
他に多様体学習のIsomap、LLE、tSNE、UMAPも次元削減です。
またSOM(自己組織化マップ)も低次元空間への写像のため次元削減です。
グラフィカルモデル
変数の関係をグラフに表します。有向グラフもあれば無向グラフもあります。
無向グラフでは偏相関係数グラフなどです。
因果推論
グラフィカルモデルに似ていますが、関係の中でも因果関係に重点を置きます。
因子分析、共分散構造方程式(SEM)などがあります。
因子分析は主成分分析と似てますが、共通因子の数を事前に指定する必要があります。
反事実、バックドア基準などの概念があります。
生成モデル
Deep LearningにおけるGANやVAEなどです。データの性質を把握して、同じようなデータを作れるようにします。
また制限ボルツマンマシンもニューラルネットワークを用いた生成モデルです。
目的2:予測
今までのデータを学習させることで、同じようなデータではどうなるかを予測します。
自動診断などのAIで応用されます。
以下具体的な手法です。
回帰分析・判別分析・状態空間モデル
抽象化にもありました。データの関係性をモデルで表すので、新しいデータを当てはめれば予測に使うことができるということです。
教師あり学習(特徴量学習器)
本来の教師あり学習の意味は広いですが、ここではテーブル形式の特徴量データ入力として学習するものを考えます。
決定木やk-NN法、SVM(サポートベクトルマシン)、RVM(関連ベクトルマシン)、距離学習などがあります。
決定木は条件分岐を繰り返して分割していく手法です。ID3、C4.5、CARTなどのアルゴリズムがあります。汎用的な手法で結果の可読性も高いですが、過学習しやすくて単体での精度は良くないです。
k-NN法も汎用的ですが、データ数が多く必要になります。特に、入力次元が大きくなると必要なデータが膨大になります。(次元の呪い)
そこで、SVMが使われます。SVMはマージン最大化によって境界になる超平面を求めます。線形分離ができない場合には、カーネル法によって高次元の特徴空間の写像によって線形分離を可能にさせる方法があります。RVMはSVMと似ていますが、結果を確率として出力をすることが出来ます。
距離学習はデータ間の距離(類似度、関係性)が分類に最適になるようにデータ空間を変換するという手法です。マハラノビス距離やKISSMEなどがあります。単一ラベルの時は異常値検知など教師なし学習的な使用もできます。
ここからは予測に特化していくので、予測根拠の説明が難しくなっていきます。
ニューラルネットワーク
単純パーセプトロン自体はロジスティック回帰と等価ですが、多層にすることで複雑なものにも対応できるようになりました。
Deep Learningによる識別器では、画像や音声、テキストデータなどの複雑なデータも扱えます。
Deep Learningの発展的な構造としては、畳み込みニューラルネットワーク(CNN)や再帰的ニューラルネットワーク(RNN、GRUやLSTMなども)、Attentionなどがあります。
また通常のネットワークは予測値を出力させますが、深層距離学習では特徴量空間を出力させます。
学習手法である誤差逆伝播法では、ヒューリスティックな最適化手法である勾配法(特に確率的勾配降下法)を用いています。
他にも神経科学の観点から新しい学習方法が提案されています。スパイキングニューラルネットワーク(SNN)のSTDPやEGHRなど。
また、リザーバーコンピューティングはRNNの特殊型です。
他にもニューラルネットワークの発展形には、ベクトルを入出力するCapsNetや、RNNなどの層を連続化して常微分方程式として扱うODENetなどもあります。
アンサンブル学習
これ自体が新しい予測手法ではなく、予測の結果を組み合わせて予測精度の向上を図るという手法です。
例えば、リサンプリングでデータを変えたり、または予測手法を変えたりしたもののそれぞれの結果を組み合わせる(回帰問題では平均をとる、分類問題では多数決をとる)ことも単純なアンサンブル学習になります。
他に有名なものでは、バギング(ブートストラップ・アグリゲーティング)、ブースティング、スタッキングがあります。
バギングやブースティングでは、1種類の手法にデータを変えて学習させるのに対して、スタッキングでは、同じデータに対して手法を変えて学習させるようです。
バギングやブースティングで組み合わせ予測手法1つ1つのことを弱学習器と言い、これには、基本的に決定木が用いられます。(これは決定木が高速で汎用性が高い手法であるからだと思います。)
例えば、ランダムフォレストは決定木をバギングしたものです。バギングは学習データを復元抽出したものを組み合わせるだけであるため、並列で行うことが出来る利点があります。また、バギングはバリアンスを減らして過学習を抑制します。
一方で、ブースティングは逐次的に弱学習器を学習させるため直列で行われます。ブースティングはバイアスを減らして学習不足を解消します。
適応型ブースティング(AdaBoost)は結果を踏まえてデータの重みを更新して(間違えたデータの重みを大きくする)次の学習を行うもので、最終的には各学習器の結果の重み付き多数決を出力とします。
勾配ブースティングは結果で出された予測と正解値との誤差(一般的には損失関数の負の勾配)を正解値として学習していくもので、最終的には各学習器の結果の足し合わせが出力となります。勾配ブースティング決定木はかなり有効な手法で、XGBoost, LightGBMはとても有名です。
メカニズム的には適応型ブースティングが分類木、勾配ブースティングが回帰木に用いるような印象がありますが、実際はどちらも拡張して両方に適応できるようです。
スタッキングは2段階に積み上げて行う手法で、1段階目では、ニューラルネットワークなど様々な手法が使用されます。1段階目で得られた結果を新しい特徴量として学習データに組み込みます。この際に正解データが使われないようにクロスバリデーションを行います(そうしないと学習データで正解をカンニングした特徴量が生成されてしまう)。次に2段階目では、1段階目で得られた特徴量のテーブルデータ(これに元からある特徴量も加えることもある)を学習して、出力します。このスタッキングをさらに何段回も繰り返すことも出来ます。
またスタッキングでは特徴量を上手くとることが大切であるため、必ずしも予測手法を組み合わせる必要はなく、教師なし学習を用いることも考えられます。
目的3:最適化
ある状況における最適な変数の値や行動を求めるものです。ゲームなどの勝負系のAIなどで応用されます。
例えば、ある関数が最小値をとる変数を探すことを考えます。最小値は、簡単な関数では(微分)=0することで求められますが、実際には関数が複雑や不明だったり、変数領域が制限されているので単純にはいきません。そのため、最適化手法が必要になります。
また、最適化問題は、当たり前ですが全てのパターンを試して比べれば必ず最適解を求めることが出来ます(総当たり法)。しかし、実際のところ全てを試すことは不可能であるため、様々な手法が提案されているのです。
以下具体的な手法です。
探索法
分枝限定法やA*探索、ダイクストラ法などです。
迷路やグラフでの最短経路を求めることが出来ます。
実験計画法
効率の良い実験を設計するものです。
例えば許容できる誤差や信頼度から最適なサンプルサイズを求めることが出来ます。
また、フィッシャーの3原則(反復、無作為、局所管理)という概念や
直交計画法、コンジョイント分析、検出力分析などがあります。
品質工学などに応用されます。
数理最適化
線形計画法や非線形計画法などがあり、KKT条件や双対定理などの概念が提案されています。
難解は問題としては、組み合わせ最適化(離散最適化)問題(例えば巡回セールスマン問題やナップサック問題など)があります。このような難解な問題でも、動的計画法によって解くことが可能です。
動的計画法は、問題を部分問題に分割して記録しながら移動して解いていくという探索法的な解法です。
そのため、動的計画法は問題によっては非常に時間がかかります。
ここで、必ずしも最適解が求められなくてよいという考えが出てきます。
時間がかかる厳密解法ではなく、短時間で計算できる近似解法も需要があるということです。
そこでヒューリスティクス(発見的方法)が開発されて、汎用的なものはメタヒューリスティクスと呼ばれます。
メタヒューリスティクスには、遺伝的アルゴリズムや焼きなまし法、群知能を用いた方法などがあります。
ただし、全ての問題で性能の良い万能な近似解法は存在しないとされます。(ノーフリーランチ定理)
強化学習
強化学習はマルコフ決定過程と深く関係する最適化手法です。
強化学習も厳密解が求まるとは限らない近似解法ですが、複雑な問題での精度が高いと思います。
前述の動的計画法は厳密解を求めることが出来ますが、未知の環境では適用できません。
強化学習は近似解法のため、環境に対する完全な理解が無くても適用することができます。
報酬を設定し、何回も行動して試行錯誤して最適な行動を探すアルゴリズムです。
環境と相互作用しながら、累積報酬を最大化する行動を学習します。
Deep Learningを取り入れたDQNなど深層強化学習もあります。
B:確率の考え方<頻度論orベイズ>
確率の考え方は頻度論とベイズの2つがあります。
2つは主義として対立的に語られることもありますが、実際は状況に応じて使い分けられていると感じます。
基本的なイメージは、単純なモデルは頻度論的に、複雑なモデルはベイズ的に考えることになるかと思います。
頻度論では未知のものを定数として求めます「推定(estimation)」。そのため、頻度論では結果が解釈しやすいですが、モデル構造やハイパーパラメータを決定的なものとして扱い、複雑なモデルに対応しにくいです。
一方で、ベイズでは未知のものを確率分布で求めます「推論(inference)」。ベイズは確率変数を増やすことで複雑なモデルでも柔軟に対応できますが、計算が複雑です。
頻度論
頻度論では、普遍的な確率分布を考えます。確率分布のパラメータは一定であると仮定され、これを求めます。
確率分布の形状は変化しません。最尤法でパラメータを推定します。
また、そもそも確率分布を仮定しないノンパラメトリックな手法もあります。例としては、ノンパラメトリック検定、ノンパラメトリック回帰、カーネル密度推定、k-NN法などです。ノンパラメトリックな手法はあらゆる状況に適応できますが、その分多くのデータ数が必要になります。(頑強性と効率性のトレードオフ)
ベイズ
ベイズでは主観確率で考え、確率分布そのものを求めます。
まず事前分布が設定され、そこにデータの尤度が掛け算されて事後分布が作られます。
データが増えたら、確率分布が形状も含めて変化していきます。
事前分布には自分の知識を入れることが出来ます。
パラメータが確率変数として更新されていきます。
階層化することで、ハイパーパラメータも確率変数として扱えます。
柔軟な考えができますが、計算が複雑になります。そこで、ラプラス近似や変分ベイズによる近似、MCMC法によるシミュレーションで計算が行われます。
ベイズの中でもノンパラメトリックベイズでは、無限混合モデルによってモデル構造も確率変数として自動決定できるので、より柔軟なモデルが作れるようです。
正則化(スパースモデリング)について
よく過学習を防ぐのに役立つ正則化ですが、これはパラメータの事前分布を規定しているとも考えることが出来て、そういう意味でベイズ的な考えになります。
またモデル選択に使われる情報量基準もベイズ的な考えを取り入れています。ただし有名な赤池情報量基準(AIC)は期待対数尤度の推定量で、ベイズではありません。
最後に
筆者自身がまだ勉強中の身ですが、このように色んな手法を1つにまとめてみると勉強のモチベーションに繋がります。
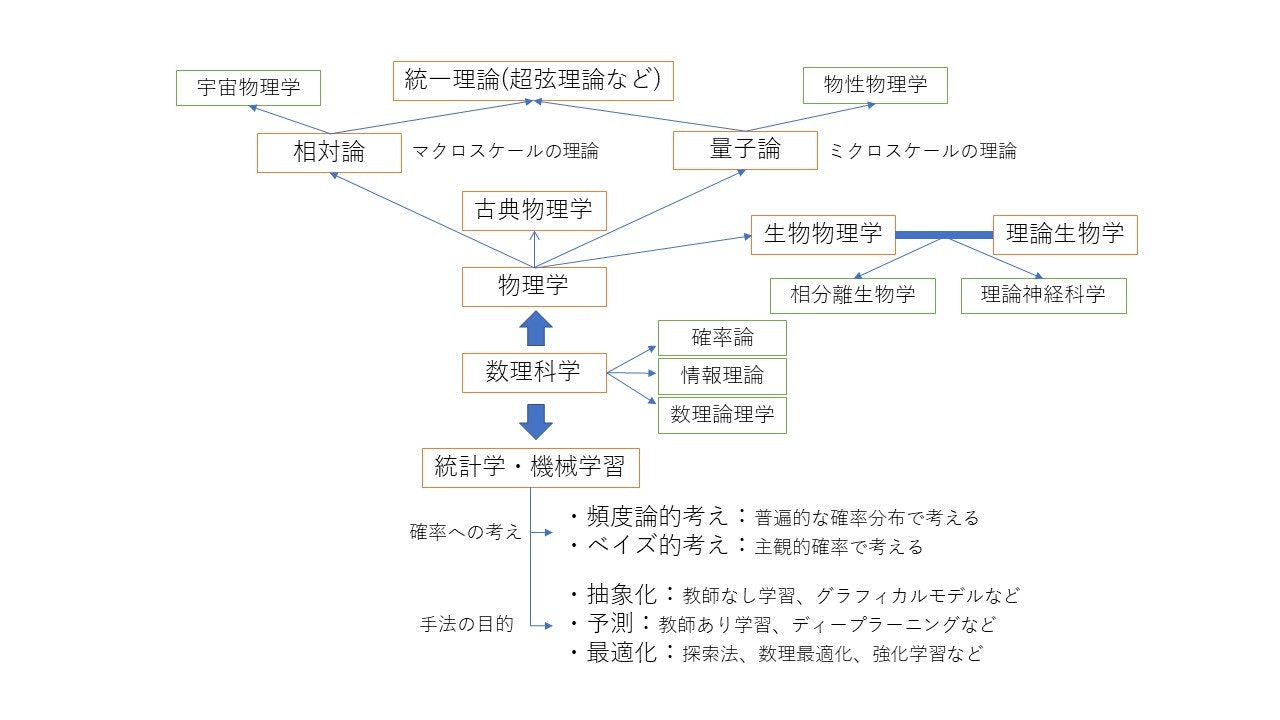
余談ですが、本当は図に物理学も加えて以下のようにざっくりまとめてました。
生物学が入っているのは自分の興味からです。これからも勉強を継続していきたいと思います。
以下は勉強の参考になると思った書籍です。
①統計学入門(東京大学出版会)
②データ解析のための統計モデリング入門
③初めてのパターン認識
④分かりやすいパターン認識
⑤続・分かりやすいパターン認識
⑥パターン認識と機械学習(上・下)
⑦統計的学習の基礎
⑧深層学習(Goodfellow著)
⑨これなら分かる最適化数学
⑩強化学習 (機械学習プロフェッショナルシリーズ)