ヒープをポインタで構築した C++

概要・背景

この記事ではヒープの説明等はしないのでヒープについて知りたい人は他の記事をあたって下さい。
ヒープの構築は配列を用いて実装されていることがほとんどです。
そこで本記事ではポインタを用いてヒープを構築してみたいと思います。

仕様

以下のようなクラスを用意します。
クラスは根とヒープの大きさ(要素が何個入っているか)の情報のみを持ちます。
またそれぞれのノードの実態としてNodeという構造体を使用します。

myHeap.h

#ifndef _MYHEAP_H_
#define _MYHEAP_H_

class MyHeap {
   private:
    struct Node {
        int value;
        Node *left, *right;
        Node() : left(nullptr), right(nullptr) {}
        Node(int x) : value(x), left(nullptr), right(nullptr) {
        }
        Node *
        operator->() {
            return this;  // pointer
        }
    };
    // 根
    Node *root;
    int size;

   public:
    // constructor
    MyHeap();
    // destructor
    ~MyHeap();
    // function
    void push(int);
    int top();
    void pop();
    void display();
};

#endif  //_MYHEAP_H_

push ヒープへの追加

配列を用いたヒープでは挿入が、配列の末尾に新しい要素を追加すればいいのでO(1)で実現できます。
ポインタを使っている場合は末尾に挿入することを考えると、末尾まで根から辿って行かなければならず、処理にlog2(n)かかってしまいます。
そこで下で説明するような性質を利用し、「挿入場所の方向に進みつつ、ノードを交換するべき場所で交換する」という方針をとります。

性質

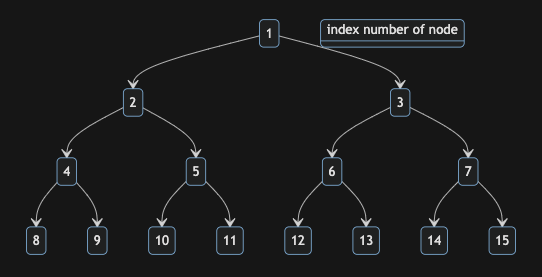
上図のように根から葉に向かって番号を振っていきます。
そして下図のように振られた番号を2進数(bit表示)で表します。

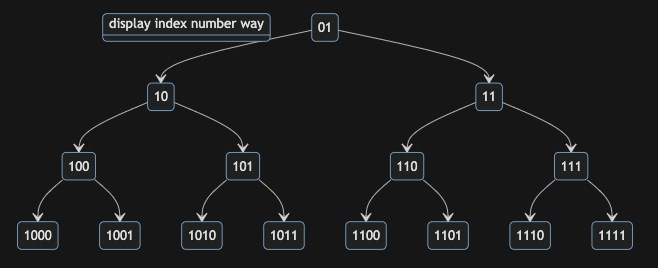
以下のような操作で根から各ノードへ進むことができます。

ノードのbit表示における、左から2番目の文字から最後（一番右）の文字にむかって、
0だったら左のノードへ進む
1だったら右のノードへ進む

例として、木の根（番号1）から番号5が振られたノードに進むことを考えます。
番号5のビット表示は101です。 // 現在地は番号1
左から2番目の文字は0なので左に進む // 現在地は番号2
左から3番目の文字は1なので右に進む // 現在地は番号5 （到達）

以上のような性質を利用して道を進みます。
また以下のコードにおけるgetDepth関数は、番号をビット表示した時の長さを取得しています。getDepth(5)は5のbit表示が101なので3を返します。

myHeap.cpp

int getDepth(int num) {
    int cnt = 0;
    while (num >>= 1) {
        cnt++;
    }
    return cnt;
}
void MyHeap::push(int val) {
    size += 1;
    Node appendNode = Node(val);
    if (size == 1) {
        *root = appendNode;
        return;
    }
    // rootと交換判定
    if (root->value > (appendNode->value)) {
        appendNode->left = root->left;
        appendNode->right = root->right;
        Node temp = *root;
        *root = appendNode;
        appendNode = temp;
        appendNode->left = nullptr;
        appendNode->right = nullptr;
    }
    // 行くべき方向の深さ
    int depth = getDepth(size);
    // 今どこのノードにいるか
    // ポインタのポインタ渡し node変更するとrootも変わる
    Node *node = root;
    // cout << "size: " << size << " size_bit: " << bitset<8>(size) << endl;
    while (depth--) {
        int way = (size >> depth) & 1;  // depthビット目のビット値を取得(0or1)
        // way==1 右へ way==0 左へ
        // 参照渡し
        Node *&nextNode = way ? node->right : node->left;
        if (nextNode == nullptr) {
            nextNode = new Node();
            *nextNode = appendNode;
            break;
        }
        // nextNodeと交換すべきか判定
        if (nextNode->value <= appendNode->value) {
            // 交換しなくていい
            //nodeを更新して処理続行
            node = nextNode;
        } else {
            // 交換
            Node temp = *nextNode;
            *nextNode = appendNode;
            nextNode->left = temp->left;
            nextNode->right = temp->right;
            appendNode = temp;
            appendNode->left = nullptr;
            appendNode->right = nullptr;
            node = nextNode;
        }
    }
    return;
}

top 根の値を返す

myHeap.cpp

int MyHeap::top() {
    if (root == nullptr) {
        cout << "this tree is empty" << endl;
        return 0;
    }
    return root->value;
}

pop 根を削除してヒープの再構築

配列を用いたヒープでは根を削除した後、末尾を根に移動してヒープを再構築します。
ポインタを用いたヒープでも同じアイディアを採用しました。
しかし、末尾を探索する必要があるので、配列時に比べ余分にlog2(n)回時間要します。

myHeap.cpp

void MyHeap::pop() {
    // 行くべき方向の深さ
    int depth = getDepth(size);
    Node *node = root;
    while (depth--) {
        int way = (size >> depth) & 1;
        Node *&nextNode = way ? node->right : node->left;
        if (nextNode->left == nullptr) {
            // 末端とrootを入れ替える
            root->value = nextNode->value;
            way ? node->right = nullptr : node->left = nullptr;
            delete nextNode;
            break;
        }
        node = nextNode;
    }
    // Heap再構築
    queue<Node *> que;
    que.push(root);
    while (!que.empty()) {
        Node *node = que.front();
        que.pop();
        if (node == nullptr) break;
        // left right 小さい方と交換 or
        if (node->left && node->right) {
            if (node->left->value < node->right->value) {
                // left smaller
                if (node->left->value < node->value) {
                    // switch
                    int temp = node->value;
                    node->value = node->left->value;
                    node->left->value = temp;
                }
                que.push(node->left);
            } else {
                // right smaller
                if (node->right->value < node->value) {
                    // switch
                    int temp = node->value;
                    node->value = node->right->value;
                    node->right->value = temp;
                }
                que.push(node->right);
            }
        } else if (node->left == nullptr && node->right == nullptr) {
            break;
        } else if (node->left) {
            if (node->left->value < node->value) {
                // switch
                int temp = node->value;
                node->value = node->left->value;
                node->left->value = temp;
            }
            que.push(node->left);
        } else {
            if (node->right->value < node->value) {
                // switch
                int temp = node->value;
                node->value = node->right->value;
                node->right->value = temp;
            }
            que.push(node->right);
        }
    }
    size -= 1;
    if (size == 0) {
        root = nullptr;
    }
    return;
}

myHeap.h

myHeap.h

#ifndef _MYHEAP_H_
#define _MYHEAP_H_

class MyHeap {
   private:
    struct Node {
        int value;
        Node *left, *right;
        Node() : left(nullptr), right(nullptr) {}
        Node(int x) : value(x), left(nullptr), right(nullptr) {
        }
        Node *
        operator->() {
            return this;  // pointer
        }
    };
    // 根
    Node *root;
    int size;

   public:
    // constructor
    MyHeap();
    // destructor
    ~MyHeap();
    // function
    void push(int);
    int top();
    void pop();
    void display();
};

#endif  //_MYHEAP_H_

myHeap.cpp

myHeap.cpp

#include "myHeap.h"

#include <bitset>
#include <iostream>
#include <queue>

using namespace std;
MyHeap::MyHeap() {
    root = new Node();
    size = 0;
    // cout << "construct my heap" << endl;
}
MyHeap::~MyHeap() {
    delete root;
    size = 0;
    // cout << "destruct my heap" << endl;
}

int getDepth(int num) {
    int cnt = 0;
    while (num >>= 1) {
        cnt++;
    }
    return cnt;
}
void MyHeap::push(int val) {
    size += 1;
    Node appendNode = Node(val);
    if (size == 1) {
        *root = appendNode;
        return;
    }
    // rootと交換判定
    if (root->value > (appendNode->value)) {
        appendNode->left = root->left;
        appendNode->right = root->right;
        Node temp = *root;
        *root = appendNode;
        appendNode = temp;
        appendNode->left = nullptr;
        appendNode->right = nullptr;
    }
    // 行くべき方向の深さ
    int depth = getDepth(size);
    // 今どこのノードにいるか
    Node *node = root;
    while (depth--) {
        int way = (size >> depth) & 1;
        Node *&nextNode = way ? node->right : node->left;
        if (nextNode == nullptr) {
            nextNode = new Node();
            *nextNode = appendNode;
            break;
        }
        if (nextNode->value <= appendNode->value) {
            node = nextNode;
        } else {
            // 交換
            Node temp = *nextNode;
            *nextNode = appendNode;
            nextNode->left = temp->left;
            nextNode->right = temp->right;
            appendNode = temp;
            appendNode->left = nullptr;
            appendNode->right = nullptr;
            node = nextNode;
        }
    }
    return;
}
int MyHeap::top() {
    if (root == nullptr) {
        cout << "this tree is empty" << endl;
        return 0;
    }
    return root->value;
}
void MyHeap::pop() {
    // 行くべき方向の深さ
    int depth = getDepth(size);
    Node *node = root;
    while (depth--) {
        int way = (size >> depth) & 1;
        Node *&nextNode = way ? node->right : node->left;
        if (nextNode->left == nullptr) {
            root->value = nextNode->value;
            way ? node->right = nullptr : node->left = nullptr;
            delete nextNode;
            break;
        }
        node = nextNode;
    }
    // Heap再構築
    queue<Node *> que;
    que.push(root);
    while (!que.empty()) {
        Node *node = que.front();
        que.pop();
        if (node == nullptr) break;
        if (node->left && node->right) {
            if (node->left->value < node->right->value) {
                // left smaller
                if (node->left->value < node->value) {
                    // switch
                    int temp = node->value;
                    node->value = node->left->value;
                    node->left->value = temp;
                }
                que.push(node->left);
            } else {
                // right smaller
                if (node->right->value < node->value) {
                    // switch
                    int temp = node->value;
                    node->value = node->right->value;
                    node->right->value = temp;
                }
                que.push(node->right);
            }
        } else if (node->left == nullptr && node->right == nullptr) {
            break;
        } else if (node->left) {
            if (node->left->value < node->value) {
                // switch
                int temp = node->value;
                node->value = node->left->value;
                node->left->value = temp;
            }
            que.push(node->left);
        } else {
            if (node->right->value < node->value) {
                // switch
                int temp = node->value;
                node->value = node->right->value;
                node->right->value = temp;
            }
            que.push(node->right);
        }
    }
    size -= 1;
    if (size == 0) {
        root = nullptr;
    }
    return;
}
bool is_pow2(int x) {
    if (x == 0) {
        return false;
    }
    return (x & (x - 1)) == 0;
}
void MyHeap::display() {
    queue<Node *> que;
    if (root == nullptr) {
        cout << "heap is empty" << endl;
        return;
    }
    que.push(root);
    int cnt = 1;
    while (!que.empty()) {
        Node *node = que.front();
        if (node == nullptr) break;
        que.pop();
        cout << node->value << " ";
        if (is_pow2(cnt + 1)) {
            cout << endl;
        }
        cnt++;
        if (node->left != nullptr) que.push(node->left);
        if (node->right != nullptr) que.push(node->right);
    }
}

テストコード

myHeap.cpp

#include <algorithm>
#include <ctime>
#include <iomanip>
#include <iostream>
#include <random>
#include <vector>

#include "myHeap.h"
using namespace std;
uint64_t get_rand_range(uint64_t min_val, uint64_t max_val) {
    // 乱数生成器
    static std::mt19937_64 mt64(0);

    // [min_val, max_val] の一様分布整数 (int) の分布生成器
    std::uniform_int_distribution<uint64_t> get_rand_uni_int(min_val, max_val);

    // 乱数を生成
    return get_rand_uni_int(mt64);
}
void displayArray(const vector<int> &arr) {
    for (int i = 0; i < arr.size(); i++) {
        cout << arr[i] << " ";
    }
    cout << endl;
}
bool isSorted(const vector<int> &arr) {
    bool flag = true;
    for (int i = 1; i < arr.size(); i++) {
        flag &= arr[i - 1] <= arr[i];
    }
    return flag;
}
int main(void) {
    const int TEST_CASE_SIZE = 100000;
    cout << "test case size : " << TEST_CASE_SIZE << endl;
    cout << endl;
    // init test case
    vector<int> test1;
    vector<int> test2;
    for (int i = 0; i < TEST_CASE_SIZE; i++) {
        test1.push_back(get_rand_range(INT64_MIN, INT64_MAX));
    }
    copy(test1.begin(), test1.end(), back_inserter(test2));

    // MyHeap
    cout << "===== MyHeap =====" << endl;
    MyHeap myHeap = MyHeap();
    if (isSorted(test1)) {
        cout << "sorted" << endl;
    } else {
        cout << "not sorted" << endl;
    }
    int start1 = clock();
    for (int i = 0; i < test1.size(); i++) {
        myHeap.push(test1[i]);
    }
    int middle1 = clock();
    cout << "heap building time: ";
    cout << fixed << setprecision(15) << 1.0 * (middle1 - start1) / CLOCKS_PER_SEC << endl;
    for (int i = 0; i < test1.size(); i++) {
        test1[i] = myHeap.top();
        myHeap.pop();
    }
    int end1 = clock();
    cout << "remove time       : ";
    cout << fixed << setprecision(15) << 1.0 * (end1 - middle1) / CLOCKS_PER_SEC << endl;
    cout << "whole time        : ";
    cout << fixed << setprecision(15) << 1.0 * (end1 - start1) / CLOCKS_PER_SEC << endl;

    if (isSorted(test1)) {
        cout << "sorted" << endl;
    } else {
        cout << "not sorted" << endl;
    }
    cout << endl;
    // heapq
    cout << "===== c++ library =====" << endl;
    if (isSorted(test2)) {
        cout << "sorted" << endl;
    } else {
        cout << "not sorted" << endl;
    }
    int start2 = clock();
    make_heap(test2.begin(), test2.end());
    int middle2 = clock();
    cout << "heap building time: ";
    cout << fixed << setprecision(15) << 1.0 * (middle2 - start2) / CLOCKS_PER_SEC << endl;
    sort_heap(test2.begin(), test2.end());
    int end2 = clock();
    cout << "sort_heap time    : ";
    cout << fixed << setprecision(15) << 1.0 * (end2 - middle2) / CLOCKS_PER_SEC << endl;
    cout << "whole time        : ";
    cout << fixed << setprecision(15) << 1.0 * (end2 - start2) / CLOCKS_PER_SEC << endl;
    if (isSorted(test2)) {
        cout << "sorted" << endl;
    } else {
        cout << "not sorted" << endl;
    }
    cout << endl;
    // time diff
    cout << "whole time diff" << endl;
    cout << fixed << setprecision(15) << 1.0 * abs((end1 - start1) - (end2 - start2)) / CLOCKS_PER_SEC << endl;
    cout << "whole time ratio (MyHeap/library)" << endl;
    cout << fixed << setprecision(15) << 1.0 * (end1 - start1) / (end2 - start2) << endl;

    cout << endl;
    return 0;
}

実行

$ g++ test.cpp myHeap.cpp
$ ./a.out
test case size : 100000

===== MyHeap =====
not sorted
heap building time: 0.021775000000000
remove time       : 0.160527000000000
whole time        : 0.182302000000000
sorted

===== c++ library =====
not sorted
heap building time: 0.007654000000000
sort_heap time    : 0.068640000000000
whole time        : 0.076294000000000
sorted

whole time diff
0.106008000000000
whole time ratio (MyHeap/library)
2.389467061630010

時間計算量

結果より、ポインタを用いたヒープは配列を用いた場合の2~3倍くらいかそれ以上かかりますね。
TEST_CASE_SIZEが小さい(100とか)場合はその差が顕著です。

push1回あたりlog2(n)
heapに追加するのにpushをn回呼ぶ
ヒープ構築作業でnlog2(n)

topはO(1)

pop1回あたり2log2(n)
pop呼び出しがn回
要素の取り出しで2nlog2(n)

以上あわせて
3nlog2(n)
といったところでしょうかね。

配列ヒープは最悪時間計算量nlog2(n)なので、まぁこんなもんじゃないでしょうか。

ポインタを用いたヒープで、要素の取り出しをlog2(n)で実装する方法を思いついた有能な方は是非教えて下さい。

参考