Abstract
for文と対応するNumpyの記述を公式っぽく記述しながら、書き方のパターンを列挙していく形で進行します。半分くらい自分用です。
導入
「PythonのFor文は遅いからNumpyで書いた方が速いで。」
しかしながら、for文を殲滅するのは特に初学者にとって鬼門です。スケールが大きくない場合はそれでも良いですが、機械学習系の処理などはデータ量が多いためO(N^2)でも目に見えて遅くなります。
また初歩的なブロードキャストを理解できて2重ループは殲滅できても、3次元以上になると途端に複雑になりがちです。そこで本記事では特に2次元以上のケースにスポットを当てて、パターンを紹介していこうと思います。
本記事ではまず、ブロードキャストについて解説します。その後np.sumやnp.dotを駆使して、様々なパターンでfor文を殲滅していきます。
用語定義 / 前提知識
Numpyは以下のようにimportし、乱数発生器としてseed = 64でrngを定義します。
import numpy as np
rng = np.random.default_rng(64)
| 用語 | 意味 |
|---|---|
| numpy配列 |
np.ndarrayのこと。np.array(), np.arange()とかで生成したオブジェクトのこと。 |
| Numpy化, Numpify | for文をnumpy配列の計算に置き換えること。 |
基本的にはパッケージとして言及する場合はNumpy, プログラム中で言及する時(numpy配列など)はnumpyで記述しようとは思いますが、多分間違えるので気にしないでください。
ブロードキャスト基本編
このセクションでは、2次元以下の配列に関するブロードキャストを扱います。
ブロードキャストとは、サイズ或いは次元が異なるnumpy配列の演算を拡張して行うような仕組みのことです。
まず最も基本的な例として、定数と1次元配列の演算が挙げられます。
#* for文 *#
x = np.arange(5)
a = 2
y = np.zeros_like(x)
for i in range(5):
y[i] = a * x[i]
print(y) # [0 2 4 6 8]
#* numpy化 *#
y = a * x
print(y) # [0 2 4 6 8]
定数とnumpy配列を演算した場合、基本的には各要素に対して演算が行われるように処理されます。これは+, -, *, /, //, %など基本の算術演算子はそうなります。==などの比較演算子も、基本的には各要素に対して比較します。
しかしながら、この先のブロードキャストを理解するには、各要素に対しての演算というよりは、公式ドキュメントのような理解が大切です。
(https://numpy.org/doc/stable/user/basics.broadcasting.html figure 1より)
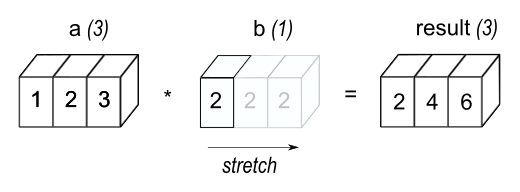
図はnp.array([1, 2, 3]) * 2 = np.array([2, 4, 6])を表した模式図です。
演算する際には足りない要素を補うようにしてコピーが作成され、そのあと演算を行うようなイメージです。
1次元配列同士の場合
では1次元配列同士ではどうでしょうか。
これも要素数が同じなら、各要素で対応して演算します。
x = np.arange(5)
y = np.arange(5, 10) # array([5, 6, 7, 8, 9])
z = np.zeros_like(x)
#* for *#
for i in range(5):
z[i] = x[i] * y[i]
print(z) # [ 0 6 14 24 36]
#* numpy化 *#
z = x * y
print(z) # [ 0 6 14 24 36]
なお、要素数が異なる場合エラーになります。
x = np.arange(5)
y = np.arange(5, 9)
z = x * y
# Traceback (most recent call last):
# File "<stdin>", line 1, in <module>
# ValueError: operands could not be broadcast together with shapes (5,) (4,)
比較演算子の場合、要素数が異なっていてもエラーは出ません(2022/04/26現在)が、将来的にはエラーになるようです。
x == y # `False`となる。
# __main__:1: DeprecationWarning: elementwise comparison failed; this will raise an error in the future.
2次元配列の場合
このセクションではまずいわゆるベクトル(shapeの片方が1次元)同士について見た後、その後行列(shapeが(2, 2)など)について見ていきます。
まず、どちらも列ベクトルである場合は先ほどの1次元の場合とほとんど同じです。
つまり各要素に対して演算を行います。
x = np.arange(5).reshape((-1, 1))
# array([[0],
# [1],
# [2],
# [3],
# [4]])
y = np.arange(5, 10).reshape((-1, 1))
# array([[5],
# [6],
# [7],
# [8],
# [9]])
z = np.zeros_like(x)
#* for *#
for i in range(5):
z[i, 0] = x[i, 0] * y[i, 0]
print(z)
# [[ 0]
# [ 6]
# [14]
# [24]
# [36]]
#* numpy化 *#
z = x * y
print(z)
# [[ 0]
# [ 6]
# [14]
# [24]
# [36]]
要素数が異なる場合エラーになります。
では列ベクトルと行ベクトルの場合はどうなるのかというと
x = np.arange(5).reshape((-1, 1))
# array([[0],
# [1],
# [2],
# [3],
# [4]])
y = np.arange(5, 10).reshape((1, -1))
# array([[5, 6, 7, 8, 9]])
z = np.zeros((5, 5))
#* for *#
for i in range(5):
for j in range(5):
z[i, j] = x[i, 0] * y[0, j]
print(z)
# [[ 0. 0. 0. 0. 0.]
# [ 5. 6. 7. 8. 9.]
# [10. 12. 14. 16. 18.]
# [15. 18. 21. 24. 27.]
# [20. 24. 28. 32. 36.]]
#* numpy化 *#
z = x * y
print(z) # 上の出力と同じ
イメージは以下のようになります。
ちなみに1次元配列とベクトルの場合、1次元配列は横ベクトル(行ベクトル)のような扱いになります。
>>> x = np.arange(3).reshape((-1, 1))
>>> y = np.arange(3, 6)
>>> x
array([[0],
[1],
[2]])
>>> y
array([3, 4, 5])
>>> x*y
array([[ 0, 0, 0],
[ 3, 4, 5],
[ 6, 8, 10]])
続いて、行列についても見ていきます。
A = np.arange(4).reshape((-1, 1)) * (np.ones(3) * 10)
b = np.arange(3)
c = np.zeros((4, 3))
#* for *#
for i in range(4):
for j in range(3):
c[i, j] = A[i, j] + b[j]
print(c)
# array([[ 0., 1., 2.],
# [10., 11., 12.],
# [20., 21., 22.],
# [30., 31., 32.]])
#* numpify *#
c = A + b
print(c) # ↑と同じ出力
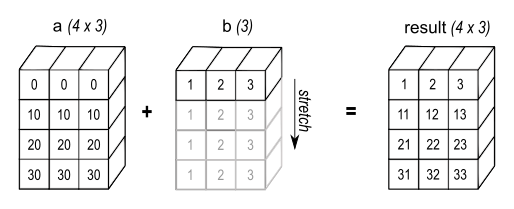
こちらは以下の画像のイメージ。
(https://numpy.org/doc/stable/user/basics.broadcasting.html figure 2より)
ここで注意したいのが、ブロードキャストの条件です(ようやく登場)。
ここまで理解できると、ブロードキャストが可能なのは最後のshapeが同じか1の時だと勘付くでしょう。
実際以下のように、shapeが異なるとエラーになります。

(https://numpy.org/doc/stable/user/basics.broadcasting.html figure 3より)
shapeの最後が1の時は以下のようになります。
ブロードキャスト応用編
このセクションでは3次元の配列(高階テンソル)のブロードキャストについて扱います。
先ほど「ブロードキャストが可能なのは最後のshapeが同じか1の時だと勘付くでしょう。」と言いましたがこれは正確ではありません。公式(https://numpy.org/doc/stable/user/basics.broadcasting.html#general-broadcasting-rules)では以下のように述べられています。
When operating on two arrays, NumPy compares their shapes element-wise. It starts with the trailing (i.e. rightmost) dimensions and works its way left. Two dimensions are compatible when
they are equal, or
one of them is 1
つまり:shapeを後ろから比べ、同じならその軸はスルーして、1なら1じゃない方に合わせる。これを繰り返して同じshapeになったら計算を各要素に対して実行する。といった流れになります。
試しに以下を見てみましょう。
A = np.arange(8).reshape((2, 2, 2))
# array([[[0, 1],
# [2, 3]],
# [[4, 5],
# [6, 7]]])
B = np.arange(4).reshape((2, 1, 2))
# array([[[0, 1]],
# [[2, 3]]])
C_for = np.zeros_like(A)
for i in range(2):
for j in range(2):
for k in range(2):
C_for[i, j, k] = A[i, j, k] + B[i, 0, k]
print(C_for)
C = A + B
print(C)
# C_forもCも以下。
# [[[ 0 2]
# [ 2 4]]
# [[ 6 8]
# [ 8 10]]]
イメージは以下のようになります。
ブロードキャスト完全に理解しましたね。
ブロードキャストの例は他にも紹介されています。
(https://numpy.org/doc/stable/user/basics.broadcasting.html#broadcastable-arrays)
ここまで理解できるていると公式の例もすんなり理解できると思います。
for文殲滅戦略
実際ブロードキャストを理解すると多くの計算を効率化できますが、for文で計算する用途として和を計算するパターンも多いでしょう。そこで本セクションでは、np.sumやnp.dotなどを駆使したfor文の置換パターンを紹介します。
基本パターン
要素毎に何か操作をして和をとる場合は、その要素に操作を加えた後np.sum或いはndarray.sumを使いましょう。
\boldsymbol{x} = [ x_1 \ x_2 \ \cdots \ x_N ]^T \\
e = \sum_{i = 1}^N x_i^2
N = 5
x = rng.uniform(0, 1, (N, 1))
e_for = 0
for i in range(N):
e_for += x[i, 0]**2
print(e_for)
#* numpify *#
e = np.power(x, 2).sum()
# e = np.sum(x**2)) など
print(e)
内積パターン
\boldsymbol{x} = [ x_1 \ x_2 \ \cdots \ x_N ]^T \\
\boldsymbol{y} = [ y_1 \ y_2 \ \cdots \ y_N ]^T \\
e = \sum_{i = 1}^N x_i y_i
N = 5
x = rng.uniform(0, 1, (N, ))
y = rng.uniform(0, 1, (N, ))
e_for = 0
for i in range(N):
e_for += x[i] * y[i]
print(e_for)
#* numpify *#
e = np.dot(x, y)
print(e)
並列計算パターン
内積パターンが行列などの成分になっているパターンです。
$f_j(x)$は適当な関数で、$\boldsymbol{x} = [x_1 \ \cdots \ x_N]^T$とします。
以下の$e$を求めます。
\boldsymbol{e} = \begin{bmatrix}
\sum_{i = 1}^N x_i f_1(x_i) \\
\sum_{i = 1}^N x_i f_2(x_i) \\
\vdots \\
\sum_{i = 1}^N x_i f_M(x_i)
\end{bmatrix}
for文で書き下すと次のようになります。
def f(j, x):
return j * x
N = 5
M = 3
x = rng.uniform(0, 1, (N, 1))
e_for = np.zeros((M, 1))
for j in range(M):
e_for[j] = 0
for i in range(N):
e_for[j] += x[i, 0] * f(j, x[i, 0])
# or
# e_for[j] = np.dot(x, f(j, x))
ではnumpifyしていきます。まずは$\boldsymbol{e}$の各要素を眺めます。これは先ほどのパターンですね。
\sum_{i = 1}^N x_i f_j(x_i) = \begin{bmatrix}
f_j(x_1) & \cdots & f_j(x_N)
\end{bmatrix}\begin{bmatrix}
x_1 \\
\vdots \\
x_N
\end{bmatrix} \\
$j$と$i$が分離できました。
ここで$j$の方向(列方向)に$[ f_j(x_1) \ \cdots \ f_j(x_N) ]$を並べて新たな行列を定義してみると
F(x) := \begin{pmatrix}
f_1(x_1) & \cdots & f_1(x_N) \\
&\vdots& \\
f_j(x_1) & \cdots & f_j(x_N) \\
&\vdots& \\
f_M(x_1) & \cdots & f_M(x_N)
\end{pmatrix}
$$
\boldsymbol{e} = F(x)\boldsymbol{x}
$$
となりますね。よって以下のように実装できます。
def F(x):
# ここは本来実装に応じて更に高速化する。
# 通常のforより内包表記の方が速い。
return np.concatenate([
f(j, x).reshape((1, -1)) for j in range(M)
])
e = F(x).dot(x)
print(e)
まとめ
ブロードキャストを完全に理解することは難しくても、ある程度パターンを理解できればそのうち色々なパターンにも対応できるかなーと思って、自分の理解をまとめてみた記事です。
まだネタはあるのですが、多忙につきとりあえず書けていた部分で投稿しました。時間があって気が向いたら追記していきます。
間違いがあればご指摘お願いします。