はじめに
短時間フーリエ変換とその逆変換についての備忘録.
数式も英語も碌に読めない素人の独学なので内容の正確性は保証しない.
例として挙げるコードは C# で書く.
また、コード中で複素数を表す型 Complex は System.Numerics.Complex である.
spectrum に対応する日本語としては スペクトラム を使用する.
一般的にはフランス語の spectre 由来で スペクトル と呼ばれることが多いのだが、コード中は spectrum であるし、参考文献も読んで精々英語であるためまあいいかなって.
フーリエ変換(FT, Fourier Transform)
短時間フーリエ変換に至る前に、まずは単純なフーリエ変換のイメージをつかむ必要がある.
YouTube の以下の動画が視覚的で、イメージをつかむにはよい.
離散フーリエ変換(DFT, Discrete Fourier Transform) とその逆変換
上記のフーリエ変換は時間が連続(実数)であったが、通常コンピューターで扱う音声データはデジタル(離散的)である.
多くの場合 double[] のような配列で表現されるように、時間は整数で指定するから、動画のような積分ではなく総和(Σ)で扱うことになる.
それだけと言えばそれだけなのだが、その辺りの違いでフーリエ変換一族は多岐にわたるので体系的に学ぼうとするとややこしい.
離散フーリエ変換(DFT)
音声データが関数 x(t) で表現される場合、その離散フーリエ変換 F(f) = DFT(x)(f) は以下のような数式となる:
F(f) = \sum_{t=0}^{N-1}x(t)e^{-2 \pi i f t / N}
ただし、N は音声データの長さ.
コードにすると以下(数式中の x に代えて waveform を使用):
/// <summary>
/// 離散フーリエ変換を行う
/// </summary>
/// <param name="waveform">波形データ</param>
/// <returns>スペクトラム</returns>
public static Complex[] DFT(Complex[] waveform) {
int N = waveform.Length;
Complex[] spectrum = new Complex[N];
for (int f = 0; f < N; ++f) {
Complex v = Complex.Zero;
for (int t = 0; t < N; ++t) {
double z = -2 * Math.PI * f * t / N;
// オイラーの公式より、exp(iz) = cos(z) + i sin(z)
double real = Math.Cos(z);
double imag = Math.Sin(z);
v += waveform[t] * new Complex(real, imag);
}// loop for t, in [0 .. N)
spectrum[f] = v;
}// loop for f, in [0 .. N)
return spectrum;
}// DFT(Complex[] waveform)
コード中では波形データを複素数型にしている. もしも double[] を使う場合は以下の関数を通すこと:
public static Complex[] ToComplex(double[] realwave) {
int N = waveform.Length;
Complex[] compwave = new Complex[N];
for (int t = 0; t < N; ++t) {
double real = realwave[t];
double imag = 0.0;
compwave[t] = new Complex(real, imag);
}// loop for t, in [0 .. N)
return compwave;
}// ToComplex(double[] realwave)
逆離散フーリエ変換(Inverse DFT)
名前の通り DFT の逆変換であり、IDFT(DFT(x)) = x である.
スペクトラムが関数 F(f) である場合、その逆離散フーリエ変換 x(t) = IDFT(f)(t) は以下のような数式となる:
x(t) = \frac{1}{N}\sum_{f=0}^{N-1}F(f)e^{2 \pi i t f / N}
ただし、N はスペクトラムのビンの数.
e の右肩の符号と、全体にかかる 1/N の2点以外は離散フーリエ変換と同じである.
コードにすると以下(数式中の x に代えて waveform を使用):
/// <summary>
/// 逆離散フーリエ変換を行う
/// </summary>
/// <param name="spectrum">スペクトラム</param>
/// <returns>波形データ</returns>
public static Complex[] IDFT(Complex[] spectrum) {
int N = spectrum.Length;
Complex[] waveform = new Complex[N];
for (int t = 0; t < N; ++t) {
Complex v = Complex.Zero;
for (int f = 0; f < N; ++f) {
double z = 2 * Math.PI * t * f / N;// DFT との違いそのいち
// オイラーの公式より、exp(iz) = cos(z) + i sin(z)
double real = Math.Cos(z);
double imag = Math.Sin(z);
v += spectrum[f] * new Complex(real, imag);
}// loop for f, in [0 .. N)
waveform[t] = v / N;// DFT との違いそのに
}// loop for t, in [0 .. N)
return waveform;
}// IDFT(Complex[] spectrum)
ほとんど DFT と同じコードをもう一度書く代わりに、以下のような実装を用いることもできる:
/// <summary>
/// 逆離散フーリエ変換を行う
/// </summary>
/// <param name="spectrum">スペクトラム</param>
/// <returns>波形データ</returns>
public static Complex[] IDFT(Complex[] spectrum) {
int N = spectrum.Length;
Complex[] conj = new Complex[N];
// スペクトラムの共役をとる
for (int i = 0; i < N; i++) {
conj[i] = Complex.Conjugate(spectrum[i]);
}
// DFT を行う
Complex[] waveform = DFT(conj);
// 得られた波形の共役を取り、正規化する
for (int i = 0; i < N; i++) {
waveform[i] = Complex.Conjugate(waveform[i]) / N;
}
return waveform;
}// IDFT(Complex[] spectrum)
バリエーション
離散フーリエ変換は時間領域から周波数領域への変換ができればよく、逆離散フーリエ変換は離散フーリエ変換の逆変換でありさえすればよいため、細かなバリエーションが存在する.
前々節、前節での変換の式において e の右肩の符号は DFT の場合プラス、IDFT の場合マイナスであったが、これは互いに異なりさえすれば逆の組み合わせでもよい.
また、右辺の全体に、DFT では何もかけず、IDFT では 1/N をかけていたけれど、両者に $\frac{1}{\sqrt{N}}$ をかける派閥も存在するらしい.
以上から、少なくとも都合4通りのバリエーションがあるようだ.
この記事では前々節、前節で書いたものに従うが、別の文献を読む場合はそこでどのような定義が採用されているかへの注意をすべき.
高速フーリエ変換(FFT, Fast Fourier Transform) とその逆変換
高速フーリエ変換は数ある〇〇変換一族のメンバーではなく、DFT を高速で行うためのアルゴリズムである.
そのため、(計算効率を度外視すれば)上で示した DFT/iDFT と同一視できる.
まあ FFT/iFFT でなければ実用に耐えない処理が多すぎるのだけれど.
真面目に解説しようとするとそれだけでひとつの記事になりそうなトピックなので、深入りはしない.
FFT/iFFT の実装は探せば比較的簡単に見つかるが、ここには最も単純な Cooley–Tukey FFT を示す(正直に言うと ChatGPT に書いてもらった).
これは長さが2の冪であるデータしか扱えないので、例えば長さが 1000 のデータを扱うなら 2^10 = 1024 になるようゼロパディングするなどしてから使用する.
逆変換は iDFT の節のふたつ目のコードで DFT を FFT に代えるか、別途探してほしい.
/// <summary>
/// 離散フーリエ変換を行う
/// </summary>
/// <param name="waveform">長さが2の冪であるような波形データ</param>
/// <returns>スペクトル</returns>
public static Complex[] FFT(Complex[] waveform) {
int n = waveform.Length;
Complex[] spectrum = new Complex[n];
int m = (int) (Math.Log(n) / Math.Log(2));
Complex[] rev = new Complex[n];
for (int i = 0; i < n; i++) {
int j = ReverseBits(i, m);
rev[j] = waveform[i];
}
for (int s = 1; s <= m; s++) {
int l = 1 << s;
Complex wn = Complex.FromPolarCoordinates(1, -2 * Math.PI / l);
for (int k = 0; k < n; k += l) {
Complex w = Complex.One;
for (int j = 0; j < l / 2; j++) {
Complex t = w * rev[k + j + l / 2];
Complex u = rev[k + j];
spectrum[k + j] = u + t;
spectrum[k + j + l / 2] = u - t;
w *= wn;
}
}
for (int i = 0; i < n; i++)
rev[i] = spectrum[i];
}
return spectrum;
}// FFT(Complex[] waveform)
private static int ReverseBits(int n, int m) {
int rev = 0;
for (int i = 0; i < m; i++) {
rev <<= 1;
rev |= (n & 1);
n >>= 1;
}
return rev;
}// ReverseBits(int n, int m)
窓関数
DFT は渡された波形データが1周期分である周期関数であるものとして結果を返す.
渡した波形データの頭と尻尾が一致しないような場合はきれいな結果にならず、ときには不都合もある.
そのため、多くの場合では窓関数を掛けてから処理が行われる.
窓関数は驚くほど多くの種類があるが、最も基本的な窓関数のひとつであるハン窓(ハニング窓)のコードを示す:
public static double[] CreateHannWindow(int frameSize) {
double[] window = new double[frameSize];
for (int i = 0; i < frameSize; i++) {
window[i] = 0.5 - 0.5 * Math.Cos(2 * Math.PI * i / frameSize);
}
return window;
}// CreateHannWindow(int frameSize)
あえて用意するようなものでもないと思うが、窓を掛ける処理:
public static Complex[] Windowing(Complex[] waveform, double window) {
int frameSize = waveform.Length;
Complex[] windowed = new Complex[frameSize];
for(int i = 0; i < frameSize; ++i) {
windowed[i] = waveform[i] * window[i];
}
return windowed;
}// Windowing(Complex[] waveform, double window)
短時間フーリエ変換(STFT, Short Time Fourier Transform)
音声信号を解析する場合、「この瞬間におけるこの周波数成分はうんたらかんたら」という話をしたいため、数分間ある音声データを丸ごと DFT しても意味がない(「この瞬間」という情報が消えるため).
したがって、音声解析においては「0-100ミリ秒の区間のスペクトラム」、「50-150ミリ秒の区間のスペクトラム」、「100-200ミリ秒の区間のスペクトラム」... のように短い区間へと分割し DFT したものを用いる.
この処理は単純に「解析(Analysis)」の語で片づけられることもあるが、STFT という名前が付けられている.
こうして得られたスペクトラムの束を指してスペクトログラム (spectrogram) と呼ぶ.
これに必要なものとしては、対象の波形データ、各区間の長さ、DFT のための窓関数、前の区間から次の区間までの時間差、のよっつ(窓関数を配列として渡して、その長さ = 各区間の長さ とすれば引数はみっつ).
または、「前の区間から次の区間までの時間差」の代わりに「前の区間との重複部分の長さ」を要求する流派もある.
通常
「前の区間から次の区間までの時間差」= 「各区間の長さ」 - 「前の区間との重複部分の長さ」
なので、些細な問題.
この記事で使用する語
「各区間」、または「各区間の波形データ」はフレーム (frame) やチャンク (chunk) などと呼ばれる.
この記事ではフレーム (frame) を採用する.
「前の区間から次の区間までの時間差」はシフト量 (shift size, - length) や ホップサイズ (hop size)、ずらし量などと呼ばれる.
この記事ではずらし量 (hop size) を採用する.
シフトはともかくホップは日本語としてあまり使わないので違和感が拭えない... .
英語では hop size が一番使われるように思う.
フレームへの分割
(これ要る?)
入力された波形データをフレームに分割する.
余った部分はたいていゼロパディングで処理される.
以下の図において、一番上にあるのが入力された波形データ、下2段が分割されたフレームたちである.
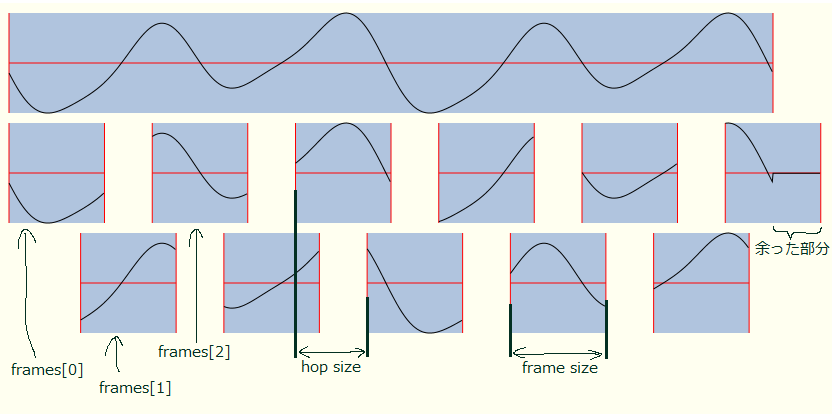
上の例ではフレームが小さすぎるだろうが、分割方法の例なので.
コード例
分割さえできればあとは窓を掛けて DFT するだけなので説明不要だろう.
以下のコードでは frames と spectrogram として異なる配列を用意しているけれど、説明のためそうしているだけで分ける意味はほとんどない.
ついでに言えばループを分ける意味も薄い.
/// <summary>
/// 短時間フーリエ変換を行う
/// </summary>
/// <param name="waveform">波形データ</param>
/// <param name="frameSize">フーリエ変換を行う窓の長さ</param>
/// <param name="hopSize">各フレームのずらし量</param>
/// <param name="window">窓関数の値(長さが frameSize である配列)</param>
/// <returns>スペクトログラム</returns>
public static Complex[][] STFT(Complex[] waveform, int frameSize, int hopSize, double[] window) {
int numFrames = (int) Math.Ceiling((waveform.Length - frameSize) / (double) hopSize) + 1;
// フレームへ分割し、窓を掛ける
Complex[][] frames = new Complex[numFrames][];
for (int i = 0; i < numFrames; i++) {
int start = i * hopSize;
Complex[] frame = new Complex[frameSize];
// 最後のフレームが waveform をはみ出すかもしれないので [start + j < waveform.Length] で判定する
for (int j = 0; (j < frameSize) && (start + j < waveform.Length); ++j) {
// 窓を掛ける
frame[j] = waveform[start + j] * window[j];
}
frames[i] = frame;
}
// 最後のフレームについて、waveform からはみ出した部分を 0 で埋める.
// 明示的に書く必要がない説はある.
// frames[numFrames - 1] は waveform[start = (numFrames - 1) * hopSize] から長さ frameSize の区間
// frames[numFrames - 1] の内、実際に要素が入っている長さは actualLength = waveform.Length - start
// したがって、はみ出した部分の長さは frameLength - actualLength
for (int j = frameSize - waveform.Length - (numFrames - 1) * hopSize; j > 0; --j) {
// 後ろ側を 0 で埋める
frames[numFrames - 1][frameSize - j] = Complex.Zero;
}
// すべてのフレームについて DFT を行う
Complex[][] spectrogram = new Complex[numFrames][];
for (int i = 0; i < numFrames; i++) {
spectrogram[i] = DFT(frames[i]);
}
return spectrogram;
}// STFT(Complex[] wave, int frameSize, int hopSize, double[] window)
逆短時間フーリエ変換(iSTFT, Inverse STFT)
STFT が「合成(Analysis)」と呼ばれるのに対応して、単純に「合成(Synthesis)」とか「再合成(Resynthesis)」みたいに呼ばれることもあるが、「STFT」の語を使った場合は Inverse STFT の名前が出てくる.
名前の通り STFT の逆変換であり、STFT でゼロパディングされる部分は無視して ISTFT(STFT(x)) = x である.
単純に考えれば、STFT の手順を逆にたどって
- 各スペクトラムについて IDFT を行う
- 得られた各フレームを窓関数で割る
- 重複部分を考慮していい感じにデータを拾う
のようになるが、この場合手順 3 にいくらでもパターンが考えられる.
「frames[0] のデータをすべて拾い、以降は前のフレームに重複する部分を捨て残りを拾う」とか
反対に、「後ろのフレームに重複する部分を捨てて残りを拾う」とか
「重複する部分について、重複しているすべてのフレームの平均を取る」とか.
どれも結局同じことのように思えるが、ISTFT を使うのはたいてい「STFT で得られたスペクトログラムを編集することで得た新しいスペクトログラムから波形データを生成したい」場合であるため、重複しているフレームで波形が必ずしも一致しない.
以上から、ISTFT は、あるスペクトログラム spec について STFT(ISTFT(spec)) = spec であってほしい.
しかし編集されたスペクトログラムに対しては常に = であるような ISTFT が存在しないため、両辺の二乗誤差が最小であるような変換であると定義される.
数式変形については正直よくわからないが、参考文献「Invertibility of overlap-add processing」によると ISTFT は次のように書けるらしい:
x[n] = \frac{\sum_t{y_t[n] w^a[n - tH]}}{\sum_t{w^{a + 1}[n - tH]}}
ここで、
x[n] が復元された波形データ
t がフレーム/スペクトラムのインデックス
y_t が t 番目のスペクトラムを DFT したもの
w が窓関数
H がフレームのずらし量 (hop size)
a はパラメータで、a = 1 が一番いい感じらしい
ただし、y_t はこの記事の STFT で書いたようなフレームとは少し形が違う.
参考文献「MathWorks」の一番下の図が多分それ.
上で単純に考えた、ISTFT の手順の内「2. 得られた各フレームを窓関数で割る」と「3. 重複部分を考慮していい感じにデータを拾う」がひっくるめられたようなものだろうか.
/// <summary>
/// 逆短時間離散フーリエ変換を行う
/// </summary>
/// <param name="spectrogram">スペクトログラム</param>
/// <param name="frameSize">フーリエ変換を行った窓の長さ</param>
/// <param name="hopSize">各フレームのずらし量</param>
/// <param name="window">STFTに利用した窓関数の値(長さが frameSize である配列)</param>
/// <returns>波形データ</returns>
public static Complex[] ISTFT(Complex[][] spectrogram, int frameSize, int hopSize, double[] window) {
int numFrames = spectrogram.Length;
// 合成される波形データの長さ
int L = (numFrames - 1) * hopSize + frameSize;
Complex[] waveform = new Complex[L];
// 分母部分. 合成後の正規化係数(?)
double[] wsum = new double[L];
for (int i = 0; i < L; ++i) {
waveform[i] = Complex.Zero;
wsum[i] = 0;
}
// すべて IDFT して足し合わせる
for (int i = 0; i < numFrames; ++i) {
int start = i * hopSize;
// IDFT する
Complex[] frame = IDFT(spectrogram[i]);
for (int j = 0; j < frameSize; ++j) {
double w = window[j];
// このフレームの波形に窓を掛けてから足す
waveform[start + j] += frame[j] * w;
// ついでにスケーリング用の係数を求める
wsum[start + j] += w * w;
}
}
// scaling
for (int i = 0; i < L; ++i) {
// 0 で割ると NaN になるので避ける
if (wsum[i] != 0) {
waveform[i] /= wsum[i];
}
}
return waveform;
}// ISTFT(Complex[][] spectrogram, int frameSize, int hopSize, float[] window)
参考文献
YouTube "But what is the Fourier Transform? A visual introduction."
Wikipedia 離散フーリエ変換
小野順貴さんによる解説 「短時間フーリエ変換の基礎と応用」https://www.jstage.jst.go.jp/article/jasj/72/12/72_764/_pdf
MathWorks 日本 「逆短時間フーリエ変換」https://jp.mathworks.com/help/signal/ref/istft_ja_JP.html
「Invertibility of overlap-add processing」https://gauss256.github.io/blog/cola.html
stackoverflow (Basj さんの回答) https://stackoverflow.com/questions/2459295/invertible-stft-and-istft-in-python
はてなブログ「音楽プログラミングの超入門(仮)」 https://yukara-13.hatenablog.com/entry/2013/11/17/210204