Pythonでアルゴリズム（幅優先探索、bfs）

#はじめに
　pythonを使った幅優先探索の実装について解説していきます。（僕がいつも実装するやつを載せるだけです。）
　幅優先探索ではよく距離についての問題が出てくるので、今回はある1頂点から各頂点までの距離を返す関数を実装します。
#幅優先探索
　幅優先探索に関する一般的な知識は調べればたくさん出てくると思うので、詳しくは省略しますが簡単に説明します。
　　　
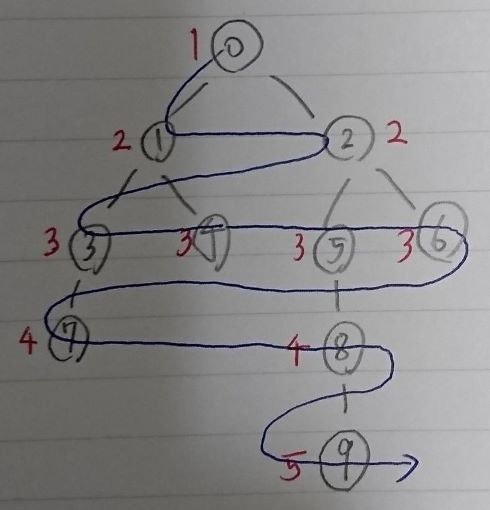
　青い矢印のように、近いところから順に頂点を追っていきます。今回扱う距離の場合には、ひとつ前の頂点までの距離に1を足せばいいです。（画像では1から振っていますが、距離ならば0から振ればいいです。）
　この頂点の探索の順番は、キューで管理します。キューは、先入れ先出しのデータ構造です。今回の例でいうと、まずはスタートの0が入ります。（[0]）次に、中身を前から取り出し、隣接する頂点を調べます。（今回は1, 2）初めて訪れたのであればキューに追加します。（[1, 2]）
　これを繰り返していけば青い矢印順に頂点を調べることができます。
（[2, 3, 4]→[3, 4, 5, 6]→[4, 5, 6, 7]...）
　キューが空になったら探索終了です。お疲れ様です。
#実装
##入力
　頂点数nと辺の数mが与えられ、その後隣接する頂点をm行に渡って与えられます。

11 9
0 1
0 2
1 3
1 4
2 5
2 6
3 7
5 8
8 9

##コード

import sys
input = sys.stdin.readline

n, m = [int(x) for x in input().split()] # nは頂点の数、mは辺の数
g = [[] for _ in range(n)] # 隣接リスト

for _ in range(m):
    a, b = [int(x) for x in input().split()]
    g[a].append(b)
    g[b].append(a)

from collections import deque

def bfs(u):
    queue = deque([u])
    d = [None] * n # uからの距離の初期化
    d[u] = 0 # 自分との距離は0
    while queue:
        v = queue.popleft()
        for i in g[v]:
            if d[i] is None:
                d[i] = d[v] + 1
                queue.append(i)
    return d

# 0からの各頂点の距離
d = bfs(0)
print(d)

##出力
左から頂点の番号順に頂点0との距離を持つリストを出力します。自分との距離は0で、たどり着けない頂点はNoneとなります。

[0, 1, 1, 2, 2, 2, 2, 3, 3, 4, None]

#おわりに
　何か間違いがあれば是非教えてください！アドバイスなどもいただけたらうれしいです！