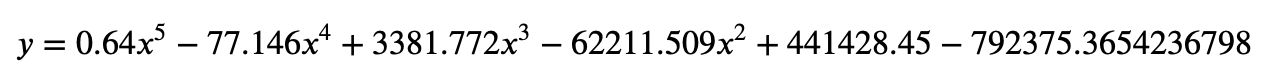概要(TL;DR)
前回、データの確認を終えたので、次は数式モデルを算出する。
(現在 勉強中なので間違い等をどんどん指摘してもらえたら嬉しいです。)
DQウォークのレベルアップに必要な経験値の数式モデルを求める(1)
回帰分析
まずは必要なライブラリ郡を取り込む
import pandas as pd
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import linear_model
sns.set()
%matplotlib inline
%precision 3
データをread_csv()で取り込む。
df = pd.read_csv('data.csv',names=['EXP'])
df['CUMSUM_EXP'] = df['EXP'].cumsum()
df.index = df.index + 1
df.head()

sklearnのlinear_modelにデータを食わせる
まずは次のレベルまでに必要な経験値
reg = linear_model.LinearRegression()
X = df.index
Y = df['EXP']
# 予測モデルを作成
reg.fit(X, Y)
# 回帰係数
print(reg.coef_)
# 切片
print(reg.intercept_)
# R2(決定係数)
print(reg.score(X, Y))
jupyterの実行結果にいてつくエラーがほとばしる!!
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-54-69fa63dab1be> in <module>
6 Y = df['EXP']
7 # 予測モデルを作成
----> 8 reg.fit(X, Y)
9 # 回帰係数
10 print(reg.coef_)
/usr/local/lib/python3.7/site-packages/sklearn/linear_model/base.py in fit(self, X, y, sample_weight)
461 n_jobs_ = self.n_jobs
462 X, y = check_X_y(X, y, accept_sparse=['csr', 'csc', 'coo'],
--> 463 y_numeric=True, multi_output=True)
464
465 if sample_weight is not None and np.atleast_1d(sample_weight).ndim > 1:
/usr/local/lib/python3.7/site-packages/sklearn/utils/validation.py in check_X_y(X, y, accept_sparse, accept_large_sparse, dtype, order, copy, force_all_finite, ensure_2d, allow_nd, multi_output, ensure_min_samples, ensure_min_features, y_numeric, warn_on_dtype, estimator)
717 ensure_min_features=ensure_min_features,
718 warn_on_dtype=warn_on_dtype,
--> 719 estimator=estimator)
720 if multi_output:
721 y = check_array(y, 'csr', force_all_finite=True, ensure_2d=False,
/usr/local/lib/python3.7/site-packages/sklearn/utils/validation.py in check_array(array, accept_sparse, accept_large_sparse, dtype, order, copy, force_all_finite, ensure_2d, allow_nd, ensure_min_samples, ensure_min_features, warn_on_dtype, estimator)
519 "Reshape your data either using array.reshape(-1, 1) if "
520 "your data has a single feature or array.reshape(1, -1) "
--> 521 "if it contains a single sample.".format(array))
522
523 # in the future np.flexible dtypes will be handled like object dtypes
ValueError: Expected 2D array, got 1D array instead:
array=[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
49 50 51 52 53 54 55].
Reshape your data either using array.reshape(-1, 1) if your data has a single feature or array.reshape(1, -1) if it contains a single sample.
どうやら、Xは2DのArrayを求めているらしい。確かにsklearnのリファレンスにも下記の様に書いてある。
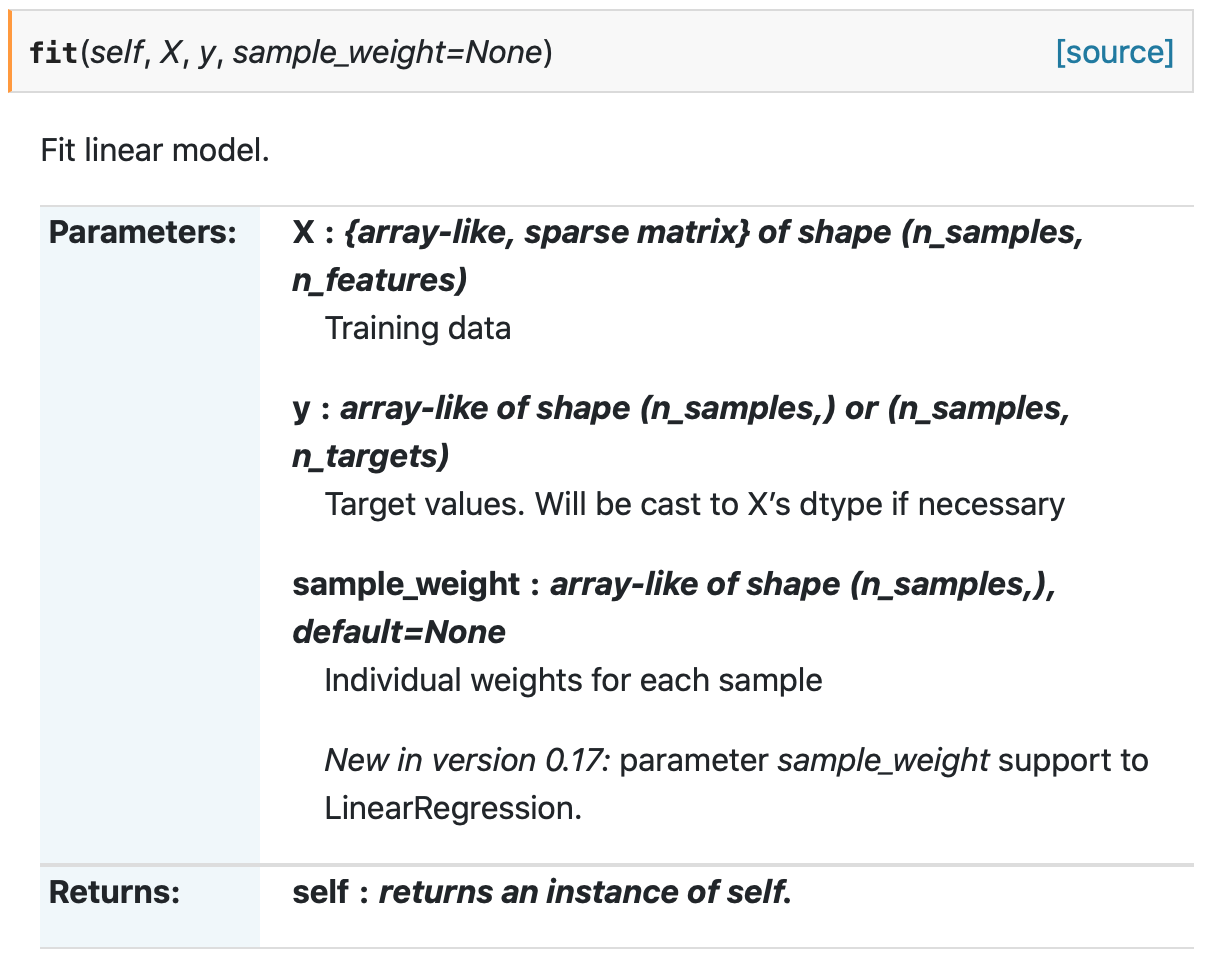
ということで、若干乱暴ではあるが、二次元のArrayを用意する。
X = []
for i in range(1,56):
X.append([i])
いざ
reg = linear_model.LinearRegression()
Y = df['EXP']
# 予測モデルを作成
reg.fit(X, Y)
# 回帰係数
print(reg.coef_)
# 切片
print(reg.intercept_)
# R2(決定係数)
print(reg.score(X, Y))

よしたかは、回帰分析に成功した!
(数式はjupyterのMarkdownで別に書いてます。)
息をするように可視化する。
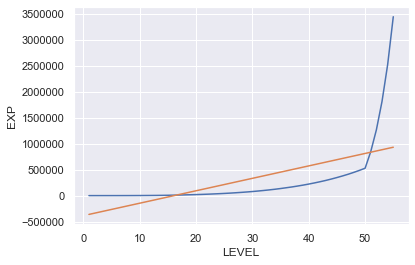
plt.plot(df.index,df['EXP'],label="EXP")
plt.plot(X,reg.predict(X),label="LinearRegression")
plt.xlabel('LEVEL')
plt.ylabel('EXP')
plt.grid(True)
これは全然ダメだ・・・・。確かにR2が0.377なので全く意味をなしていない。
(別に良いんです、これはあくまでも勉強なんです。)
次はあるレベルまでに必要な累積経験値
reg2 = linear_model.LinearRegression()
Y2 = df['CUMSUM_EXP']
# 予測モデルを作成
reg2.fit(X, Y2)
# 回帰係数
print(reg2.coef_)
# 切片 (誤差)
print(reg2.intercept_)
# R2(決定係数)
print(reg2.score(X, Y2))

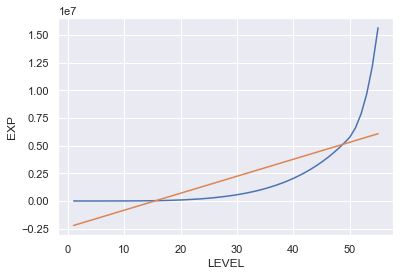
息をするように可視化
こちらも全然ダメだ・・・・。確かにR2が0.575なので、先ほどよりはましとは言え全く意味をなしていない。
(別に良いんです、これはあくまでも勉強なんです。)
多次元化
流石に1次式ではダメなのは明らかなので多次元化してみる
二次元化
まずは説明変数を作る
D1 = []
D2 = []
for i in range(1,56):
D1.append(i)
D2.append(i**2)
df_x = pd.DataFrame({"D1":D1,"D2":D2})
df_x.head()

sklearnのlinear_modelにデータを食わせる
まずは次のレベルまでに必要な経験値
reg3 = linear_model.LinearRegression()
X3 =df_x
Y3 = df['EXP']
# 予測モデルを作成
reg3.fit(X3, Y3)
# 回帰係数
print(reg3.coef_)
# 切片 (誤差)
print(reg3.intercept_)
# R2(決定係数)
print(reg3.score(X3, Y3))

息をするように可視化
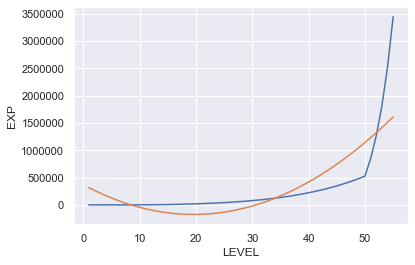
plt.plot(df.index,df['EXP'],label="EXP")
plt.plot(X,reg3.predict(X3),label="LinearRegression")
plt.xlabel('LEVEL')
plt.ylabel('EXP')
plt.grid(True)
R2が0.644っと、さっきよりはマシとはいえ、まだまだFitしているとは言い難い。
次はあるレベルまでに必要な累積経験値
reg4 = linear_model.LinearRegression()
X4 =df_x
Y4 = df['CUMSUM_EXP']
# 予測モデルを作成
reg4.fit(X4, Y4)
# 回帰係数
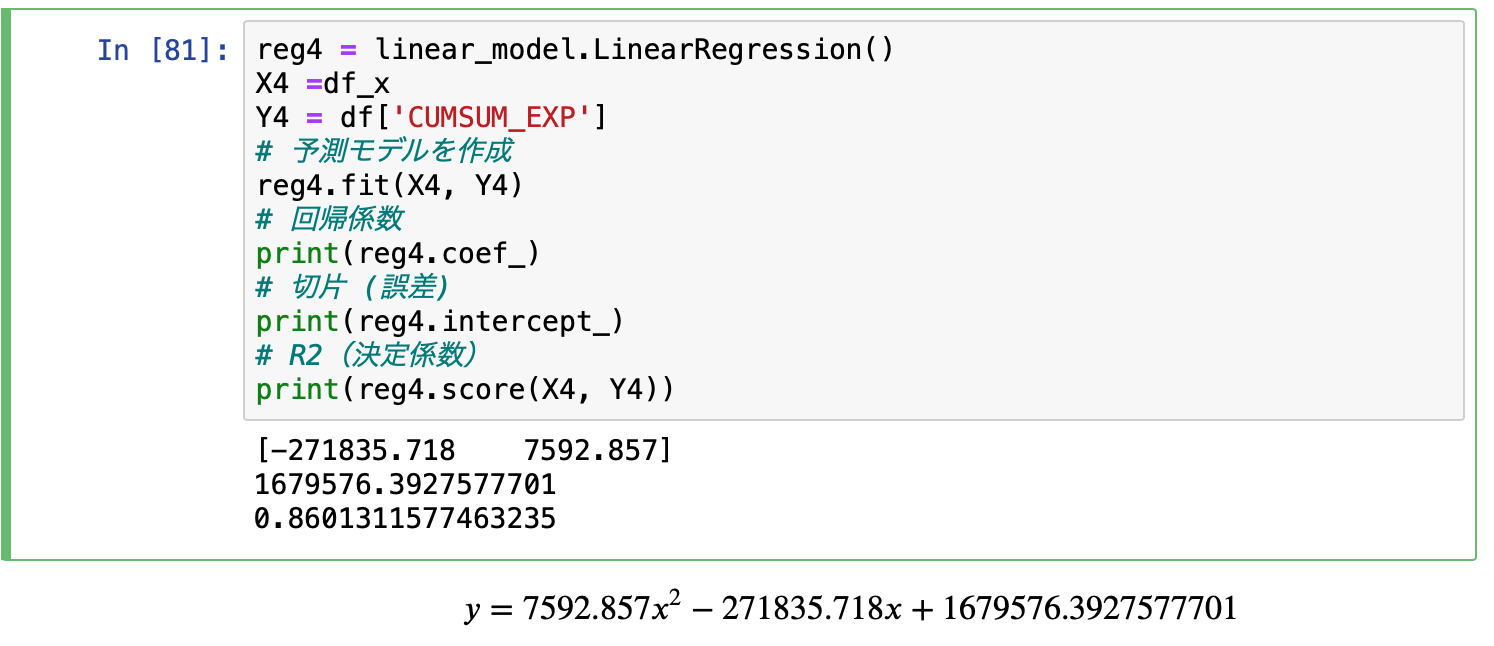
print(reg4.coef_)
# 切片 (誤差)
print(reg4.intercept_)
# R2(決定係数)
print(reg4.score(X4, Y4))
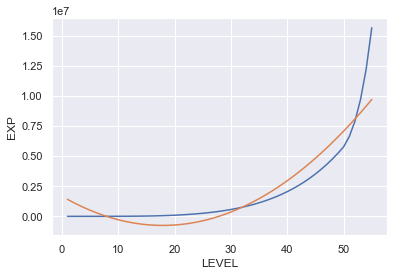
息をするように可視化
plt.plot(df.index,df['CUMSUM_EXP'],label="CUMSUM_EXP")
plt.plot(X,reg4.predict(X4),label="LinearRegression")
plt.xlabel('LEVEL')
plt.ylabel('EXP')
plt.grid(True)
R2が0.860だし、見た目にも結構良いんじゃないでしょうか?
三次元化以降
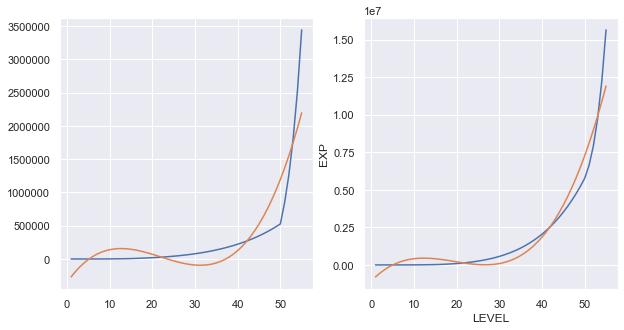
プログラムは同じなので、グラフの結果だけ。
3次元
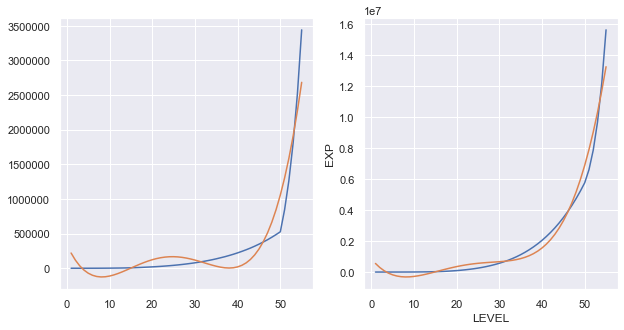
4次元
累積の方はかなりFitしてきました。R2も0.9733まででてます。
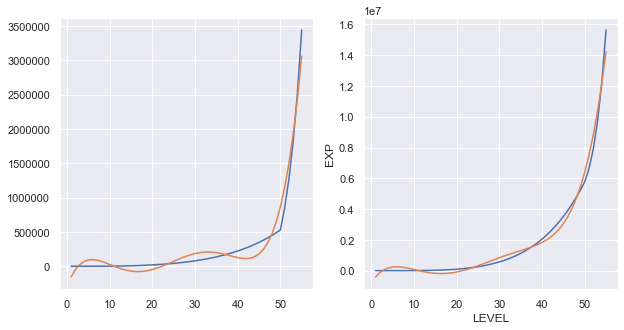
5次元
どちらもほぼFitしたといってもいいのではないでしょうか?
R2は次のレベルまでに必要な経験値が0.961、累積経験値が0.987です。
そして伝説へ
もし、現在の最大レベル55が原作同様に99まで上がるとした場合に必要な累積経験値を試算してみましょう。
これを可視化すると
**レベル99に到達するには1億4千万近い経験値(1,392,549,526)が必要になります。(予想ですよ、予想。)**ちなみにレベル55までに必要な経験値が3,441,626(約350万)なので、404回レベル55にする必要があります・・・・・。
メタルホイミンなら66,311匹、はぐれメタルなら132,623匹、メタルスライムなら904,252匹。もぅ、WWFが動き出しそうな数を乱獲する必要がありまね。
Game Over