はじめに
ロボットアームを動作させようと思った場合にアーム先端の位置や姿勢を指定して動かしたいということが多くあるかと思います。
このような場合、手で直接ロボットアームを動かして、その時の関節角度の値を読み取っておいて、動作させるときに関節角度を指定して動作させる方法(ダイレクトティーチング)や試行錯誤的に関節角度を変化させて動作させるという方法もあります。
しかしこれらは都度試行錯誤を繰り返す必要があったり、正確な位置や姿勢の指定ができなかったり、万能ではありません。
そこで登場するのが逆運動学です。
本記事ではこの逆運動学というものをGNU OctaveとMatlabで動作するプログラム(mファイル)で作ってみたというものになります。
あらかじめ断って起きますと、回転関節のみにより構成されたシリアルリンクアームを対象としています。
運動学
ロボットの(とは限りませんが)位置や姿勢をその時間変化に対応させたりして考える古典力学の一つです。
力学と言っても物理学的な知識を基礎としていないため、重量や力などの概念は出てきません、ひたすら位置や姿勢について考えます。
順運動学と逆運動学
逆運動学があるということは当然その逆の順運動学というものも存在します。
まず順運動学と逆運動学について簡単に触れた上で、実装例を紹介します。
順運動学 (Forward Kinematics)
順運動学はロボットの関節の角度(変位)から手先の位置・姿勢等を求めることを言います。
順運動学の計算式
関節の角度が決まるとその関節に接続された構造部材(リンク)の位置と姿勢は以下のように計算できます。
R_{n+1} = R_{n} r_{n+1} \\
P_{n+1} = r_{n+1} p_{n+1} + P_{n}
ここで、
P_{n} : 根本から数えてN番目のリンクの位置 \\
R_{n} : 根本から数えてN番目のリンクの姿勢 \\
p_{n} : 根本から数えてN番目のリンクのN-1番目のリンクの相対位置 \\
r_{n} : 根本から数えてN番目のリンクのN-1番目のリンクの相対姿勢(関節角度) \\
です。
順運動学の計算は、順方向の計算をひたすら繰り返せば良いので簡単に計算できます.
順運動学の実装
以下のように10行そこそこで実装できます。
ただし、オイラー角から行列を生成する関数(dp_get_rpy_rot)は素のMatlabにはなかったため自前で実装しています。
function [link] = fk(link)
% p0 r0 を計算する
idx = 1;
link(idx).rot = dp_get_rpy_rot(link(idx).dir * link(idx).angle);
link(idx).pos = link(idx).offset;
% すべてのリンクに対して計算する
while link(idx).child > 0
parent = idx;
idx = link(idx).child;
% 順運動学計算
link(idx).rot = dp_get_rpy_rot(link(idx).dir * link(idx).angle);
link(idx).rot = link(parent).rot * link(idx).rot;
link(idx).pos = link(parent).pos + link(idx).rot * link(idx).offset;
end
end
逆運動学
ロボットの手先の位置・姿勢から関節の角度(変位)を求めることを言います。
アルゴリズム
逆運動学の計算式は高次の方程式を解くことになるため、順運動学のように簡単には行きません。
研究者の方々が様々なアルゴリズムを提案しています。
ここでは最急降下法とLM法という2つのアルゴリズムについて実装してみました。
どちらの方法も目標の位置と姿勢に近づくように関節角度を少しずつ変化させていく方式です。
最急降下法では以下のように更新します。
q_{k+1} = q_{k} - E_k / ({g_k}^T g_k) \\
g_k = (J^T W e_k) \\
E_k = ({e_k}^T W_e e_k)/2
LMは以下のような漸化式で関節角度を更新します。
q_{k+1} = q_{k} + H^{−1}_{k} g_{k} \\
H_{k} = J^T_k W_E J_k + W_N \\
W_N = {e_k}^T W_e e_k + \lambda I
ここで
e_k : 残差(目標値と現在値との偏差)
です
アルゴリズムの実装
順運動学に比べると長いですが、
逆運動学も実装してみると20〜30行程度でできます。
ただしここでもクオータニオンの計算などの素のMatlabでは使用できない関数は自前で用意しています。
function link = ik_pseudo_inv()
%% 中略
while E > thr && count < 10000 :
% 基礎ヤコビ行列の計算
jac = jacobian(link, r_idx, offset);
% 目標位置との偏差を求める
cur_pos = positions(link, r_idx, offset);
dpos = pos(1:3) - cur_pos(1:3)';
% 目標姿勢との偏差を求める
axisz = [0,0,1];
a2o_rot = vecs2rot(axisz, offset);
crot = link(r_idx).rot * a2o_rot;
drot = rot * crot';
% 重み付きの誤差を求める
err = [dpos, rot2rpy(drot)]';
gk = jac' * W * err;
E = err' * W * err;
%% 最急降下法更新則の計算
% Eq = 1/2*E;
% Hk = - (Eq)/(gk' * gk);
% dq = - Hk * gk;
%% LM法の更新則の計算
Wn = E* eye(r_idx - 1) + eye(r_idx - 1) * 0.001;
Hk = jac' * W * jac + Wn;
dq = Hk \ gk;
% 角度を更新する
qk = jangles(link, r_idx)';
qk1 = qk + dq;
link = set_jangles(link, qk1);
link = fk(link);
count = count + 1;
end
end
動作確認
GNU Octave & Matlab で確認
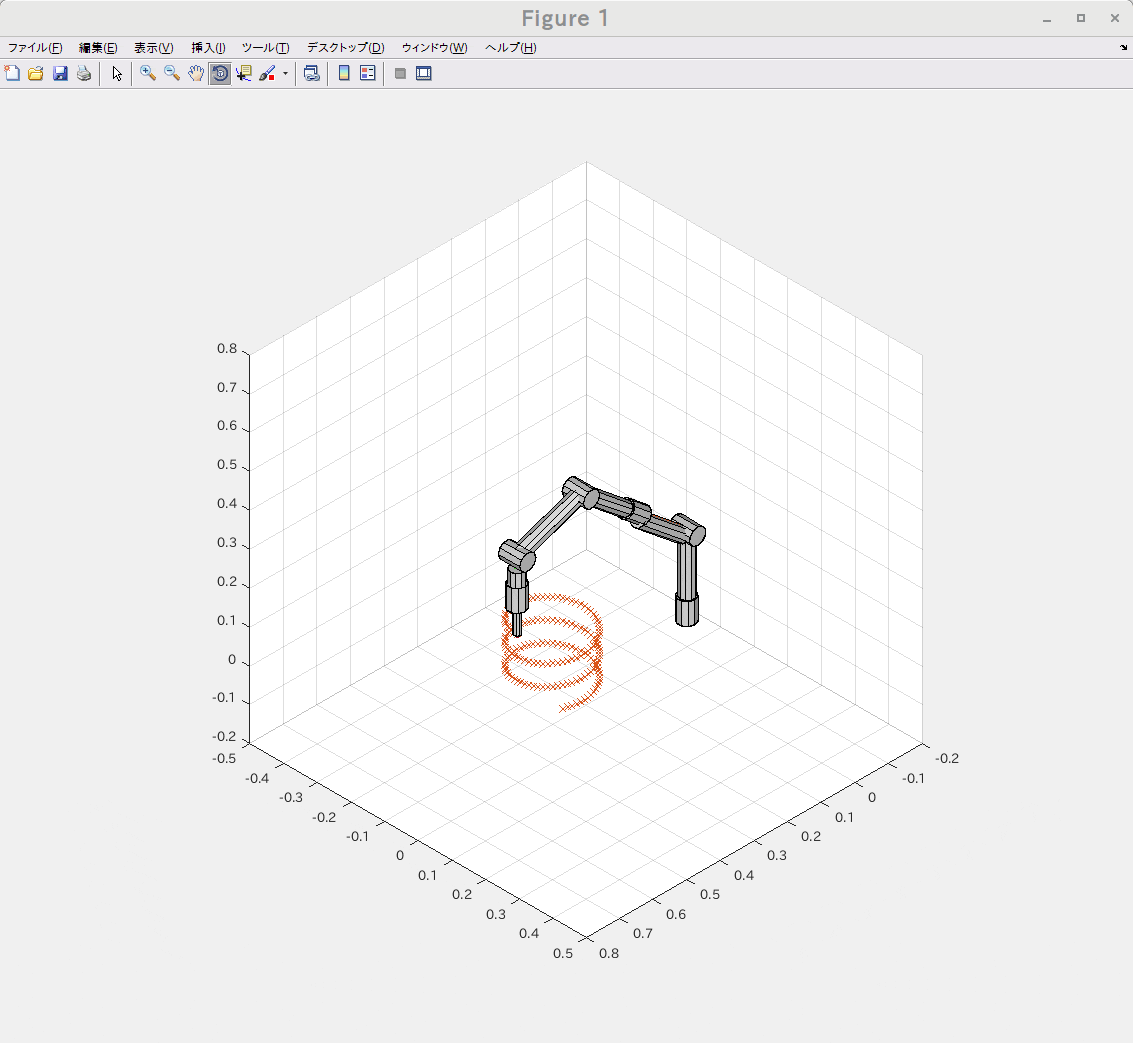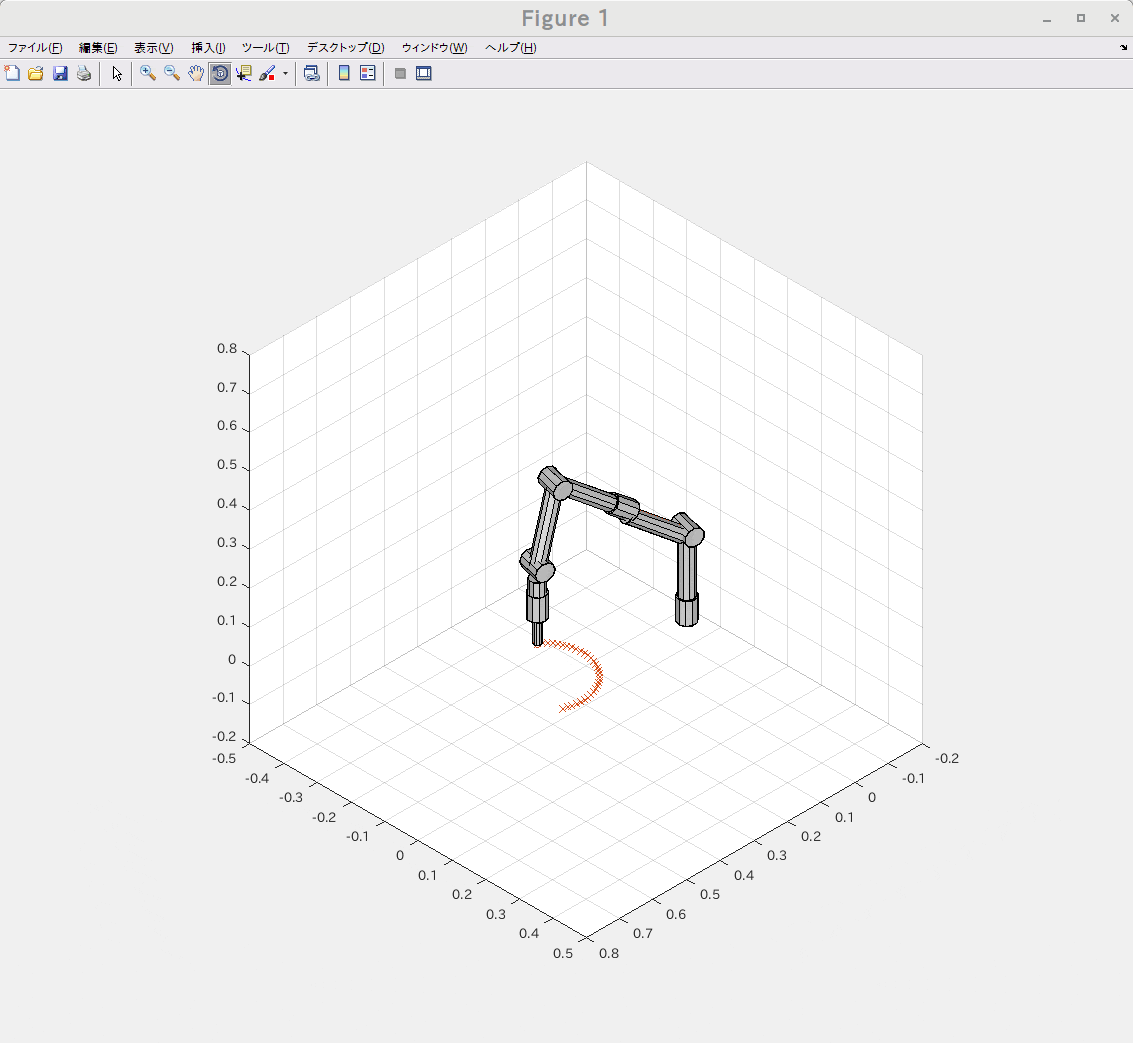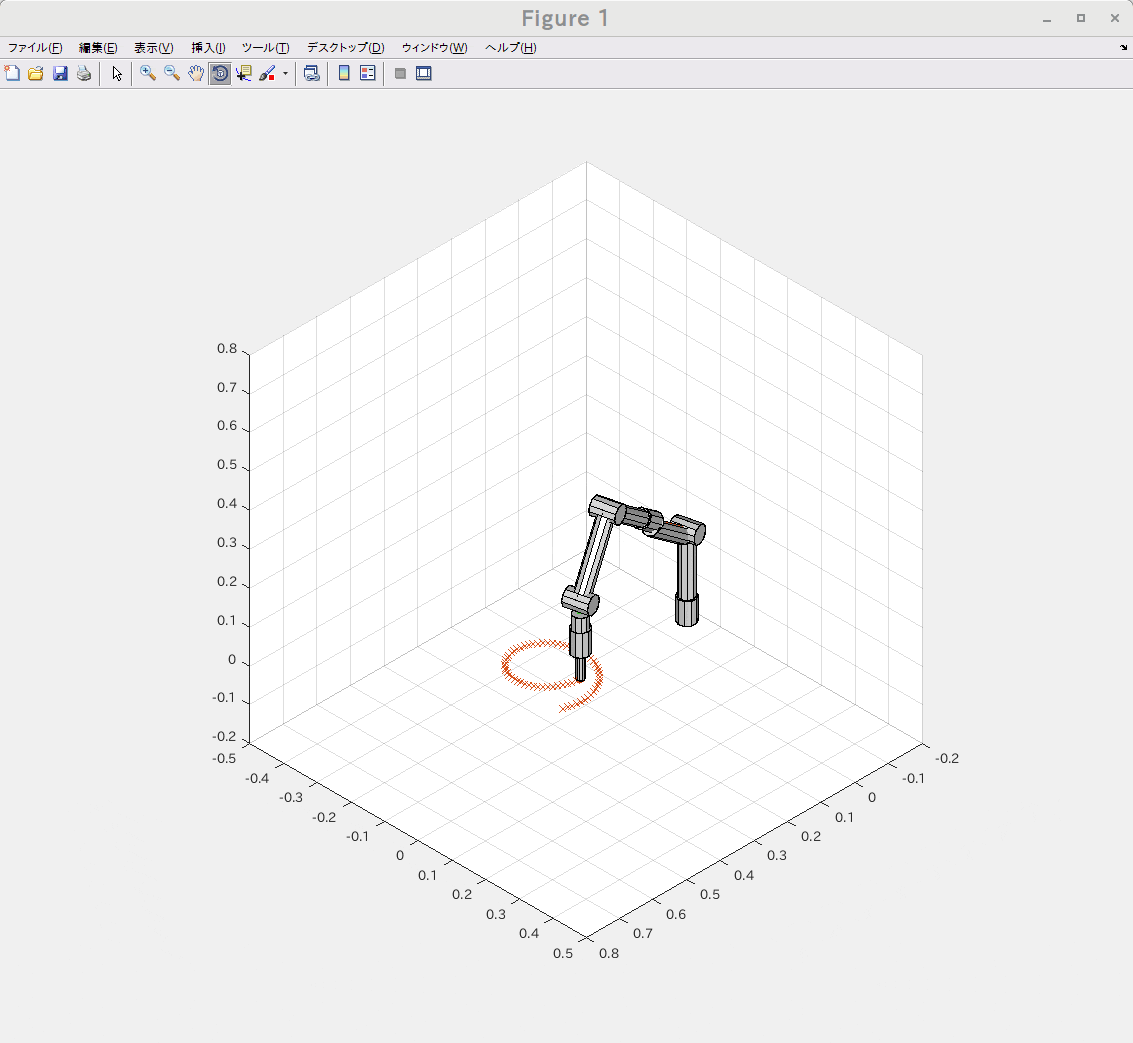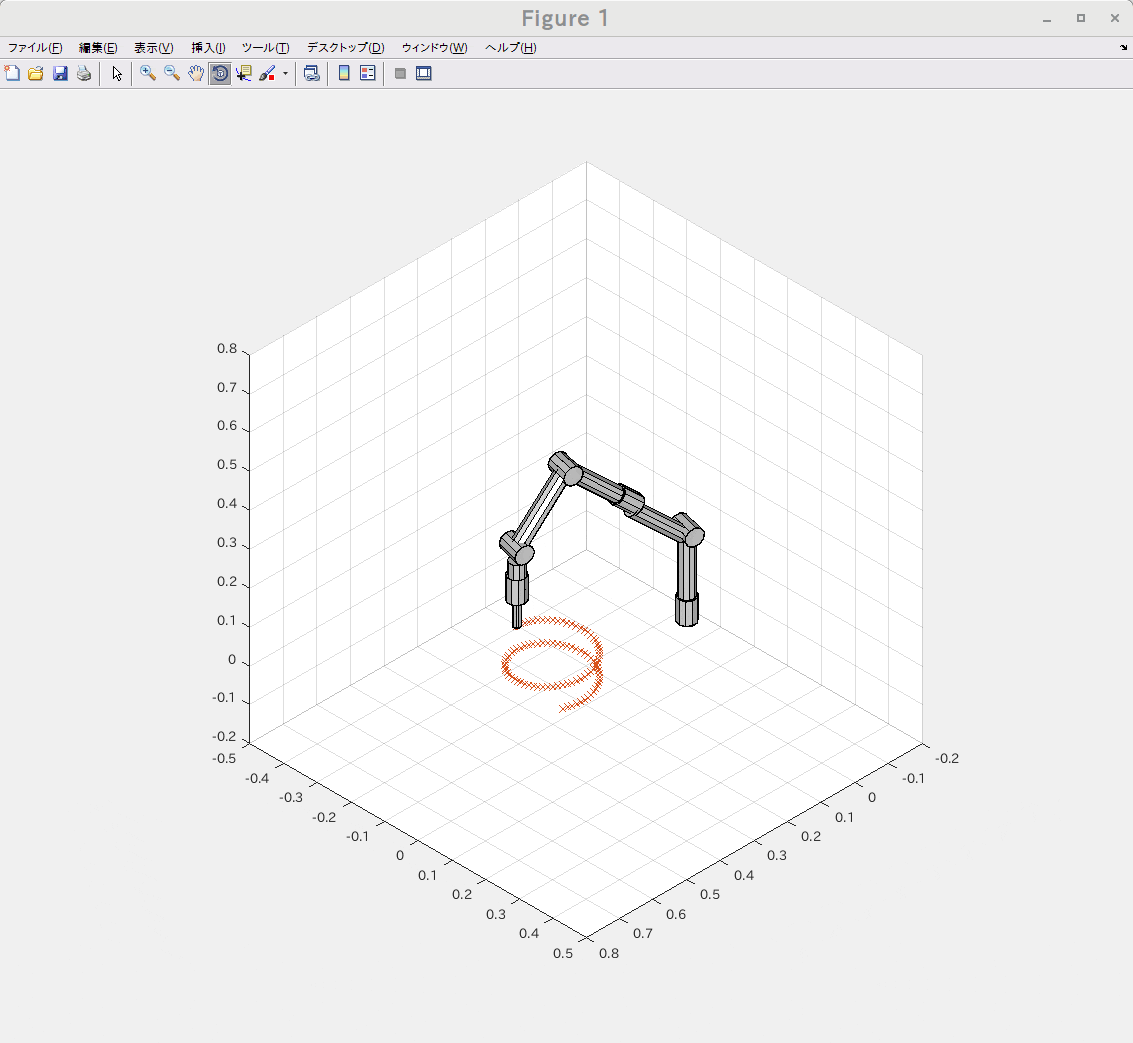
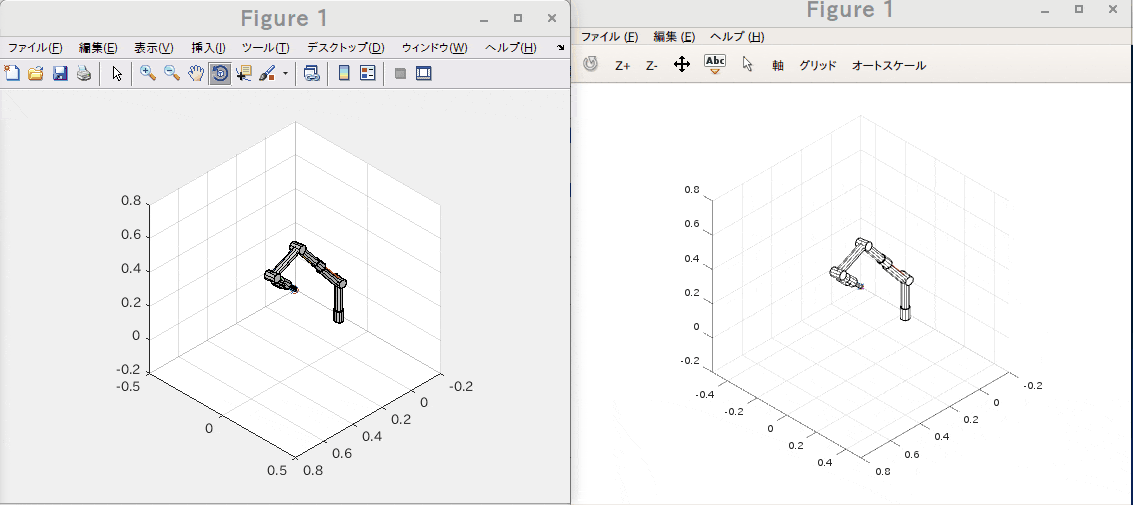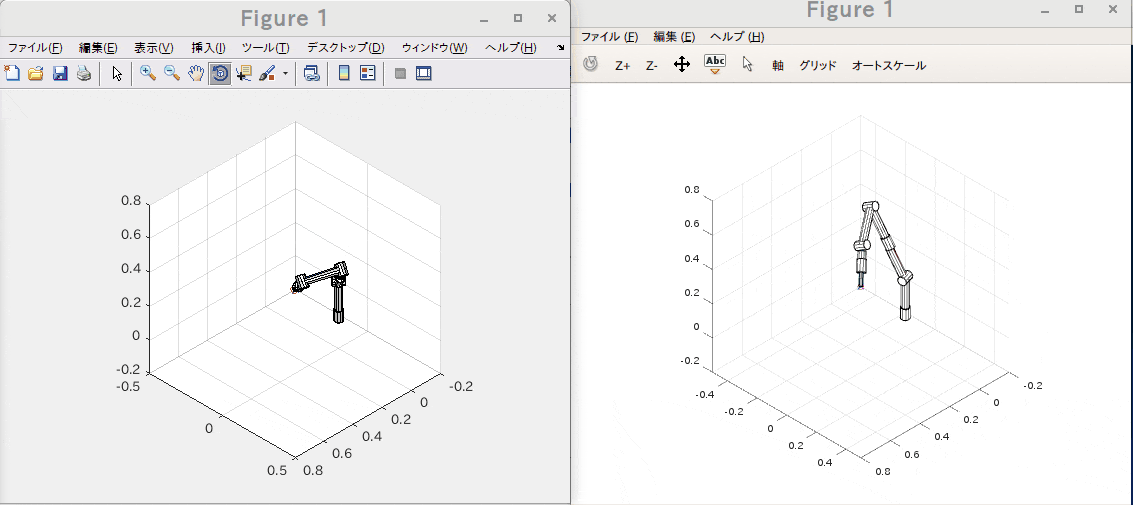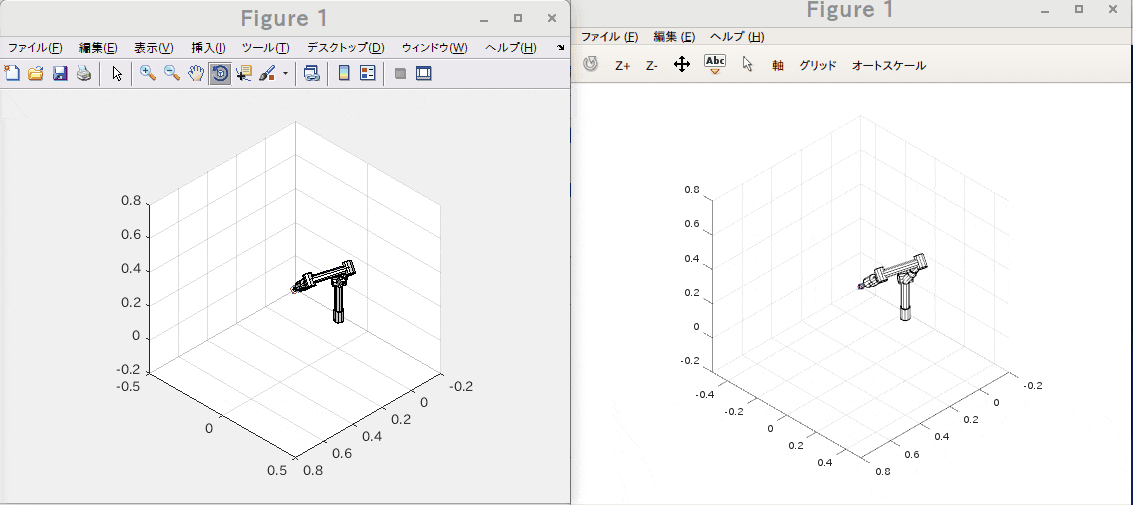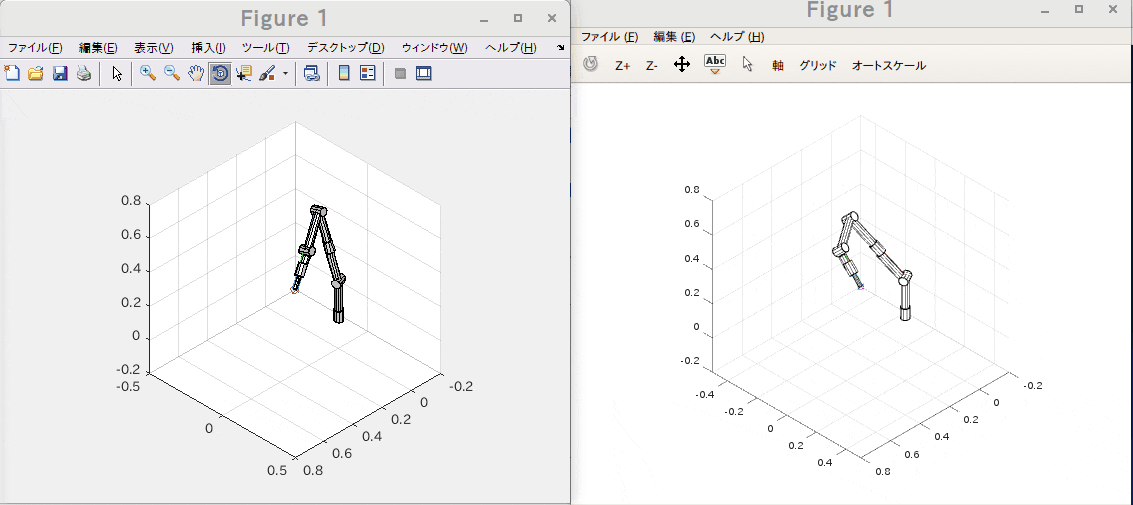
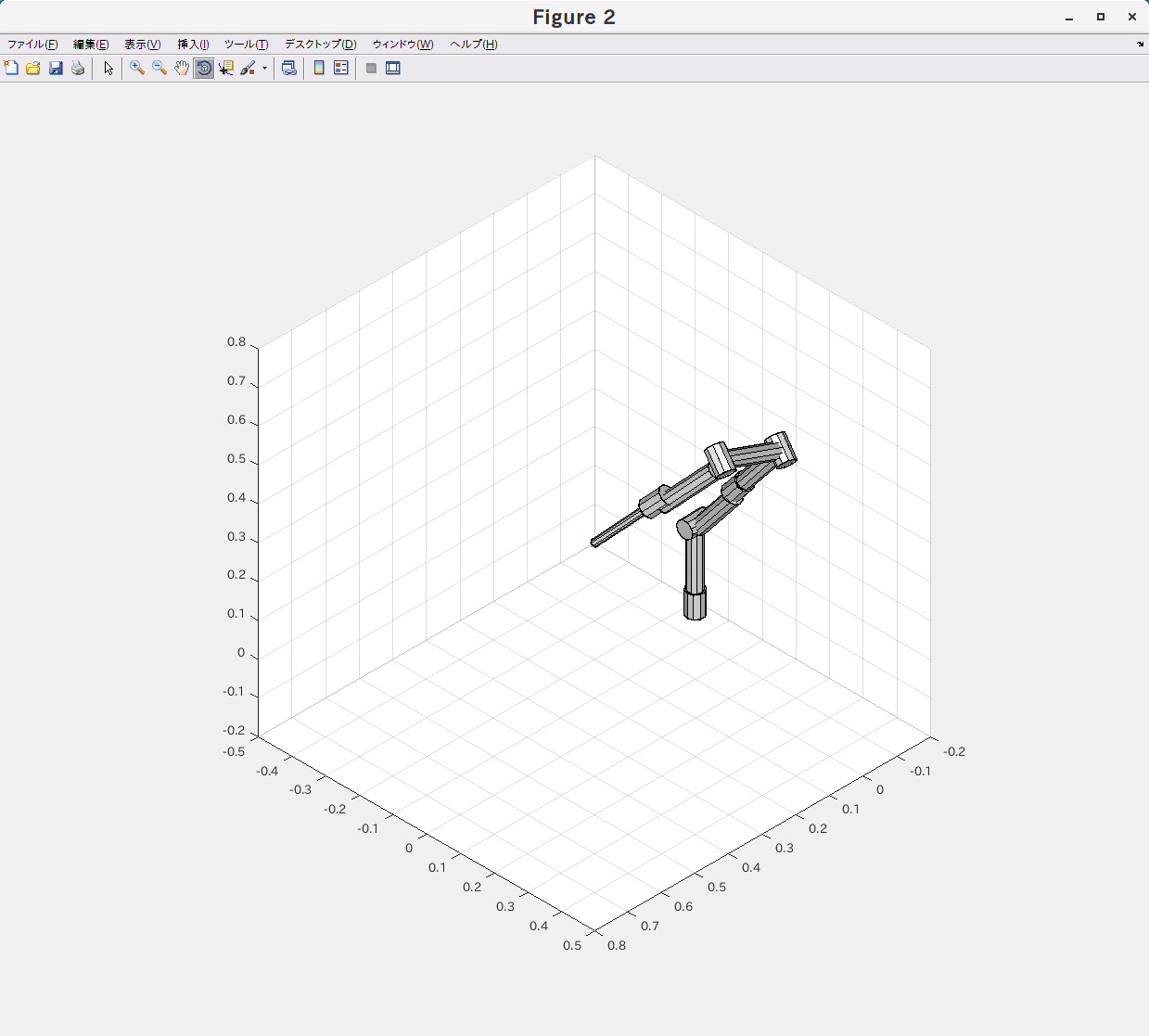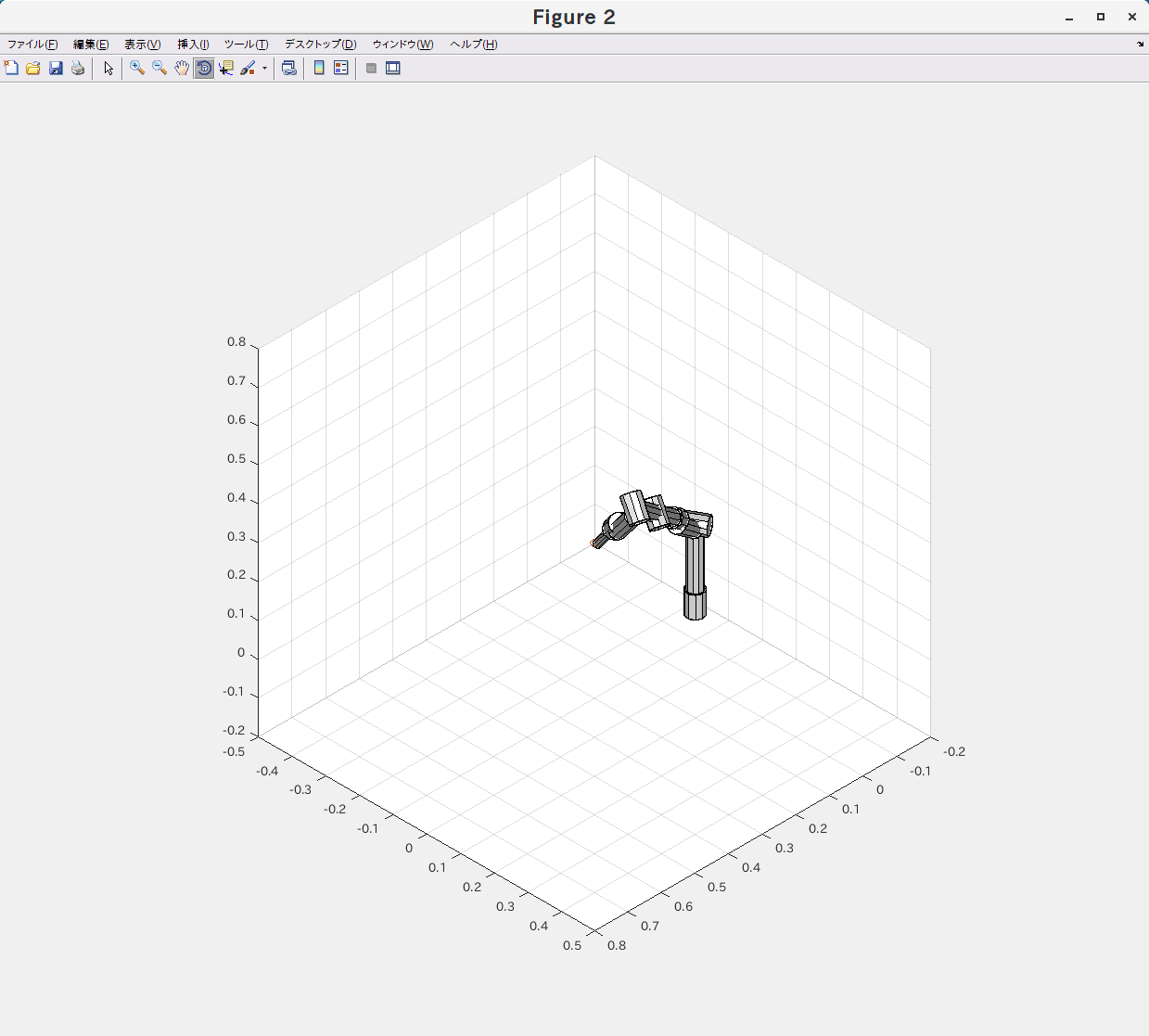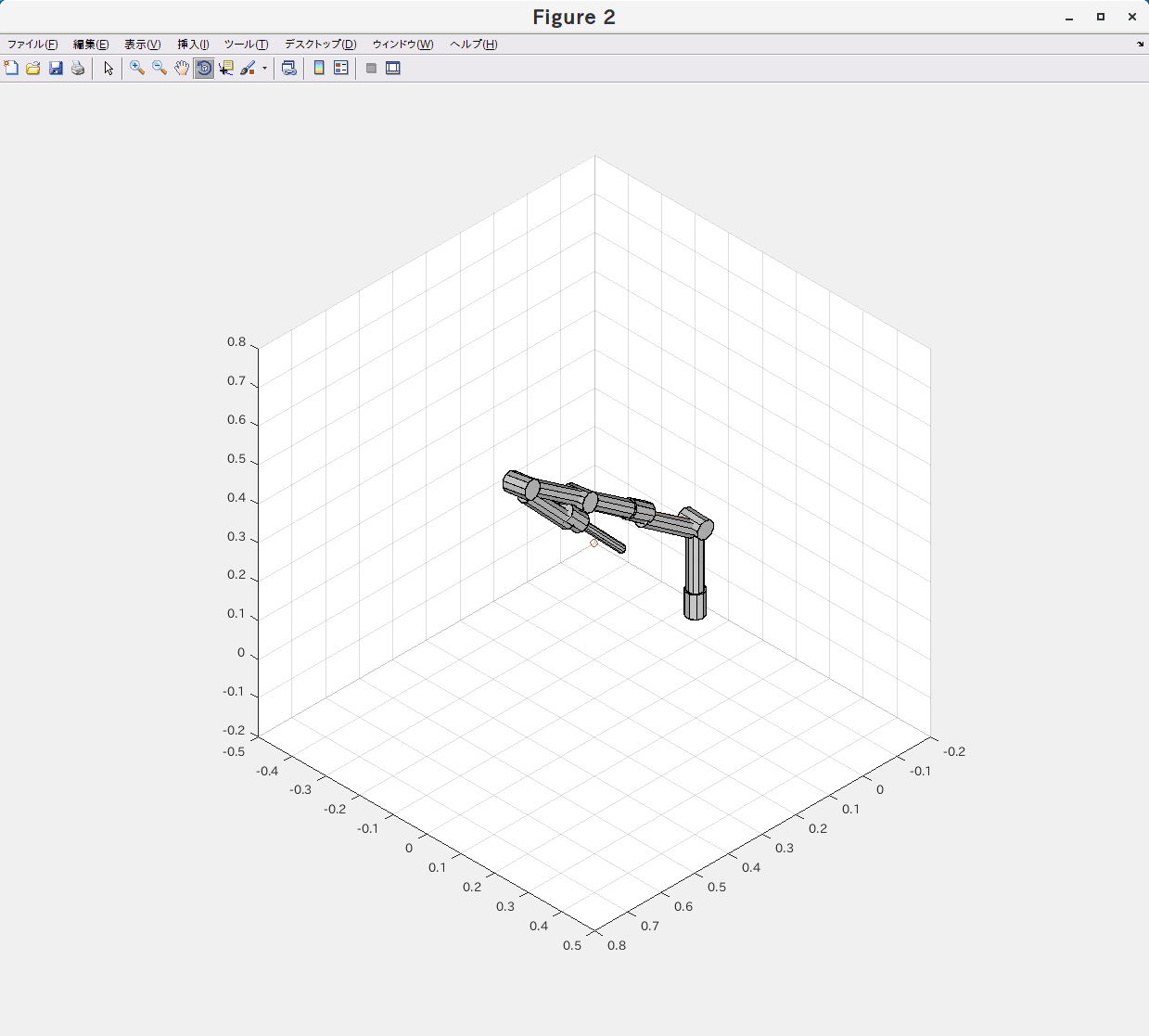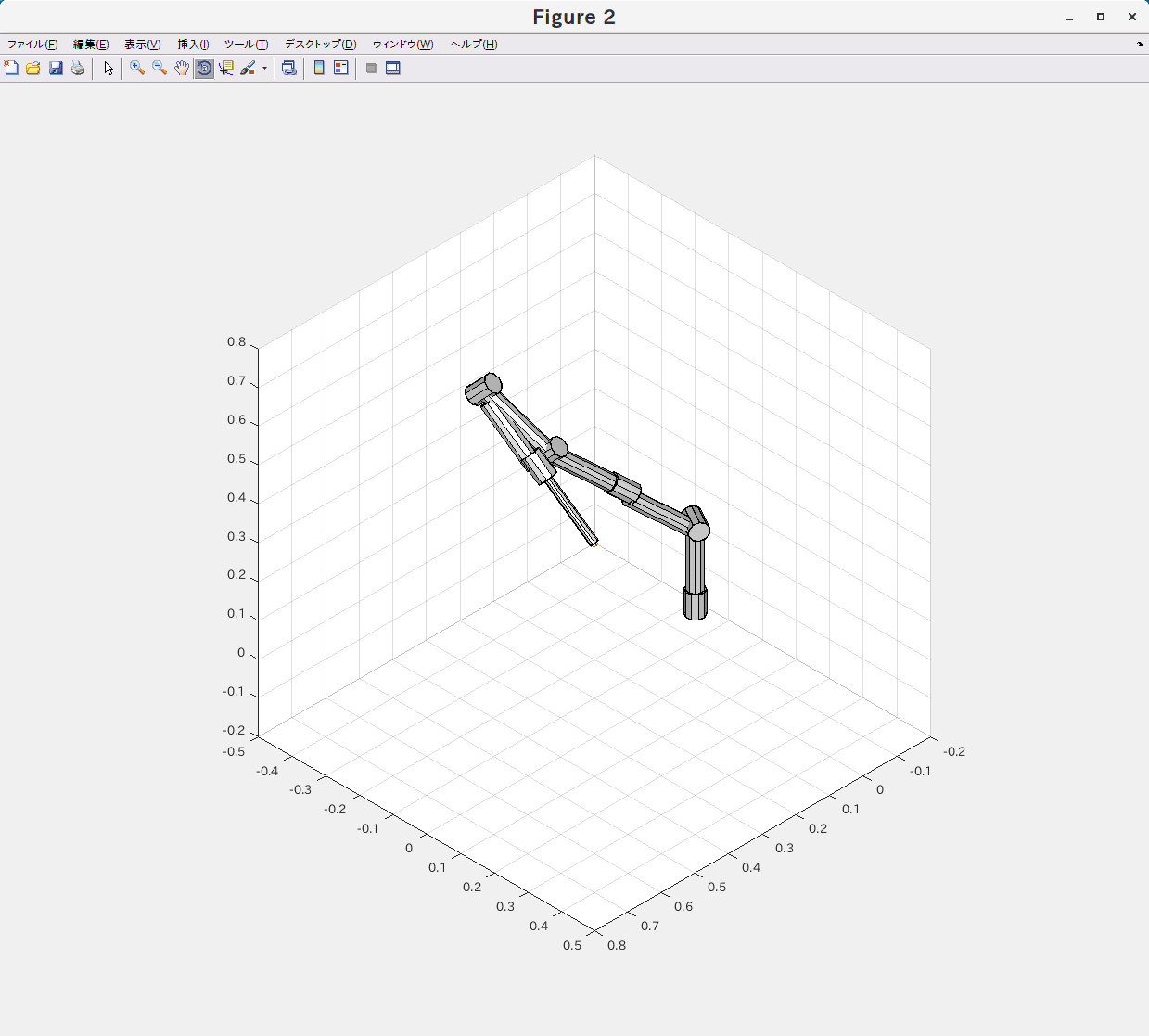
ロボットアームの先端で特定の1点を指しながら姿勢を弧を描くように変化させる様な位置と姿勢の要求を元に逆運動学(IK)をGNU Octave と Matlabの両環境で実行してみました。
左がMatlabで右がGNU Octaveです。
同じスクリプトをほぼ同時に実行開始したのですが、だいぶ速度に差が出ていました。
条件にもよるのでしょうが、今回のケースだと8-20倍程度の差が出ているようでした。
解が存在しないケース
あえて、アームが実現できない目標位置・姿勢を含むような状態になるように先端のリンクの長さを変えて動作確認してみました。
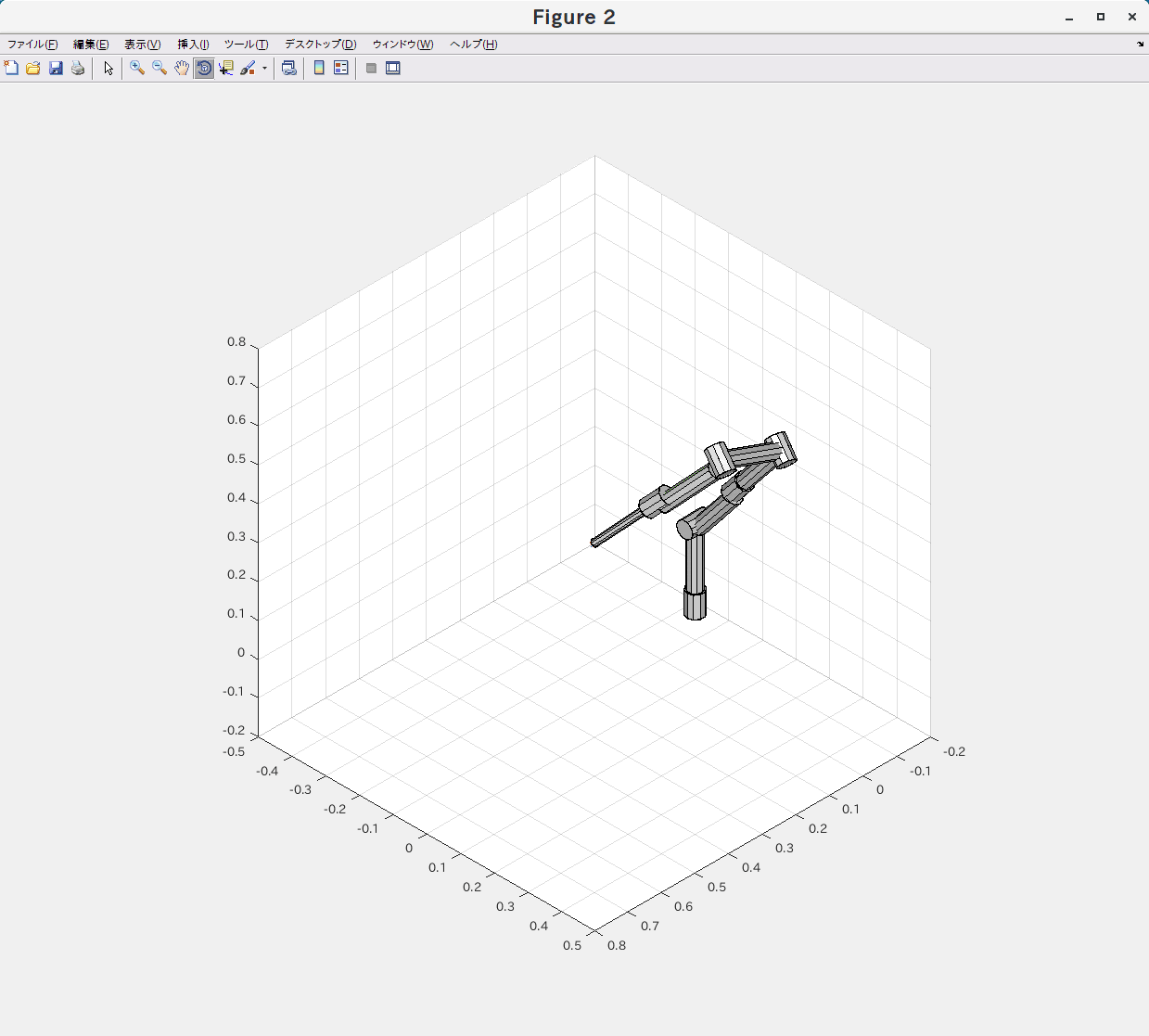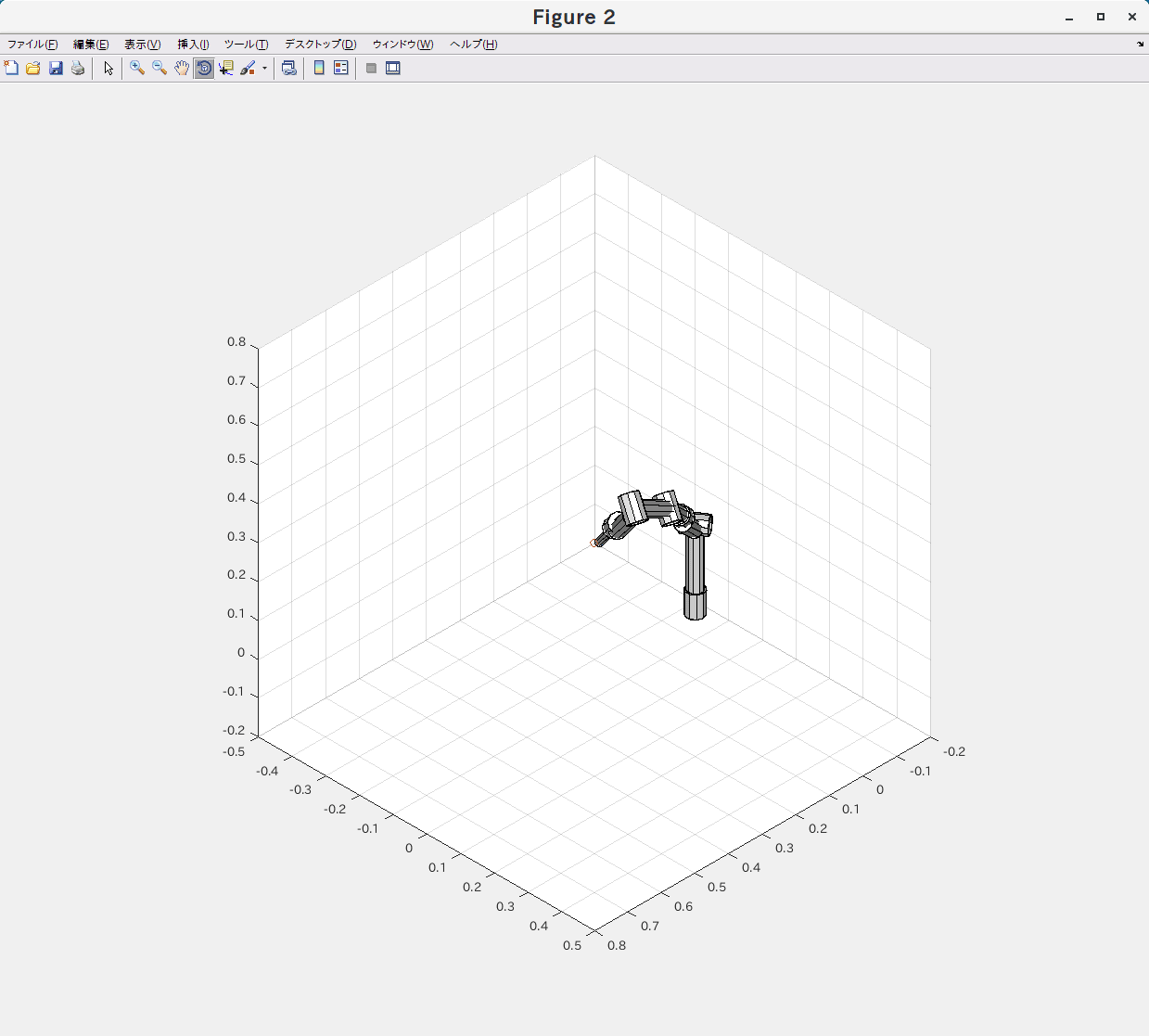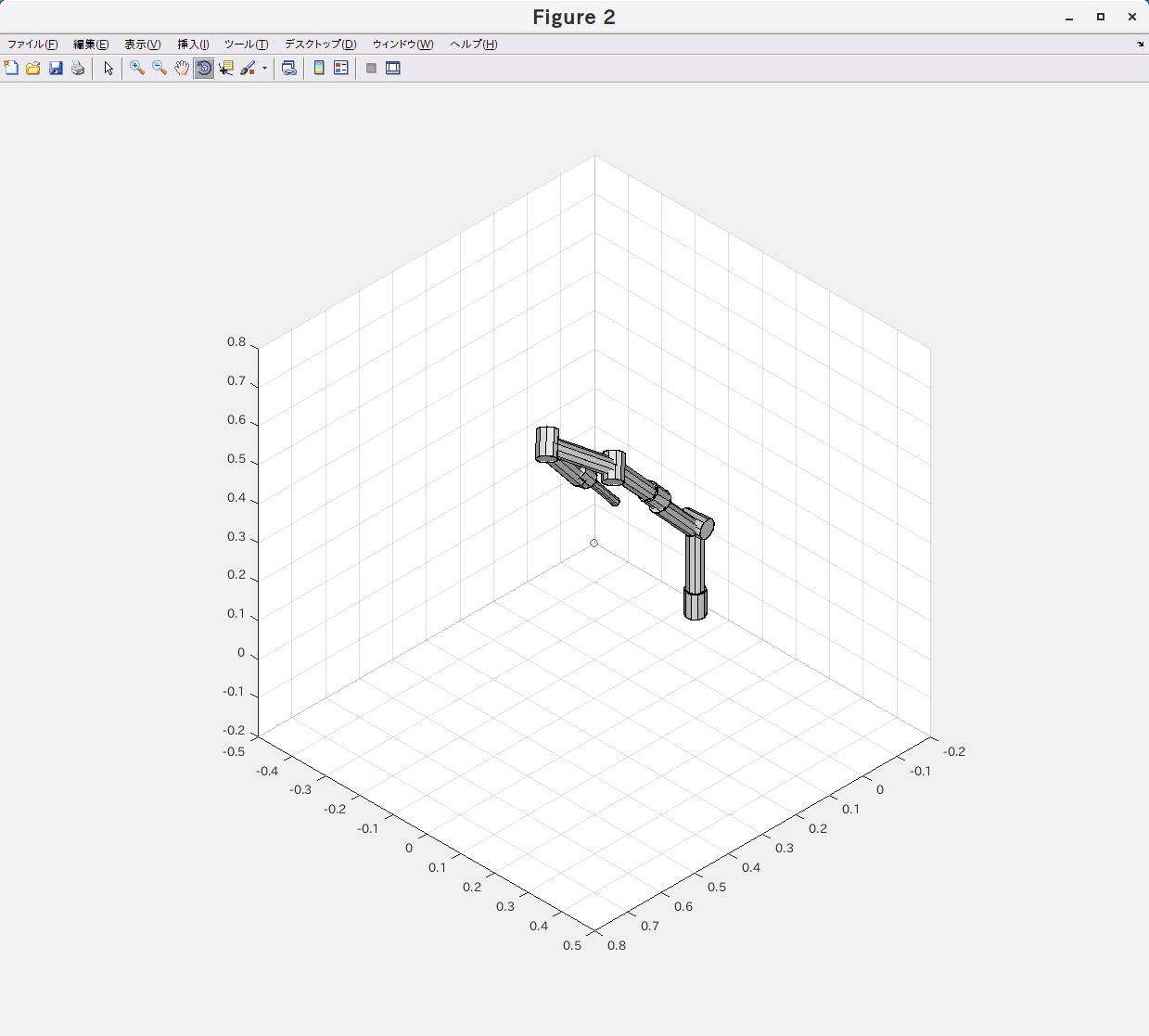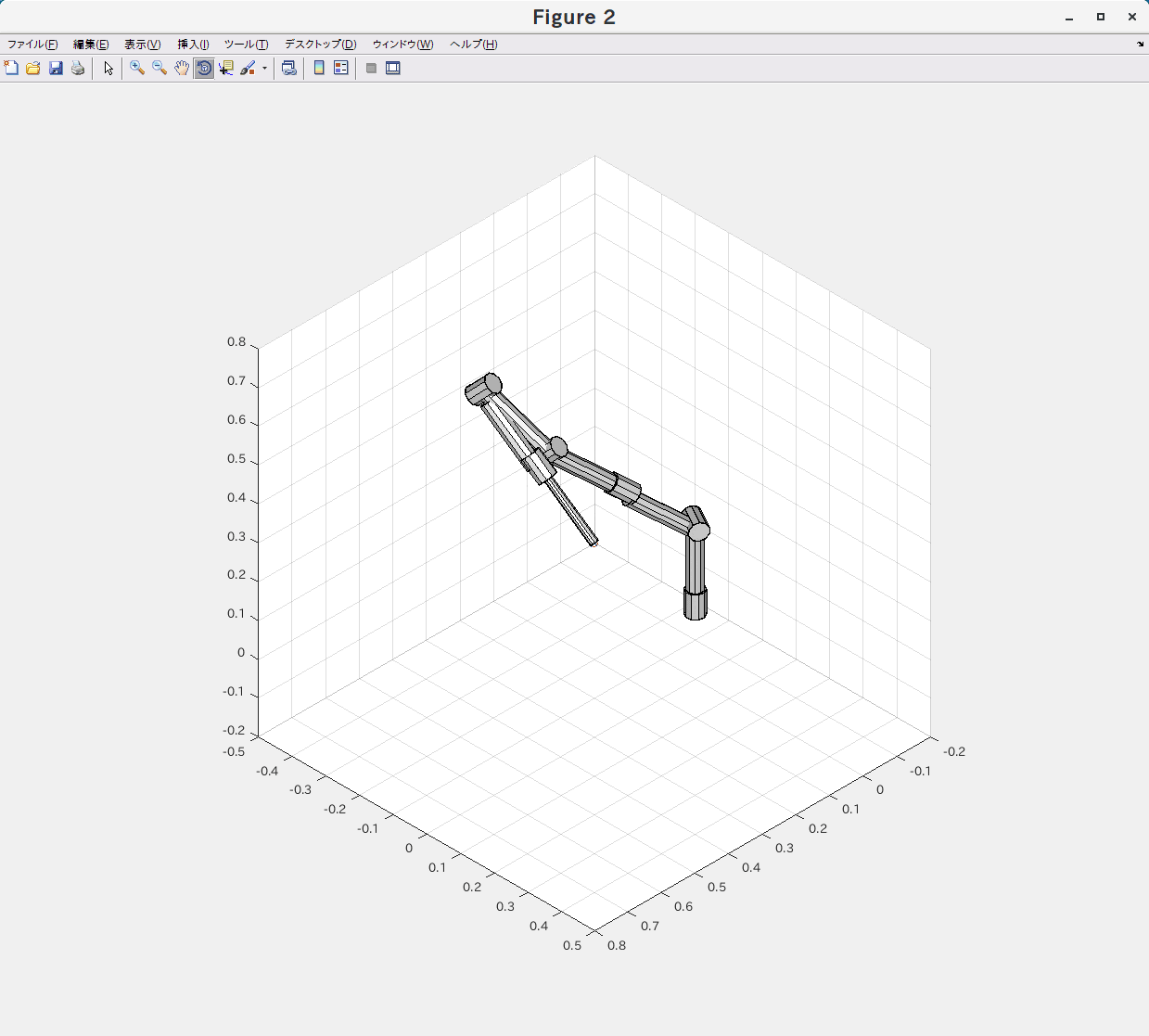
最急降下法
目標が実現できない場合に、アーム全体が暴れるような姿勢の変化が見られます。
実際のロボットにアルゴリズムとして搭載するには注意が必要だと言えます。
LM法
目標が実現できない場合にも、アームが大きく暴れる様なことにはなっていません。
実際には逆運動学の計算を開始し始める際の関節角度の値によっても結果が異なるため一概には言えませんが、逆運動学が解けるかどうかに注意を払わずともそれなりの解が得られそうです。
ソースコードど実行環境
ソースコード
githubにおいてあります.
実行方法
cloneしたプロジェクトのトップに移動してもらい、以下のmファイルを実行してください。
ik_pseudo_inv_test1.m
実行環境
今回の実装では以下の環境で動作を確認しました。
OS依存の機能は使っていないためWindowsでも動くと思います。
- Ubuntu 17.04
- Matlab R2017a
- GNU Octave v4.2.1 (ソースビルド)
また, Ubuntu環境では apt でインストールできる GNU Octave の v4.0.3 では3D描画周りの関数が一部未実装(lightなど)ため実行できません。最新のソースを持ってきてビルドする必要があります。
今後の課題
軽く思いつくだけでも以下の課題があります。
高速化や自己干渉回避などへの対応はMatlab/Octaveのような環境では限界があるかもしれませんが、1.〜3.に関してはなんとかできるかと思います。
特に1. や2. については小規模の変更での対応が見込めるのでやってみると良いかもしれません。
- 冗長自由度を持ったロボットアームへの対応
- 関節の可動範囲制限への対応
- 枝分かれしているロボットへの対応
- 自己干渉回避への対応
- 高速化