乱雑位相近似(RPA)を用いると一様電子ガスにおけるプラズモンのランダウ減衰は
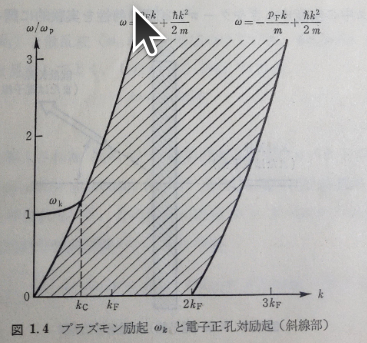
(物理学最前線4共立1983,強結合電子学の多体問題、一丸節夫より)
において、独立電子対励起領域であるkc以上で起こることになる。
RPAにおいてはkc以下ではプラズモンは減衰しない。
重要な点が一つ見過ごされている。RPAできちんとバンド構造を考慮に入れるべき点である。すなわち、バンド構造を考慮に入れると$\chi_0(q=0, \omega \sim プラズモンエネルギー程度)$の虚部がゼロにならないーー>これはフェルミ面と$\omega$をプラズモンエネルギー程度ずらした等エネルギー面が交差を持たざるを得ないからである(証明できる?)。なのでq=0での幅もランダウ減衰が効いている。
ところが一丸(p.57)にはランダウ減衰ではなく電子の衝突効果、とある。

電子の衝突効果の意味がよくわからない(はしご近似で電子正孔散乱を取り込んだ分極関数を計算しなさいという意味ではないかとも思うが、プラズモンのエネルギー運動量保存を考えるとオンシェルにはならないので2体の範囲では虚部が出ない)。4体への崩壊チャネルを計算しないといけないようにも思う。
がいずれにせよ、上述のランダウ減衰を先に計算すべきだと思う。
別記事にしたけどマグノン寿命でも類似のことがある。ただ、q->0 omega->0となる分散なので第一音波のようなことを考えないといけないとかの議論もある。