拡散モデルって何?
拡散モデルでは、$N$次元空間におけるデータ点の集合(解集合)を生成することを考える。確率的に与えることにすると確率分布$p({\bf x})$からベクトル${\bf x} $をサンプリングする問題である。ただし${\bf x} \in R^{\rm N}$.
- 現実的には、$p({\bf x})$もサンプルの集合(以下、解集合とよぶ)$A=${${\bf x}_0,{\bf x}_1,...,{\bf x}_n$}に対して$p({\bf x})=\frac{1}{n}\sum_i\delta({\bf x}-{\bf x}_i)$として与えられている。それゆえ現実的には$A$に類似するものをサンプルする課題であると言える。
- 条件付きサンプリングにも拡張される(たとえば条件指定した絵を書くなど)。
分子動力学的な例題を考える
一定の箱の中に複数の原子を閉じ込めておいて安定解を探す分子動力学的な問題を考える。一定の周期性を仮定するとする。原子間力により原子の並びは規定されるが、いろいろな多形が許されうる状況を考える。たとえばゼオライトのようなものを想定し(Siのみを考える)十分大きい箱を考えておくとその中に整合性をもってきちんと収まる周期的なパターン(結晶)というのは多少のずれを許容するなら多数あり得る。
高温にするとランダム分布になり、アニーリングにより高温でのランダムな構造が、温度ゼロでは、秩序をもつ結晶になるということである。
これを数値的にシミュレーションする。物理学的手法では原子間力を仮定して、力に比例した原子の移動を繰り返すことによりアニーリング。一方、拡散モデルもアニーリング方法の一種であるが、原子間力でなく、温度ゼロでの結晶の多形を表す確率分布$p({\bf x})=\frac{1}{n}\sum_i\delta({\bf x}-{\bf x}_i)$を与えておいて、それに戻るようにアニールしていくことになる。最初に与えたどれかの${\bf x}-{\bf x}_i$にもどるだけでは面白くないが、そこの点を工夫すれば類似のものも生成できる。
拡散モデル、ゼオライト まだあんまりうまくできない
連続的な拡散モデルからの導出
「ランジュバン方程式と拡散方程式の関係,ドリフト電流+拡散電流、拡散とランダムウォーク」をだいたい知ってる人には
「連続的な拡散モデル(拡散方程式)を考えてから逆拡散方程式を考える理論」のほうが、わかりやすい。以下それを説明する。
- まず
dx= f(x,t) dt + g(t) dw \label{eq:1}\tag{1}
のドリフト項(速度場)$f(x,t)$つき拡散のランジュバン方程式から出発する。ここで$dw$は正規化ランダムノイズ、$g(t)=\sqrt{2D(t)}$である。$D(t)$が拡散係数である。$x$はベクトルである。
(1)式と等価な拡散方程式(あるいは、移送方程式、フォッカープランク方程式)は、$dp(x,t) \equiv p(x,t+dt)-p(x,t)$として、
d p = \nabla \left(- p f + D \nabla p \right) dt \label{eq:2}\tag{2}
と書ける。($\ref{eq:2}$)式の拡散方程式は確率(総和が1)のダイナミクスの方程式である。($\ref{eq:1}$)式を解いたランダムモーションを多数回おこなって各時刻で考えると、確率$p({\bf x},t)$の分布となっている。
電流=拡散電流+ドリフト電流、により電子密度の変化が起こる、という式である。
- (2)式を変形して
d p = \nabla \left(- p f + D \nabla p \right) dt\\
= \nabla \left(-p (f - D \nabla\log p ) \right) dt
と書く。ここで$f - D \nabla\log p $をドリフト項であると見たててランジュバン方程式とするなら、拡散項がなくなり、ドリフト項のみの方程式となり、
dx= (f(x,t) - \frac{1}{2} g^2(t) \nabla\log p(x,t))dt \label{eq:3}\tag{3}
となる。
速度場を与える$\nabla \log p(x,t)$はスコア関数と呼ばれる。もしも、これが既知であれば、($\ref{eq:3}$)式は単なる速度場の方程式であり、時間軸を逆にした方程式を考えることができる。これが拡散モデルの考え方である。ランジュバン方程式の立場における、拡散項をドリフト項$\nabla\log p$(速度場)によるものであると考えるのである。
そもそも初期集合が与えられているなら、拡散方程式によって$p(x,t)$は決定されているはずのものであり、$\nabla\log p$は計算可能なものである。拡散はガウシアンノイズを加える過程なので、有限の$t$でもやはりガウシアンノイズを加える過程になる(ガウシアンの畳み込みはガウシアン)。
実際にどうやるのか?は以下。
参考
スコア関数の学習の仕方
$\nabla \log p({\bf x},t)$は損失関数$L=||s_\theta({\bf x},t)-\nabla\log p({\bf x},t)||$(二乗和)を最小化するようにモデル関数${\bf s}_\theta({\bf x},t)$のパラメータ$\theta$を最適化することで機械学習させておく。
これは単純なサンプリング和の最小化手法で可能である.最適化のための損失関数$L$は(以下$t$は固定して考えている)
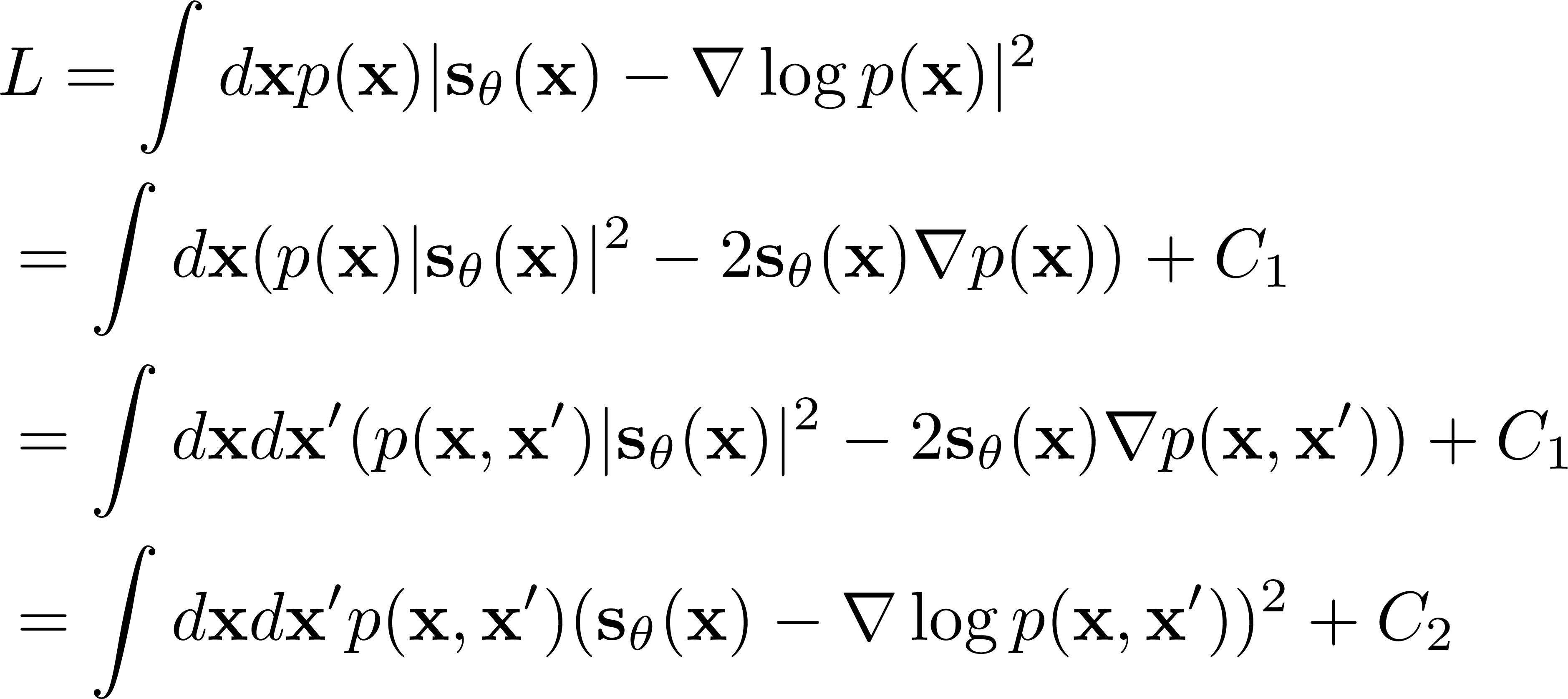
(ここで$C_1,C_2$は$\theta$によらない定数。$p({\bf x},{\bf x}')$は同時確率)
ミソは2つ目の式が$p$の線形項のみである、という点である。なのであえて$p({\bf x},{\bf x}')$という同時確率に置き換えて${\bf x}'$で積分してやるというように変形しても構わない。モデル関数は解析的であり(pytorchに実装されている線形関数、活性化関数などを組み合わせて作る)、$L$の最後の式($C_2$除く)の$p({\bf x},{\bf x})$は以下の簡単な関数である。被積分関数が${\bf x},{\bf x}'$について簡単に定まる関数であるのでサンプリングで評価でき、自動微分による緩和で$\theta$を最適化できる。(参考:岡野原「拡散モデル」p.26(ミソがわかりにくい))
$p({\bf x},{\bf x}')$:
順拡散のときの$p_t({\bf x})$を時刻0での$p_0({\bf x})$の分布(サンプルの分布関数)がガウシアンで拡散していくものであるとするので$p_t({\bf x},{\bf x}')\propto \exp (-|{\bf x}-{\bf x}'|^2/(2\sigma(t)^2) p_0({\bf x}')$を用いる。
ノイズを付加した逆拡散
(2)式を変形して
d p = \nabla \left(- p f + D \nabla p \right) dt\\
= \nabla \left(-p (f - (D+D') \nabla\log p )
\right) dt
- \nabla \left(D' \frac{\partial p}{\partial x}\right) dt
と書くこともできる。これは、時間反転させた時に$D'$という拡散項を導入した標識。ドリフト項を$(D+D')/D$と大きくしておいた分、ノイズを加えてサンプリングすることになる。$\nabla\log p$は特異な点を多く含むだろうから、ある程度なめらかに動かしたいならこういうのもありかと思われる。
モデルのとり方
実際的にはモデルのとり方が問題になる。モデルに局所性がある場合が多い。すなわち近傍構造を見て中心位置を動かす、というようなスコア関数である。このような場合には、最初のサンプル空間でなく、それをも含むもっと大きなサンプル空間へのサンプリングが行われることになる。精度が落ちてしまっていると見ることできるが、多様なものを生成できている、と見ることもできる。
拡散モデルの他の導出法
https://arxiv.org/pdf/2006.11239
が著名論文で拡散モデルをこの導出法にしたがって解説している文献も多い。が、結局は拡散のステップごとに逆拡散ステップを対応させることになり、同様の結論に到達する。離散化したレベルの$L$を考えているので、差分化方程式を導出するときの不定性はない。ただ、離散化したレベルの$L$はいろいろあり得るので方程式もいろいろになる(DDPM,DDIMの違い)。
(学習時の時刻ごとの重みが云々という話もあるがぼくはいまいち理解できてない)
文献
確率フローODE:https://arxiv.org/pdf/2011.13456.pdf
の式(13)(論文https://arxiv.org/pdf/2202.00512.pdfも参照)
がその基礎づけとなる。論文の付録Dに確率フロー方程式の導出があるーGにx依存性がないとして、単純化したバーションを考えるとよい。
それが1式になる。