動機
Python上でCPLEXを使いたいけど英語のマニュアルしかないし、いちいち調べるのも面倒だから自分で日本語のマニュアルを書いてしまえという理由から。
あくまでも自分用なので網羅してるわけではないのでご了承を。
またプログラムについてはjupyter notebookで記述することを想定しています。
以下のサイトをもとにしています。
[公式CPLEX Python API Reference Manual]
https://www.ibm.com/support/knowledgecenter/en/SSSA5P_12.8.0/ilog.odms.cplex.help/refpythoncplex/html/cplex-module.html
参考記事
[PythonでIBMの最適化ソルバ CPLEXを使う]
https://qiita.com/__leopardus__/items/93cac0f97cb22151983a
環境
- MacBook Pro macOS Catalina
- Anaconda
- CPLEX_Studio1210 Academic版
LP(線形計画問題)
今回はLPを解く際に必要なものを中心に記述していきます(jupyter notebook形式)。
以下の問題を例にプログラミングしていきます。
$$
\begin{align}
\max\ \ &2x_1+3x_2 \
\text{s.t.}\ \ &3x_1+2x_2 \leq 24 \
&x_1+2x_2 \leq 16 \
&x_1 \leq 6 \
&x_1 \geq 0,x_2 \geq 0
\end{align}
$$
問題設定
import cplex
まず最適化問題のインスタンスをつくります。
lp = cplex.Cplex()
これで何もデータを持たない空の問題ができました。
次にこの問題がLP(線形計画問題)であることを設定します。
lp.set_problem_type(lp.problem_type.LP)
LP以外の最適化問題にする場合は上記の関数の引数をlp.problem_type.MILPや
lp.problem_type.QPなどにすることで対応させることができます。今回はLPなので
lp.problem_type.LPを代入しています。
次に目的関数について最大化か最小化かを指定します。
デフォルトでは"minimize"つまり最小化問題になっていますが今回は"maximize"最大化に設定します。
lp.objective.set_sense(lp.objective.sense.maximize)
なくてもいいですが問題に名前をつけます。
lp.set_problem_name("test_lp")
ここまででLPについての大枠の設定が完了しました。
変数の設定
次に変数の設定を行います。
lp.variables.add(names=["x1","x2"],lb=[0,0])
変数を新たに加える場合は上記のaddという関数を用いますが、addの引数はobj lb ub types names columnsの6種類があります。それぞれの説明は次のとおりです。
-
obj
目的関数が線形の場合に限るが、目的関数の変数の係数をリストで渡すことができる。
今回の場合はobj=[2,3]のようにすると目的関数を設定できる。 -
lbub
変数の下限(lb)および上限(ub)を指定できる。デフォルトは下限は0上限はNoneとなっている。 -
types
変数のタイプを指定できる。指定の仕方は次のとおり。
- 整数:
lp.variables.type.integerもしくは'I' - バイナリ変数:
lp.variables.type.binaryもしくは'B' - 連続変数:
lp.variables.type.continuousもしくは'C' - 半整数:
lp.variables.type.semi_integerもしくは'N' - 半連続:
lp.variables.type.semi_continuousもしくは'S'
ただしtypesを指定すると、すべての変数を連続に指定しても問題の型がMIPになるので注意
-
names
変数の名前を指定できる。 -
columns
制約式を設定できるらしいが複雑そうなので省略。
目的関数・制約式の記述
目的関数を設定します。
lp.objective.set_linear("x1",2)
lp.objective.set_linear("x2",3)
もしくは
lp.objective.set_linear([(0,2),(1,3)])
上記のように引数は(変数名,係数)か(変数番号,係数)で与え、変数ごとに個別に設定してもまとめて設定しても良いです。
次に制約式の記述をします。
lp.linear_constraints.add(names=["C1","C2","C3"],
lin_expr=[cplex.SparsePair(ind=["x1","x2"],val=[3,2]),
cplex.SparsePair(ind=["x1","x2"],val=[1,2]),
cplex.SparsePair(ind=["x1","x2"],val=[1,0])],
senses=["L","L","L"],
rhs=[24,16,6])
もしくは
lp.linear_constraints.add(names=["C1","C2","C3"],
lin_expr=[[["x1","x2"],[3,2]],
[["x1","x2"],[1,2]],
[["x1","x2"],[1,0]]],
senses=["L","L","L"],
rhs=[24,16,6])
線形の制約を追加する場合はlinear_constraints.addという関数を用いる必要がありますが、これも変数同様複数の引数が設定されています。
-
names
制約式の名前を設定できる。 -
lin_expr
制約式の左辺の部分を指定する。形はSparsePairか行列形式のリストを与える。 -
rhs
制約式の右辺の部分を指定する。 -
senses
制約式の左辺と右辺の関係を表す等号あるいは不等号を指定する。
記号と指定すべき文字の対応は以下のとおり。
- $\leq$:
'L' - $\geq$:
'G' - $=$:
'E' - 範囲制約:
'R'
-
range_values
範囲制約の値を指定できる。
求解
問題の定義ができたのでいよいよ求解しますが、その前にこれまで定義してきた問題を出力してみます。
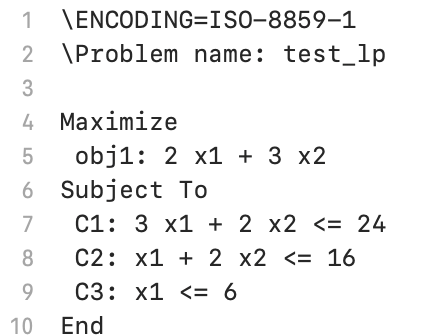
lp.write("test.lp")
出力したファイルを見ると正しく問題が定義できています。
正しく定義できたところで解を求めます。
lp.solve()
最適化の結果、最適解が得られたかどうかを表示します。
print(lp.solution.get_status_string())
出力:optimal
となり、最適解が得られています。
最適解と最適値を表示します。
print(lp.solution.get_values())
print(lp.solution.get_objective_value())
出力:
[4.0, 6.0] 26.0
となって正しく解が得られました。
次回
次回があるか分かりませんがQPを取り扱いたいと思います。
コード
import cplex
lp = cplex.Cplex()
lp.set_problem_type(lp.problem_type.LP)
lp.objective.set_sense(lp.objective.sense.maximize)
lp.set_problem_name("test_lp")
lp.variables.add(names=["x1","x2"],lb=[0.0,0.0])
lp.objective.set_linear([("x1",2),("x2",3)])
lp.linear_constraints.add(names=["C1","C2","C3"],
lin_expr=[[["x1","x2"],[3,2]],
[["x1","x2"],[1,2]],
[["x1","x2"],[1,0]]],
senses=["L","L","L"],
rhs=[24,16,6])
lp.write("test.lp")
lp.solve()
print(lp.solution.get_status_string())
print(lp.solution.get_values())
print(lp.solution.get_objective_value())