この記事は CSS Advent Calendar 2019 10日目の記事です。
はじめに
僕はCSSが大好きで、普段からCSSテクニックやCSSハックなどを探しまくっています。最近ではFirefox69のみに適用されるCSSハックを見つけたりしました。
// Firefox69
@supports selector(_>_) and (not (text-underline-offset: 0)) {
_:-moz-is-html, .selector {
property: value;
}
}
@supports クエリが実装されたため、CSSハックも探すのが昔と比べてかなり楽になっています。こんな感じでCSSの仕様やバグをついたテクニックを探すのが特に好きです。
さて、今回は実務でも使って欲しいレスポンシブ対応が楽になるテクニックの紹介です。レスポンシブ対応といえば、メディアクエリを使ってブラウザ幅ごとに制御する方法が一般的です。それに対し、毎年登場するデバイスのブラウザ幅は多種多様で今後も増え続けると思われます。そのため、タブレットなら 768px 以上、PCなら 992px 以上と決めて実装していると、あるブラウザ幅でデザインが崩れている...なんてことになりかねません。
では、メディアクエリを細分化してどのブラウザ幅になっても問題ないようにすれば良いかというと、そうではありません。
body {
font-size: 15px;
}
@media (min-width: 320px) {
body {
font-size: 16px;
}
}
@media (min-width: 336px) {
body {
font-size: 17px;
}
}
@media (min-width: 352px) {
body {
font-size: 18px;
}
}
...
これは少し極端な例ですが、あらゆるブラウザ幅に対応するのは無理があります。そこで、便利なのが calc() 関数と vw 単位です。
calc()関数とvw単位
calc() 関数は calc(100% - 100px) のように異なる単位どうしで計算ができます。演算子との間にはスペースを空けておきます。vw 単位はブラウザ幅を表しており、100vw がブラウザ幅いっぱいとなります。ブラウザ幅が変化すれば、100vw のときの px 値も変化します。50vw とすれば常にブラウザ幅の半分の値となります。ただし、vw 単位はブラウザのスクロールバーの幅を含むことに注意が必要です。
1次関数
ブラウザ幅によって変動する vw 単位があれば、メディアクエリを細分化することなく値を設定できます。しかし、そのまま vw 単位を使おうとするとこのブラウザ幅のときにはこの値になって欲しいといったようなことが難しいと分かります。そこで、calc() 関数を使って1次関数にしてしまえば、直感的に指定できるようになります。
まずは、1次関数の定義からです。1次関数は2点の座標 $ (x_1,\ y_1),\ (x_2,\ y_2) $ を通る直線なので、
y = ax + b \quad \left( a = \cfrac{y_2-y_1}{x_2-x_1},\ \ b = y_1 - ax_1 \right)
と定義されます。ここではブラウザ幅 320px のときは font-size: 20px、ブラウザ幅 768px のときは font-size: 40px となるように2点 $ (320,,20),\ (768,,40) $ をとります。2点が決まったので、$ a,\ b $ の値を求めます。
\begin{align}
a &= \cfrac{40 - 20}{768 - 320} = \cfrac{20}{448} = \cfrac{5}{112}\\
b &= 20 - \cfrac{5}{112} \times 320 = \cfrac{2240 - 1600}{112} = \cfrac{640}{112} = \cfrac{40}{7}
\end{align}
よって、1次関数の式は以下のようになります。
y = \cfrac{5}{112}x + \cfrac{40}{7}
ここで、$ x $ はブラウザ幅を表しているので $ 100,\mathrm{vw} $ と置き換えられます。
y = \cfrac{5}{112} \times 100\,\mathrm{vw} + \cfrac{40}{7}
これで、1次関数の式が求められたので calc() 関数とメディアクエリを使って表現します。

// ブラウザ幅 < 320px
body {
font-size: 20px;
}
// 320px ≦ ブラウザ幅 < 768px
@media (min-width: 320px) {
body {
font-size: calc((5 / 112) * 100vw + (40 / 7) * 1px);
}
}
// 768px ≦ ブラウザ幅
@media (min-width: 768px) {
body {
font-size: 40px;
}
}
320px 以上 768px 未満の間だけ1次関数にして、両端の区間はそれぞれ最小値と最大値が一定になるようにしています。
body {
font-size: 1.25em;
}
@media (min-width: 20em) {
body {
font-size: calc((5 / 112) * 100vw + (40 / 7 / 16) * 1em);
}
}
@media (min-width: 48em) {
body {
font-size: 2.5em;
}
}
分かりやすいように px で表記しましたが、できればアクセシビリティを考慮して em や rem などの相対値を使うと良いです。また、メディアクエリ部分は px 表記なのに、font-size を em で指定するなど、絶対値と相対値の組み合わせは絶対にしてはいけません。
2次関数
1次関数が使えるだけでも非常に便利ですが、2次関数で曲線が使えるともっと便利だなと思いました。2次関数の一般形は、
y = ax^2 + bx + c
で表されますが、現在のCSSでは $ x^2 $ という部分を表現できません。calc() 関数の仕様によると乗算の場合、引数の少なくとも1つがNumber型である必要があります。つまり、$ x^2 $ を表す calc(100vw * 100vw) は両方とも単位付きであるため不正な値となります。仕様上不可能ということが分かったので、1次関数による線形補間で近似することにします。
近似するために、まずは2次関数を求めます。2次関数にはIllustratorなどのベクターソフトでも使われているベジェ曲線を用います。ベジェ曲線は $ 1,\ 2,\ 3,\ ...,\ n $ 次とありますが、ここでは2次ベジェ曲線を使います。2次ベジェ曲線は始点と終点、そして制御点の3点からなる曲線です。始点と終点は1次関数のときの2点をそのまま使い、制御点は $ (660,,22) $ とします。制御点を変えることで曲線の曲がり具合を調整できます。
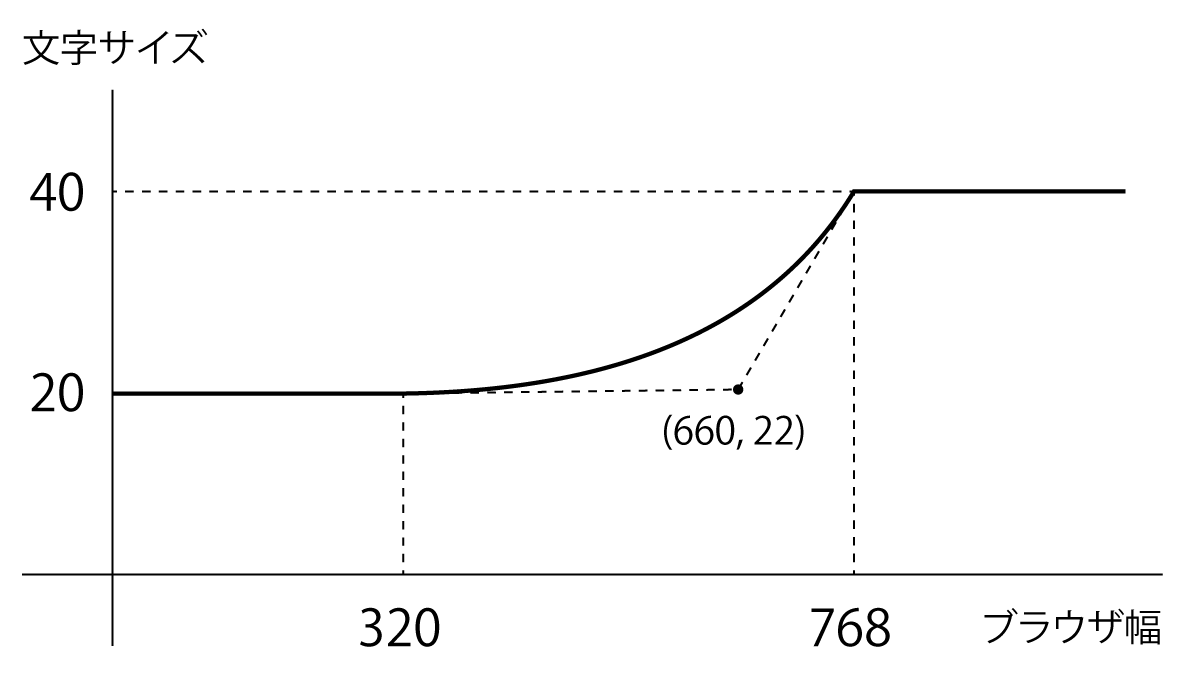
ベジェ曲線の定義より、制御点を $ B_1,\ B_2,\ ...,\ B_{N-1} $ とすると2次ベジェ曲線は、
\begin{align}
P(t) &= \sum_{i=0}^{N-1} B_i\,J_{N-1,i}\,(t)\\
&= \sum_{i=0}^{2} B_i\,J_{2,i}\,(t)\\
&= B_0J_{2,0}(t) + B_1J_{2,1}(t) + B_2J_{2,2}(t)
\end{align}
ここで、$ J_{n,i},(t) $ はバーンスタイン基底関数より、
J_{n,i}\,(t) =
\left(\begin{matrix}
n \\
i
\end{matrix}\right)
t^i (1-t)^{n-i}
よって、求める2次ベジェ曲線は、
\begin{align}
P(t) &= B_0
\left(\begin{matrix}
2 \\
0
\end{matrix}\right)
t^0 (1-t)^2 + B_1
\left(\begin{matrix}
2 \\
1
\end{matrix}\right)
t^1 (1-t)^1 + B_2
\left(\begin{matrix}
2 \\
2
\end{matrix}\right)
t^2 (1-t)^0\\
&= B_0 \cfrac{2!}{0!\,(2-0)!}\, (1-t)^2 + B_1 \cfrac{2!}{1!\,(2-1)!}\, t\,(1-t) + B_2 \cfrac{2!}{2!\,(2-2)!}\, t^2\\
&= B_0\,(1-t)^2 + B_1 2t\,(1-t) + B_2t^2
\end{align}
ただし、$ 0 \leqq t \leqq 1 $ とします。$ t $ の値は曲線上の点の位置を表しており、始点なら $ t = 0 $ 、終点なら $ t = 1 $ です。2次ベジェ曲線の始点を $P_1(x_1,,y_1) $ 、制御点を $ P_2(x_2,,y_2) $ 、終点を $ P_3(x_3,,y_3) $ とすると、
\begin{cases}
x(t) = (1-t)^2 x_1 + 2t\,(1-t)\,x_2 + t^2x_3 \\
y(t) = (1-t)^2 y_1 + 2t\,(1-t)\,y_2 + t^2y_3 \\
\end{cases}
次に、始点・制御点・終点の座標を代入します。
\begin{cases}
x(t) = (1-t)^2\times320 + 2t\,(1-t)\times660 + t^2\times768 \\
y(t) = (1-t)^2\times20 + 2t\,(1-t)\times22 + t^2\times40 \\
\end{cases}\\
\begin{cases}
x(t) = -232t^2 + 680t + 320 \\
y(t) = 16t^2 + 4t + 20
\end{cases}
これで、媒介変数 $ t $ の値によって $ x,, y $ 座標が求められるようになりました。最後に線形補間で近似します。ここでは、2次関数の区間を3分割します。分割数を増やせば近似の精度が上がりますが、その分メディアクエリも増えるので多くても10分割までにした方が良いです。3分割する場合、$ 0 \leqq t \leqq 1 $ なので、$ t = \frac{1}{3} $ と $ t = \frac{2}{3} $ のときの座標を求めます。
\begin{cases}
x\left(\cfrac{1}{3}\right) = -232\left(\cfrac{1}{3}\right)^2 + 680\left(\cfrac{1}{3}\right) + 320 = 520.88888... \fallingdotseq 521 \\
y\left(\cfrac{1}{3}\right) = 16\left(\cfrac{1}{3}\right)^2 + 4\left(\cfrac{1}{3}\right) + 20 = 23.11111... \fallingdotseq 23
\end{cases}\\
\begin{cases}
x\left(\cfrac{2}{3}\right) = -232\left(\cfrac{2}{3}\right)^2 + 680\left(\cfrac{2}{3}\right) + 320 = 670.22222... \fallingdotseq 670 \\
y\left(\cfrac{2}{3}\right) = 16\left(\cfrac{2}{3}\right)^2 + 4\left(\cfrac{2}{3}\right) + 20 = 29.77777... \fallingdotseq 30
\end{cases}
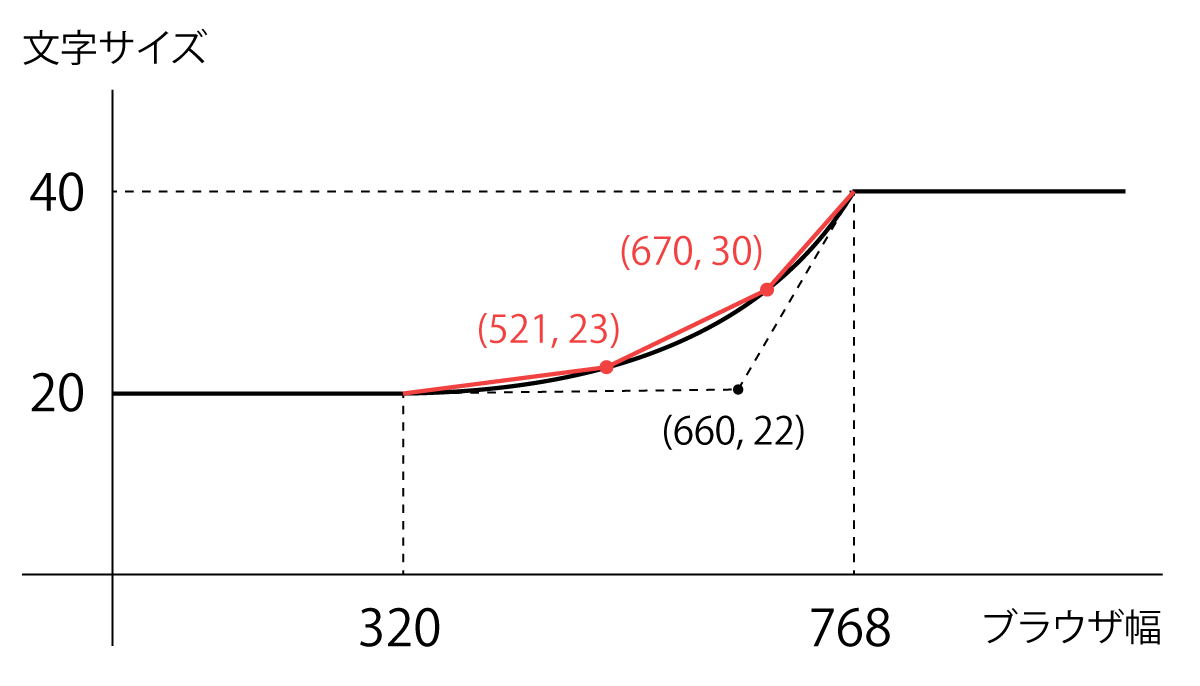
これで座標が求められたので、あとは1次関数のときと同様にして各区間の式を求めます。
// ブラウザ幅 < 320px
body {
font-size: 20px;
}
// 320px ≦ ブラウザ幅 < 521px
@media (min-width: 320px) {
body {
font-size: calc((1 / 67) * 100vw + (1020 / 67) * 1px);
}
}
// 521px ≦ ブラウザ幅 < 670px
@media (min-width: 521px) {
body {
font-size: calc((7 / 149) * 100vw - (220 / 149) * 1px);
}
}
// 670px ≦ ブラウザ幅 < 768px
@media (min-width: 670px) {
body {
font-size: calc((5 / 49) * 100vw - (1880 / 49) * 1px);
}
}
// 768px ≦ ブラウザ幅
@media (min-width: 768px) {
body {
font-size: 40px;
}
}
おわりに
このテクニックを使えば、ブラウザ幅をあまり気にする必要がなくなります。また、今回は font-size プロパティを例にしましたが、数値が使えるプロパティなら line-height margin padding など何でも使えます。
ちなみに1次関数は、最新のCSSである min() max() 関数を使えばより簡略化できます。対応ブラウザはまだ少ないですが...
body {
// min([最大値], max([最小値], [aの値]))
font-size: min(40px, max(20px, calc((5 / 112) * 100vw)));
}
なんとメディアクエリが必要ないのです。さらに最新の clamp() 関数を使えばもっと簡略化できます。
body{
// clamp([最小値], [aの値], [最大値])
font-size: clamp(20px, calc((5 / 112) * 100vw), 40px);
}
CSSでMath系の関数が使えるようになると表現の幅が広がります。CSS Working Groupによると、sin() や cos()、sqrt() 関数なども使えるようになるとのことでとても楽しみです。
僕は現在、tatamiというSassライブラリを制作中です。フロントエンドエンジニアの方達の労力を少しでも軽減させることと、複雑な処理を @include するだけで使えるようにすることが目的です。今回紹介した1次関数も_fluid()関数を使えば簡単に実装できます。今後も様々な機能を追加していく予定です。Issueで機能提案してもらえれば、可能な範囲で実装します。
最後に便利な機能を少しだけ紹介して終わります。
| 機能 | 説明 |
|---|---|---|
| _data-url() | SVGやファイルをBase64エンコード |
| _aspect-ratio() | アスペクト比の固定 |
| _fluid() | 1次関数を利用したレスポンシブな値 |
| _sticky-footer() | スティッキーフッター |
| _font-face() | @font-faceを楽に指定 |
| _readable-color() | 背景色によって見やすい方の文字色を指定 |
| _media() | メディアクエリを楽に指定 |
| _triangle() | 三角形を描画 |
- tatami - A powerful Sass library https://github.com/takamoso/tatami
- Twitter https://twitter.com/takamosoo