はじめに
今年大活躍したWBCや直近のMLBでの大谷翔平選手の投球を見ていて気になったことがありました。
それは、「最近、スイーパーの横の曲がりがさらに大きくなったのではないか?」ということです。
WBC決勝でも、大谷翔平投手のスイーパーは約43cmも曲がっていたとされていましたね。
https://hochi.news/articles/20230323-OHT1T51024.html
元々、大谷翔平投手のスイーパーの横の曲がりは大きいと評されていましたが、最近の2023年ではさらに横の曲がりが大きくなったのでは?とふと思い、それを統計的に検証してみたいと思いました。
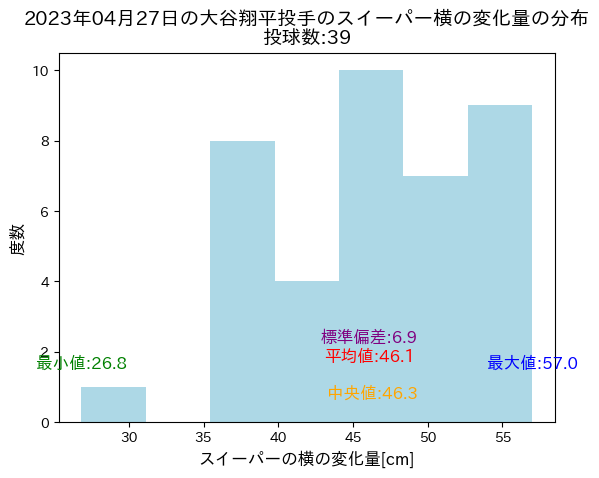
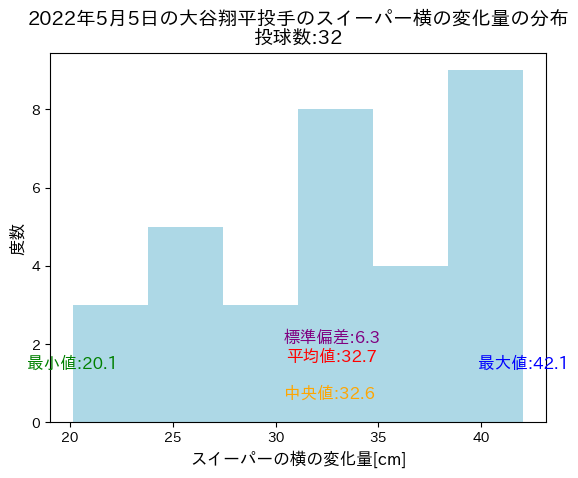
ただ、検証の前に実際にデータにて、2023年04月27日と2022年5月5日において、大谷翔平投手が投げたスイーパーの横の変化量の分布を比較してみました。
ヒストグラムと統計量を見る限り、大谷翔平投手のスイーパーは、2023年の方が2022年よりもスイーパー横の変化量が大きくなっていると考えられそうです。
今回は、上記のヒストグラム導出までの、データ加工を行います。
データ準備
はじめに、2022年と2023年のMLBの大谷翔平投手の投球データを取得します。
データを取得するサイトは以下です。
https://baseballsavant.mlb.com/statcast_search
選手の検索画面で、以下の写真のようにSeasonを2023に指定し、検索を行います。

そうすると、Seasonが2023年におけるMLB各投手が表示されるので、大谷翔平選手を探し(検索で「ohtani」と探すと見つかります)、「Download as CSV」で2023年の大谷翔平選手の投球データをCSVファイルにてダウンロードします。

以上の作業を、2022年の場合でも実施し、2022年と2023年のMLB大谷翔平選手の投球データがCSVファイルにて保存されていることを前提にこれ以降、データ加工を行います。
データ加工
はじめに、今回はPandasを使用して、2つのCSVファイル(2022年と2023年の大谷翔平選手の投球データ)を読み込み、それぞれ"df_2022_ohtani_pitch"と"df_2023_ohtani_pitch"という名前のデータフレームに格納します。
import pandas as pd
df_2022_ohtani_pitch = pd.read_csv('data/2022_MLB_大谷翔平投手の投球データ.csv')
df_2023_ohtani_pitch = pd.read_csv('data/2023_MLB_大谷翔平投手の投球データ.csv')
取得した2022年と2023年のMLB大谷翔平投手の投球データの形状を見てみると、
print("df_2022_ohtani_pitch.shape",df_2022_ohtani_pitch.shape)
print("df_2023_ohtani_pitch.shape",df_2023_ohtani_pitch.shape)
カラムは共に92列あり、2022年は2629行、2023年は522行あることがわかりました。
※ 2023年の投球データが少ないのは、データ取得を行ったのが2023年4月末時点であるためです。
df_2022_ohtani_pitch.shape (2629, 92)
df_2023_ohtani_pitch.shape (522, 92)
ただ、この状態だとカラム数が92個もあって、非常にデータとして扱いにくいです。
試しに、2022年の投球データを読み込んで表示させてみます。
df_2022_ohtani_pitch.head()
| pitch_type | game_date | release_speed | release_pos_x | release_pos_z | player_name | batter | pitcher | events | description | ... | if_fielding_alignment | of_fielding_alignment | spin_axis | delta_home_win_exp | delta_run_exp |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ST | 2022-10-05 | 84.7 | -2.67 | 5.61 | Ohtani, Shohei | 660650 | 660271 | strikeout | swinging_strike | ... | 0 | Standard | 58.0 | -0.033 | -0.204 |
| ST | 2022-10-05 | 83.9 | -2.53 | 5.58 | Ohtani, Shohei | 660650 | 660271 | NaN | swinging_strike | ... | 0 | Standard | 64.0 | 0.000 | -0.062 |
| ST | 2022-10-05 | 84.4 | -2.55 | 5.65 | Ohtani, Shohei | 660650 | 660271 | NaN | swinging_strike | ... | 0 | Standard | 63.0 | 0.000 | -0.046 |
| CU | 2022-10-05 | 74.3 | -1.84 | 6.20 | Ohtani, Shohei | 668843 | 660271 | sac_fly | hit_into_play | ... | 0 | Infield shift | 38.0 | 0.019 | -0.399 |
| ST | 2022-10-05 | 85.6 | -2.49 | 5.58 | Ohtani, Shohei | 640461 | 660271 | double | hit_into_play | ... | 0 | Standard | 65.0 | 0.112 | 0.935 |
上記のように、不要なカラムを読み込んでいることがわかるので、今回は、必要そうな5つのカラム「player_name": "投手名", "game_date": "試合日時", "pfx_x": "横の変化量", "release_speed": "球速", "pitch_name": "変化球名"」のみに絞りました。
# 必要なカラムを選定
df_2022_ohtani_selected_pitch = df_2022_ohtani_pitch[["player_name","game_date","pfx_x","release_speed","pitch_name"]]
df_2022_ohtani_selected_pitch = df_2022_ohtani_selected_pitch.rename(columns={"player_name": "投手名", "game_date": "試合日時", "pfx_x": "横の変化量", "release_speed": "球速", "pitch_name": "変化球名"})
df_2023_ohtani_selected_pitch = df_2023_ohtani_pitch[["player_name","game_date","pfx_x","release_speed","pitch_name"]]
df_2023_ohtani_selected_pitch = df_2023_ohtani_selected_pitch.rename(columns={"player_name": "投手名", "game_date": "試合日時", "pfx_x": "横の変化量", "release_speed": "球速", "pitch_name": "変化球名"})
先頭行を確認します。
df_2022_ohtani_selected_pitch.head()
必要カラム名だけに絞り、またカラム名を日本語で見やすくしました。
| 投手名 | 試合日時 | 横の変化量 | 球速 | 変化球名 |
|---|---|---|---|---|
| Ohtani, Shohei | 2022-10-05 | 1.25 | 84.7 | Sweeper |
| Ohtani, Shohei | 2022-10-05 | 1.41 | 83.9 | Sweeper |
| Ohtani, Shohei | 2022-10-05 | 1.26 | 84.4 | Sweeper |
| Ohtani, Shohei | 2022-10-05 | 0.93 | 74.3 | Curveball |
| Ohtani, Shohei | 2022-10-05 | 1.08 | 85.6 | Sweeper |
さらに、元データでは、横の変化量と球速はアメリカ仕様で、それぞれインチとマイルという単位になっています。
このインチとマイルの単位は、我々日本人としては、なじみが薄いので、それぞれ日本でなじみのあるセンチ(cm)とキロ(km)に変換します。
# インチをセンチに変換
df_2022_ohtani_selected_pitch["横の変化量[cm]"] = df_2022_ohtani_selected_pitch["横の変化量[cm]"] * 30.48
df_2023_ohtani_selected_pitch["横の変化量[cm]"] = df_2023_ohtani_selected_pitch["横の変化量[cm]"] * 30.48
# マイルをキロに変換
df_2022_ohtani_selected_pitch["球速[km/h]"] = df_2022_ohtani_selected_pitch["球速[km/h]"] * 1.60934
df_2023_ohtani_selected_pitch["球速[km/h]"] = df_2023_ohtani_selected_pitch["球速[km/h]"] * 1.60934
出力を確認すると
df_2023_ohtani_selected_pitch.head()
大変見やすくなりました!
| 投手名 | 試合日時 | 横の変化量[cm] | 球速[km/h] | 変化球名 |
|---|---|---|---|---|
| Ohtani, Shohei | 2023-04-27 | -6.7056 | 154.335706 | 4-Seam Fastball |
| Ohtani, Shohei | 2023-04-27 | 10.3632 | 140.656316 | Cutter |
| Ohtani, Shohei | 2023-04-27 | 33.2232 | 113.458470 | Curveball |
| Ohtani, Shohei | 2023-04-27 | -45.4152 | 150.795158 | Sinker |
| Ohtani, Shohei | 2023-04-27 | 36.5760 | 135.023626 | Sweeper |
次に、ある試合日時における投球データの確認を行いたいと思います。
まずは、以下にて大谷翔平選手の登板試合ごとの投球数を確認してみます。
# 大谷翔平選手の登板試合の投球数を確認
df_2023_ohtani_selected_pitch["試合日時"].value_counts()
| 試合日時 | 投球数 |
|---|---|
| 2023-04-05 | 111 |
| 2023-04-21 | 102 |
| 2023-04-27 | 93 |
| 2023-03-30 | 93 |
| 2023-04-11 | 92 |
| 2023-04-17 | 31 |
直近だと、4月27日(日本時間だと4月28日)のアスレチックス戦に大谷選手は先発していまして、球数が93球であると確認できました。

参考url
この23年4月27日の対アスレチック戦における大谷翔平選手の投球内容をグラフも使い確認していきます。
データ可視化
事前に、日本語でmatplotlibを使用すると、文字化けをすることがわかっているので、以下のようにjapanize_matplotlibをインストールしておきます。
!pip install japanize-matplotlib
上記を行った上で以下のコードを実行すると
import matplotlib.pyplot as plt
import japanize_matplotlib
# カラム"変化球名"の値の出現回数を集計
pitch_counts = ohtani_pitch_game_2023_04_27["変化球名"].value_counts()
# 円グラフを描画
fig = plt.figure(figsize=(7, 7))
plt.pie(pitch_counts, labels=pitch_counts.index, labeldistance=1.0, autopct=lambda p: '{:.0f}\n({:.1f}\%)'.format(p * sum(pitch_counts)/100, p), textprops={'fontsize': 10, 'color': 'black'})
plt.title("23年4月27日_対アスレチック戦_大谷翔平投手_変化球の内訳(全投球数:{})".format(sum(pitch_counts)))
plt.show()
23年4月27日の対アスレチック戦における大谷翔平投手の変化球の内訳が円グラフで確認できます。
スイーパーが約41.9%、4シーム(ストレート)が26.9%。投球全体の割合として、やはりスイーパーが大部分を占めているようです。
さて、ここでやっと冒頭の「はじめに」で示した2023年04月27日の大谷翔平選手が投げたスイーパーの横の変化量の分布を描画します。
コードは以下になります。
import numpy as np
# 横の変化量のヒストグラム
horizontal = ohtani_pitch_sweeper_game_2023_04_27["横の変化量[cm]"]
plt.hist(horizontal, bins='auto', color='lightblue')
plt.xlabel("スイーパーの横の変化量[cm]", fontsize=12)
plt.ylabel("度数", fontsize=12)
plt.title(f"2023年04月27日の大谷翔平投手のスイーパー横の変化量の分布\n投球数:{len(horizontal)}", fontsize=14)
mean = horizontal.mean()
median = horizontal.median()
maximum = horizontal.max()
minimum = horizontal.min()
std = np.std(horizontal) # 標準偏差
plt.text(mean, plt.ylim()[1]*0.2, f"平均値:{mean:.1f}", color='red', fontsize=12, ha='center', va='top')
plt.text(median, plt.ylim()[1]*0.1, f"中央値:{median:.1f}", color='orange', fontsize=12, ha='center', va='top')
plt.text(maximum, plt.ylim()[1]*0.18, f"最大値:{maximum:.1f}", color='blue', fontsize=12, ha='center', va='top')
plt.text(minimum, plt.ylim()[1]*0.18, f"最小値:{minimum:.1f}", color='green', fontsize=12, ha='center', va='top')
plt.text(mean, plt.ylim()[1]*0.25, f"標準偏差:{std:.1f}", color='purple', fontsize=12, ha='center', va='top')
plt.tick_params(axis='both', labelsize=10)
plt.show()
以下が上記の結果です。定量的にわかるように、ヒストグラムだけでなく、統計量も表示しました。

また、同様のことを2022年5月5日の試合でも実施しました。
結果は以下のようになりました。
2023年04月27日のスイーパーの横の曲がりの平均は46.1cm、2022年5月5日の方は32.7cmと確認でき、またヒストグラムからも2023年方が2022年よりスイーパーの横の曲がりが大きい分布となっていることが言えそうです。
(冒頭で述べたことの繰り返しになりますが。。)
まとめ・終わりに
単純に、ヒストグラムと統計量を見た感じでは、2023年のスイーパーの横の曲がりは2022よりも大きくなっていると言えそうです。
これが統計的に正しいのかということを、次回ウェルチのt検定という仮説検定を行い、検証を行っていきます。