AtCoder ABC168
2020-05-17(日)に行われたAtCoderBeginnerContest168の問題をA問題から順に考察も踏まえてまとめたものとなります.
後半ではDEFの問題を扱います.前半はこちら.
問題は引用して記載していますが,詳しくはコンテストページの方で確認してください.
コンテストページはこちら
公式解説PDF
D問題 .. (Double Dots)
問題文
あるところに、洞窟があります。
洞窟には$N$個の部屋と$M$本の通路があり、部屋には$1$から$N$の、通路には$1$から$M$の番号がついています。通路$i$は部屋$A_i$と部屋$B_i$を双方向につないでいます。どの$2$部屋間も、通路をいくつか通って行き来できます。部屋$1$は洞窟の入り口がある特別な部屋です。
洞窟の中は薄暗いので、部屋$1$以外の各部屋に$1$つずつ道しるべを設けることにしました。各部屋の道しるべは、その部屋と通路で直接つながっている部屋の$1$つを指すように置きます。
洞窟の中は危険なので、部屋$1$以外のどの部屋についても以下の条件を満たすことが目標です。
その部屋から出発し、「いまいる部屋にある道しるべを見て、それが指す部屋に移動する」ことを繰り返すと、部屋$1$に最小の移動回数でたどり着く。
目標を達成できる道しるべの配置が存在するか判定し、存在するならばそのような配置を$1$つ出力してください。
出力
目標を達成できる道しるべの配置が存在しなければ"No"を出力せよ。
存在する場合、$N$行出力せよ。$1$行目には"Yes"を、$i(2 \leq i \leq N)$行目には部屋$i$の道しるべが指す部屋の番号を出力せよ。
とりあえず,問題が理解しやすかったので,実装したら解けました.
これ,目標を達成できる道しるべの配置は絶対あると思ったので,"No"を出力する記述は書きませんでした(そもそも,"No"になる例が思いつかなかったから,書きようがなかった).
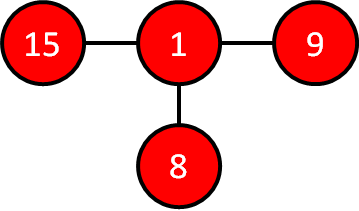
シンプルに適当な入力例を考えます.
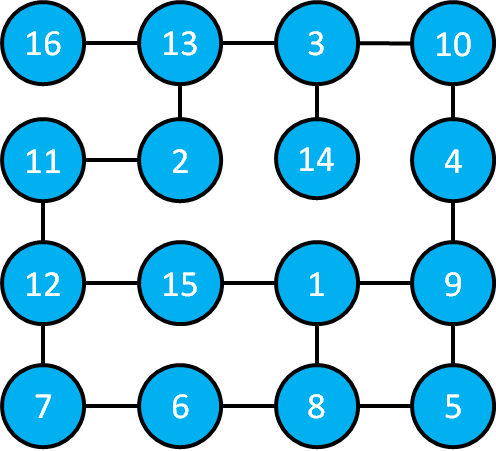
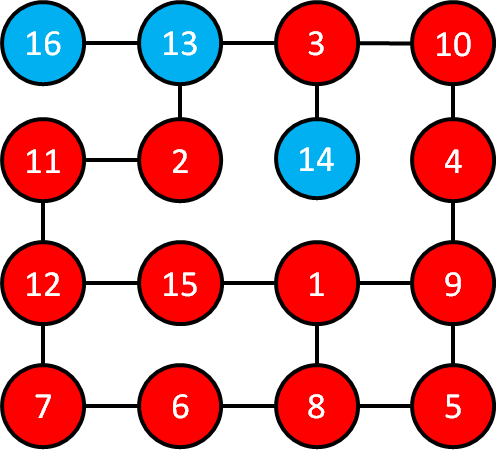
まず,部屋1とつながっている部屋を確認していきます.
これらの部屋1とつながっている部屋8,9,15を深さ1の部屋と考えます.
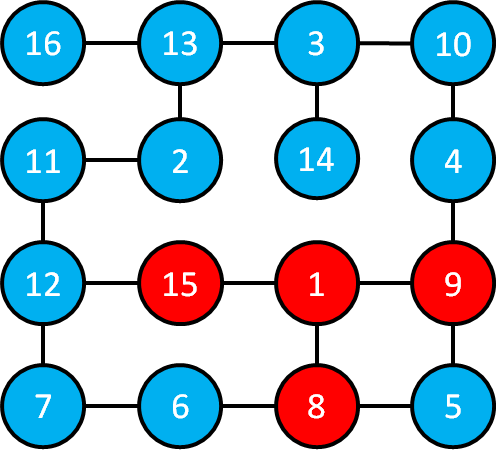
次に,先ほど色を赤く色を塗った部屋を確認していきます.
これらの部屋とつながっている部屋4,5,6,12を深さ2の部屋と考えます.
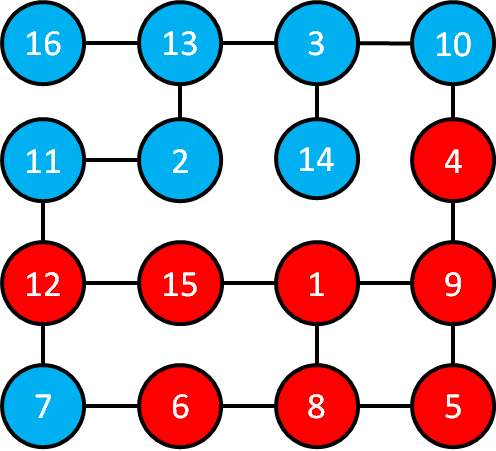
同様に,先ほど色を赤く色を塗った部屋を確認していきます.
これらの部屋とつながっている部屋7,10,11を深さ3の部屋と考えます.
ひたすら繰り返しです.
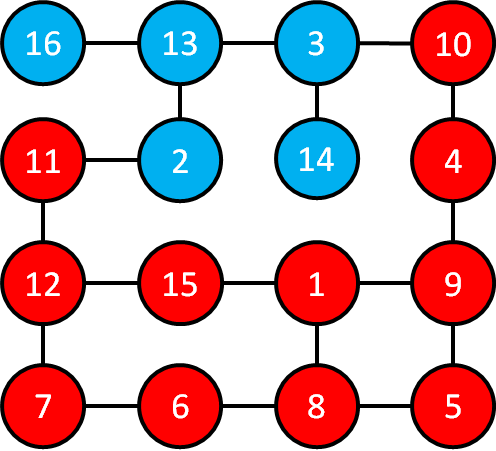
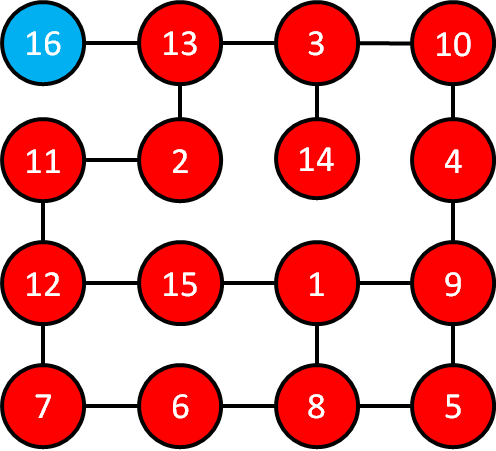
先ほど色を赤く色を塗った部屋を確認していき,これらの部屋とつながっている部屋2,3を深さ4の部屋と考えます.
部屋13,14を深さ5の部屋と考えます.
部屋16を深さ6の部屋と考えます.
これで探索は終わりました.
あとは,一番深い部屋から,一つずつ浅い部屋を選べば,その部屋から部屋1までの最短のルートになります.
実際の実装は,色を塗る段階で答えを部屋ごとに記録していきます.
この解き方をするために,各部屋ごとに,どの部屋とつながっているかの情報をデータ構造として保持しておきます.
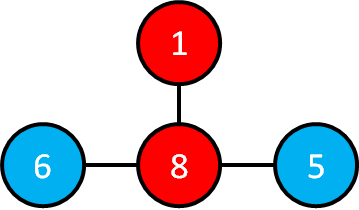
まず,部屋1とつながっている部屋を確認していきます.
これらの部屋1とつながっている部屋8,9,15に道しるべとして,"1"を書き入れておきます.
次に,先ほど道しるべをつけた部屋8,9,15を順にみていきます.
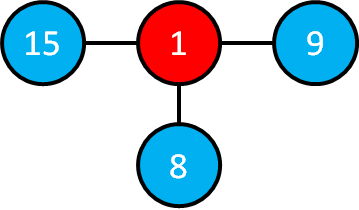
まず,部屋8とつながっている部屋を確認していきます.
ここですでに色が赤になっている部屋は無視して,まだ色が水色の部屋5,6に道しるべとして,"8"を書き入れておきます.
これは,部屋6→部屋8→部屋1でたどれば最短距離で部屋1に戻れます(部屋5も同様).
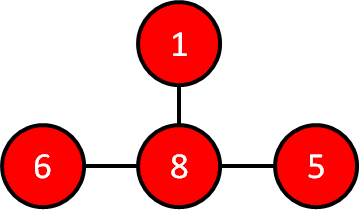
次に,部屋9とつながっている部屋を確認していきます.
ここで先ほどと同様にすでに色が赤になっている部屋は無視して,まだ色が水色の部屋4に道しるべとして,"9"を書き入れておきます.
これは,部屋4→部屋9→部屋1でたどれば最短距離で部屋1に戻れます.
部屋5はすでに赤色で,他のルートで部屋1に戻る最短ルートがあるので無視できます.
このような確認と道しるべの書き入れを行うことで,答えを作ることが可能となります.
n, m = map(int, input().split())
dict_road = {}
dict_room = {}
for i in range(0, m):
a, b = map(int, input().split())
if a in dict_road:
dict_road[a].append(b)
else:
dict_road[a] = [b]
if b in dict_road:
dict_road[b].append(a)
else:
dict_road[b] = [a]
start_list = dict_road[1]
temp_list = []
for no in start_list:
dict_room[no] = 1
temp_list.append(no)
while True:
next_temp_list = []
for no in temp_list:
for next_no in dict_road[no]:
if next_no not in dict_room:
dict_room[next_no] = no
next_temp_list.append(next_no)
if len(next_temp_list) == 0:
break
temp_list = next_temp_list
print("Yes")
for i in range(2, n + 1):
print(dict_room[i])
E問題 ∙ (Bullet)
問題文
$N$匹のイワシが釣れました。$i$匹目のイワシの美味しさは$A_i$、香り高さは$B_i$です。
この中から$1$匹以上のイワシを選んで同じクーラーボックスに入れますが、互いに仲が悪い$2$匹を同時に選ぶことはできません。
$i$匹目と$j(\neq i)$匹目のイワシは、$A_i⋅A_j+B_i⋅B_j=0$を満たすとき(また、その時に限り)仲が悪いです。
イワシの選び方は何通りあるでしょう?答えは非常に大きくなる可能性があるので、$1000000007$で割ったあまりを出力してください。
珍しくD問題がかなり早い段階で通せたので,E問題も解きたかったですが,結局解けませんでした.
仲が悪い2匹のイワシの組み合わせを求めることまでやってタイムオーバーでした.
F問題 Three Variables Game
問題文
無限に広がる草原があります。
この草原上に、大きさが無視できるほど小さい$1$頭の牛がいます。牛の今いる点から南に$x\ \mathrm{cm}$、東に$y\ \mathrm{cm}$移動した点を$(x,y)$と表します。牛自身のいる点は$(0,0)$です。
また、草原には$N$本の縦線と$M$本の横線が引かれています。
$i$本目の縦線は点$(A_i,C_i)$と点$(B_i,C_i)$とを結ぶ線分、$j$本目の横線は点$(D_j,E_j)$と点$(D_j,F_j)$とを結ぶ線分です。
牛が線分を(端点を含め)通らない限り自由に動き回れるとき、牛が動き回れる範囲の面積は何$\mathrm{cm^2}$でしょうか。この範囲の面積が無限大である場合は代わりに"INF"と出力してください。
このあたりが解ける日がはたして来るのだろうか…
後半も最後まで読んでいただきありがとうございました.