AtCoder ABC161
2020-04-04(土)に行われたAtCoderBeginnerContest161の問題をA問題から順に考察も踏まえてまとめたものとなります.
後半ではDEFの問題を扱います.前半はこちら.
問題は引用して記載していますが,詳しくはコンテストページの方で確認してください.
コンテストページはこちら
公式解説PDF
D問題 Lunlun Number
問題文
正の整数$X$が以下の条件を満たすとき、$X$はルンルン数であると言います。
・$X$を(leading zeroなしで)十進数表記した際に、隣り合うどの2つの桁の値についても、差の絶対値が1以下
例えば、1234, 1, 334などはルンルン数ですが、31415, 119, 13579などはルンルン数ではありません。
正の整数$K$が与えられます。小さい方から K 番目のルンルン数を求めてください。
$1 \leq K \leq 10^5$だったので,小さいものからルンルン数を再帰関数で数えていけば間に合うと思って,プログラム書いたら解けてすごく嬉しかった.
解けたときはルンルンだったが,問題見たときはまったくルンルンしなかった.
提出したコードをそのまま載せます.
def check(mae, keta, count, k):
if keta == 0:
count += 1
if count == k:
ans = mae
else:
ans = -1
return count, ans
if mae == 0:
count, ans = check(0, keta - 1, count, k)
if ans >= 0:
ans += mae * 10 ** keta
return count, ans
count, ans = check(1, keta - 1, count, k)
if ans >= 0:
ans += mae * 10 ** keta
return count, ans
elif mae == 9:
count, ans = check(8, keta - 1, count, k)
if ans >= 0:
ans += mae * 10 ** keta
return count, ans
count, ans = check(9, keta - 1, count, k)
if ans >= 0:
ans += mae * 10 ** keta
return count, ans
else:
for i in [-1, 0, 1]:
count, ans = check(mae + i, keta - 1, count, k)
if ans >= 0:
ans += mae * 10 ** keta
return count, ans
return count, ans
k = int(input())
if k < 10:
print(k)
else:
count = 9
flag = 0
for keta in range(2, 1000):
for sento in range(1, 10):
count, ans = check(sento, keta - 1, count, k)
if ans >= 0:
print(ans)
flag = 1
break
if flag == 1:
break
プログラムを書いたときの考えとしては,$m$桁のルンルン数を作る場合,樹形図で最高位から数字決めてけば作れるじゃんと思って,再帰関数を思いついた.
例えば1から始まる3ケタのルンルン数1**は以下の図のように求めることができる.
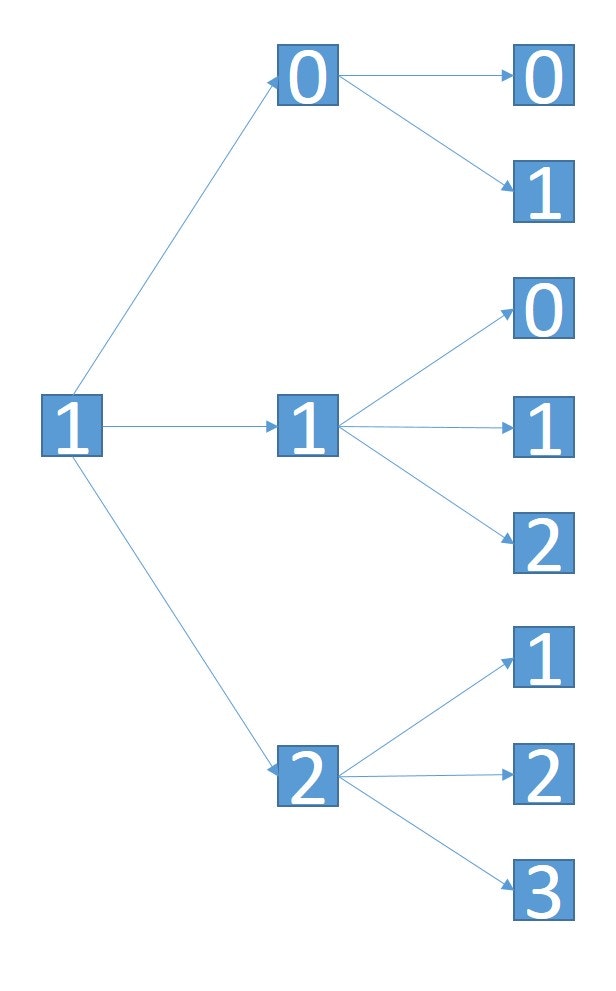
注意すべきは,0のときと9のときの分岐が2種類であることで,それにさえ注意できればあとは,数えるための変数と現在何桁目を考えているかの情報を関数に入力し,貪欲に探していけば答えを時間内に求めることが可能である.
E問題 Yutori
問題文
高橋君は明日からの$N$日間のうち$K$日を選んで働くことにしました。
整数$C$と文字列$S$が与えられるので、次の2つの条件を満たすようにして働く日を選びます。
・ある日働いたら、その直後の$C$日間は働かない
・$S$の$i$文字目が$x$のとき、今日から$i$日後には働かない
高橋君が必ず働く日をすべて求めてください。
コンテスト時は慌ててたので,「・$S$の$i$文字目が$x$のとき、今日から$i$日後には働かない」の意味を正しく読み取れずすぐに次の問題いきました.
終わった後に解説読んで,読み間違いに気づきましたが,読み間違えていなくても,今の自分には解けなかったと思うので,また一つ学びを得ることができました.
このあたりはもう解説に書いてあることに気がつけるような経験を積んでるかどうかな気がしました.提出されたコードの中で早い段階でAC通していたKiri8128さんのコードを参考にさせてもらいました.@kiri8128
n, k, c = map(int, input().split())
S = [1 if a == "o" else 0 for a in input()]
count = 0
X = [0] * n
Y = [0] * n
i = 0
while i < n:
if S[i]:
count += 1
X[i] = 1
# print(i+1)
i += c + 1
else:
i += 1
if count > k:
exit()
i = n - 1
while i >= 0:
if S[i]:
Y[i] = 1
# print(i+1)
i -= c + 1
else:
i -= 1
for i in range(0, n):
if X[i] and Y[i]:
print(i + 1)
Sの受け取り方とか参考になりました.
あとは,本番この問題を見たときに解き方を思いつくようになる方法はわからないけど,とにかく多く問題解くことが大事な気がするので精進します.
解説読んでもわからない人のためにprint(i+1)をコメントアウトしていたので,そのコメントアウトを外して,例題を解くといろいろと見えてくるものがあると思います.下記に示す入力例1を例に挙げる.
11 3 2
ooxxxoxxxoo
一つ目のfor文の中のprintによる出力は,1, 6, 10となり,二つ目のfor文の中のprintによる出力は,11, 6, 2となります.
したがって答えは6となります.これらを他の例も同様にやってみると答えが出る理由が理解しやすいと思います.(文章でのいい説明が思いつきませんでした(汗))
F問題 Division or Subtraction
問題文
正整数$N$が与えられます。
2以上$N$以下の整数$K$を決めて、$N$が$K$未満になるまで次の操作を繰り返し行います。
・操作:$N$が$K$で割り切れるとき、$N$を$N/K$に置き換える。そうでないとき、$N$を$N−K$に置き換える。
最終的に$N$が1になるような$K$の決め方は何通りありますか?
コンテスト時はE問題を早々に切り上げF問題に挑みました.理由は入力例2が3141であり,$K$は3141と3140がまず答えに含まれることに気づき,3140が答えになるってことは,1570, 785...あたりで$N-1$の約数は全て答えに含まれることはわかりました.
「2, 4, 5, 10, 20, 157, 314, 628, 785, 1570」
ここから,入力例1の6に$K=2$が含まれているのをどうやって数えるかわからずタイムオーバー(汗).
少し考えたら,$N$の約数が条件を満たすかどうかを確かめるだけだった.
$K$候補は約数となるので割れるところまで,ガンガン割り算していって割れなくなったら余りを調べて1ならば$K$を何回か引けば1になるので条件に当てはまることがわかる.
def make_divisors(n):
divisors = []
for i in range(2, int(n**0.5)+1):
if n % i == 0:
divisors.append(i)
if i != n // i:
divisors.append(n//i)
return divisors
n = int(input())
if n == 2:
print(1)
elif n == 3:
print(2)
elif n == 4:
print(3)
else:
count = 2
check_list = make_divisors(n-1)
count += len(check_list)
check_list = make_divisors(n)
for k in check_list:
temp_n = n // k
while(True):
if temp_n % k == 0:
temp_n = temp_n // k
elif temp_n % k == 1:
count += 1
break
else:
break
print(count)
チキンなのでnが小さいときは,場合分けしてますが,しなくても解けるはずです.
count = 2の内訳は$N$と$N-1$の二つです.
このF問題が時間内に解けるようにはなりたいので,頑張って続けていこうと思います.
後半も最後まで読んでいただきありがとうございました.