本記事の構成は大きく二つに分かれています。茶番を混ぜて、隠れマルコフモデルってどんなものなのかを説明する前半部分と、PRMLを参考にJuliaでモデルの実装を行う後半部分です。
なので、茶番はどうでもいいよ、実装だけ見たいという方はこちらへどうぞ。
注意点として、モデルの実装を行いますが、詳しい式変形を追うことはしません。式変形を知りたい方は、ほかの記事を見ることをお勧めします。
では前半スタートです。
いかさまカジノ
給料日。世のサラリーマンが今日くらいはと羽目を外す日でもある。IT企業に働いている彼もその例にもれない。
岩小田「今月もようやく給料日だよ、、、。先月はアプリのリリースがあってかなり忙しかったから、今月の給料は期待できるぞ」
予想通り、口座にはいつもよりもたくさんの諭吉さんがいらっしゃっていた。
普段なら、給料日だろうがさっさと家に帰って任〇堂のスローライフゲームを嗜む岩小田だが、今日ばかりは様子が違った。
帰路にはつかず、最近できたカジノにやってきたのだ。
岩小田「ここが遼薫さんが言っていたカジノか。島クリの参考にしようと思ってきたけど意外と面白そうだな。給料も入ったし少し遊んでいくか」
会社の同僚である遼薫は、よく業務中に5ちゃんねるを徘徊している。仕事中にいかがなものかと思うが、彼女はゲームの最新情報をいち早く見つけてきてくれるので、岩小田としてはもっとやれといったところ。
岩小田はゲームのアップデートに間に合わせるためなら有休の取得も厭わないほどのゲーマーなのだ。
少々気合の入った角刈り頭をひっさげて、煌びやかなネオンの中へ消えていった。
パチンコ店くらいのノリで足を踏み入れたのだが、すぐに店内の雰囲気に飲まれて岩小田が入口付近できょろきょろとしていると、見かねたディーラーの一人が岩小田に話しかけてきた。
ディーラー「何かお困りですか?」
岩小田「カジノは初めてでこういったゲームはほとんどやらないんだが、なにかおすすめはあるだろうか?」
ディーラー「はい!初めての方でも簡単にできる当店オリジナルのゲームがあります」
岩小田「じゃあ、それでお願いしようかな」
ディーラー「畏まりました。それではあちらにあるテーブルに座って少々お待ちください」
ディーラーにそう促され、岩小田はフロアの端に追いやられたように鎮座しているテーブルに向った。テーブルについて、幾ばくも無くお待たせしましたと、先ほどのディーラーが現れた。
ディーラー「それでは早速ですがルール説明に移りたいと思います。そのあとに簡単なデモンストレーションを行いましょう」
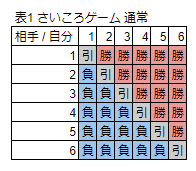
ルールは全く難しくない。デモンストレーションを行うまでもないような内容だった。改めてルールを整理するとこんな感じだろうか。
ルール説明
- プレイヤーは2人
- さいころをお互いに振り数字の大きいほうが勝ち
- 同点の場合、プレイヤーの勝ち
- 規定ゲーム数を行い勝ち点の多いほうの勝利となる
- 勝ち点に応じて支払いが行われる
注目したいとこはこの一文だろう。同点の場合、プレイヤーの勝ち これは相当こちら側が有利である。初心者向けと言っていただけあって勝たせてくれるのだろうか?
伺うような視線をディーラーにやると、その通りですと言いたげな顔をしてこう言った。
ディーラー「もうお気づきかと思いますが一応このゲームはお客様が有利になるように設計されています。さいころの出目の組み合わせは全部で36通りです。勝負に勝つパターンは相手よりも出目が大きい場合の15通りです。これはお互いにとって全く同じ条件でとてもフェアな状態といえます」
ディーラー「しかし今回のゲームは引き分け部分の6パターンもお客様の勝ちパターンになります!つまり、お客様の勝ちパターンは通常の勝ちパターンの15通り+引き分けのパターン、6パターンの合計21パターンになります。単純に考えると21/36の確率でお客様の勝ちです!これはとてもお客様に有利なゲームではないでしょうか?」
岩小田「確かにそうですね。でもどうしてこんなに有利にしてくれるんでしょうか。これだとお店は儲からないのでは?」
当然の疑問をディーラーに投げかけると柔和な笑顔でこう返す。
ディーラー「確かにこれではお店は儲からないでしょう。しかし、これを機にお客様が当店を御贔屓にしていただければ、我々も嬉しい限りです」
一瞬騙されているんじゃないかと思った岩小田であったが、そういうものかと思いなおし、今はゲームを楽しむことにした。
岩小田「それなら遠慮なく。今回は稼がせてもらおうかな」
ディーラー「それではゲームを始めたいと思います」
ディーラーがゲームの開始を告げ、岩小田はさいころを振り始めるのであった。
==================== 翌日 ====================
重い瞼を擦りながら岩小田が自席につくと、すでに出社していた遼薫が隣から声をかけてきた。
遼薫「そういえば、以前君にカジノの話をしたじゃないか。興味ありげな雰囲気を醸していたから一言忠告しておこうと思って」
岩小田「それはいったいどんなアドバイスなんだい?もっとカジノには昨日すでに行ってしまったから手遅れかもしれないけど」
遼薫「それは一足遅かったみたいだね。変なさいころゲーム吹っ掛けられたら気をつけろよって言おうと思って。いや何、所詮ネットのうわさ程度の話さ気にしないでくれ。」
寝ぼけていた頭が急に冷えていく。先ほどまで今日は何時間さぼれるか試算していたのだがそんなのはどこかへ消えてしまった。
岩小田「へんなさいころゲーム?さいころのゲームなら昨日やったが、あれは良くなかったのかい?」
遼薫「いや、そういうわけではないんだ。ちなみにそのゲームは勝てたのかい?」
岩小田「いや、負けたよ。でもそんなにひどい負け方はしてないかな」
そうか、と一言いい遼薫はパソコンに体を向き直し何やら調べ物を始めたようだ。それを見ながら岩小田は自己弁護するように昨日の出来事を説明し始めた。一通り話し終えたとこで、遼薫は再びこちらに向き直りこう言った。
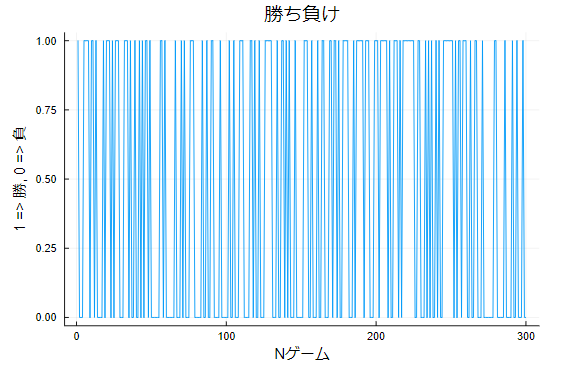
遼薫「まずこれを見てくれ。これは君と同じさいころのゲームをした人が残した記録をプロットしたものだ。ちなみにこの時の成績は、勝:136、負:164」
岩小田「なにも変なとこないんじゃないか?」
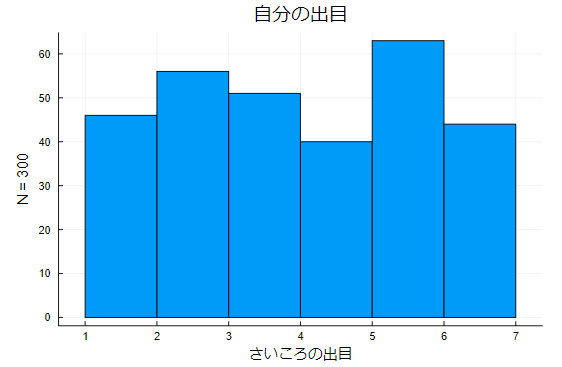
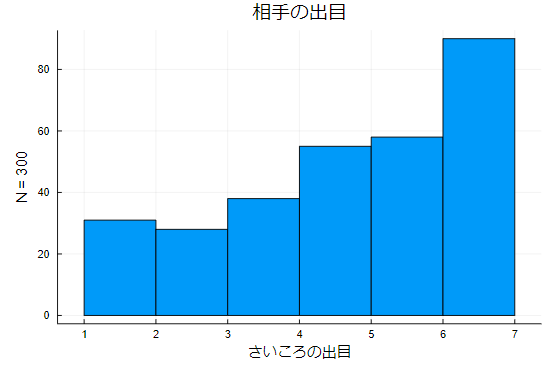
遼薫「では、次にさいころの出目のヒストグラムを見てもらう。まずはプレイヤー側のヒストグラムだ」
遼薫「次にカジノ側」
岩小田「あれ?さすがにこれはおかしくないか?同じさいころ使ってるなら似たようなヒストグラムになるはずだろ?」
遼薫「そうだね。勝ち負けだけ見ると一見普通に見えるんだけど、グラフはそうではないと言っているね。もちろん、偶然さいころの出目が偏ったという可能性も踏まえて適合度の検定も行った。検定の結果は有意であった。つまり、さいころの出目が偏っている可能性があるということだ」
岩小田「け、検定?俺、統計学は苦手なんだよ」
少し大袈裟に頭を抱えてみせるが、遼薫は特に気にした様子もなく続ける。
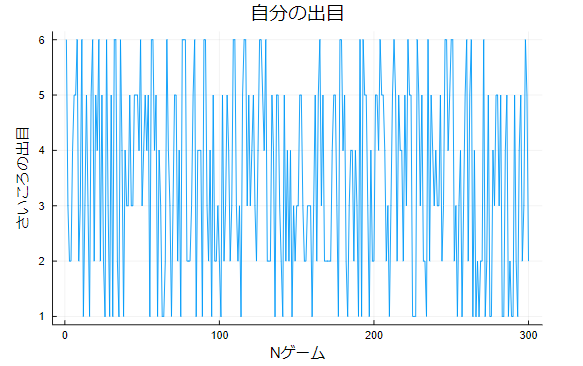
遼薫「検定を使わずとももう少し違う見方をすれだけで、さいころの出目がおかしいことがわかる思う。次は横軸をNゲーム目にして、縦軸をさいころの出目にしてプロットしたものだよ。さっきと同じようにまずはプレイヤー側のグラフを見てみよう」
岩小田「穿った見方をすれば、150~170ゲームあたりが怪しい気がするが」
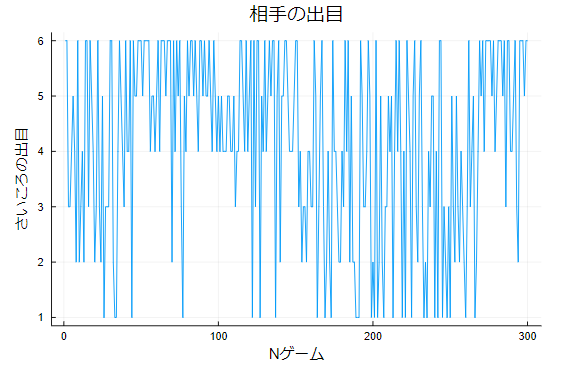
遼薫「ではカジノ側を見てみよう」
岩小田「え!50ゲーム目くらいから120ゲーム目くらいまでの間、明らかに4以上の出目が多く出てる!」
遼薫「これと見比べるとプレイヤー側は通常のさいころが出せそうな出目の範囲だと言えそうだね」
岩小田「たまたま運が悪かったから、負けたのだと思ったけどそうじゃなかったのか」
岩小田は本当の意味で頭を抱えたくなったが、過ぎたことを気にしても仕方ないのだ。
遼薫「少なくとも私はこのゲームのルールでカジノが普通に勝つのは厳しいかなと思っているよ。ヒストグラムとさっきの出目のプロットを考慮すると、おそらく重心の偏ったさいころをカジノ側がゲームの途中ですり替えているんじゃないかな?」
岩小田「全然気づかなかったよ。データを可視化するだけでこんなにもわかることがあるんだね」
遼薫「じゃあ、ついでだからもう少し面白い話をしよう」
といい、机の引き出しから二種類のさいころを取り出した。
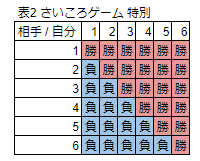
遼薫「ここに白色のさいころと赤色のさいころがある。赤色が重心が偏っている所謂いかさまさいころだと思ってくれ。さっきまでの話で次のような仮定を置くことができる」
- カジノ側は通常さいころと、いかさまさいころを使用している。
- これらのすり替え頻度はそれほど多くない。むしろ一度さいころをチェンジするとそのまましばらく使い続ける傾向がある。
岩小田「いかさまさいころが複数の可能性はないの?」
遼薫「もちろんその可能性もあるが、ここでは一旦いかさまさいころは1個だけであるとしよう。この時私たちは、今のゲームで使用されたさいころが、どちらのさいころなのかということに興味が出てくると思う」
遼薫はそう言いながら後ろ手でさいころを隠し、一個を目の前に放った。さいころは赤かった。
岩小田「赤色ということは、いかさまさいころということだね」
遼薫「その通り。でも実際上は見た目だけで、さいころを区別することは叶わない。私たちが利用できるのは、今振ったときに出た出目と、今までのゲームで出た出目のデータだけ」
岩小田「それだけで、さいころの区別をつけられるというのかい」
半信半疑な顔で遼薫を見ると、ずいっと目の前にパソコンの画面を見せてきた。
遼薫「それを可能にするのが"隠れマルコフモデル"なんだ。音声認識や自然言語処理などでも利用されるね」
岩小田「なんか難しそうな話になってきたな」
頭が痛くなってきたいった岩小田に対して、そこまで難しい話ではないから安心してくれ、と笑いながら遼薫は話す。
遼薫「まずは隠れマルコフモデルでどんな結果を出せるかを見てみようか」
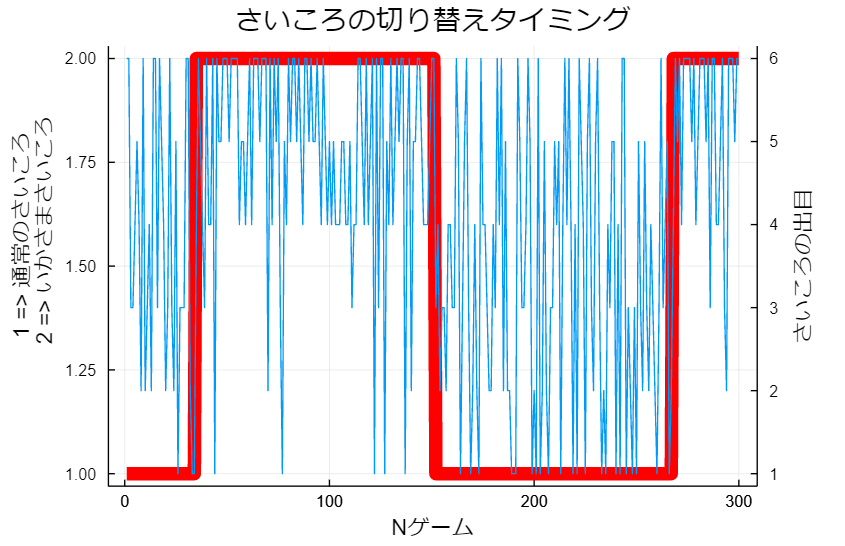
遼薫がパソコンのキーを何回か叩くとグラフが目の前に現れる。
岩小田「どうやって見ればいいんだ?」
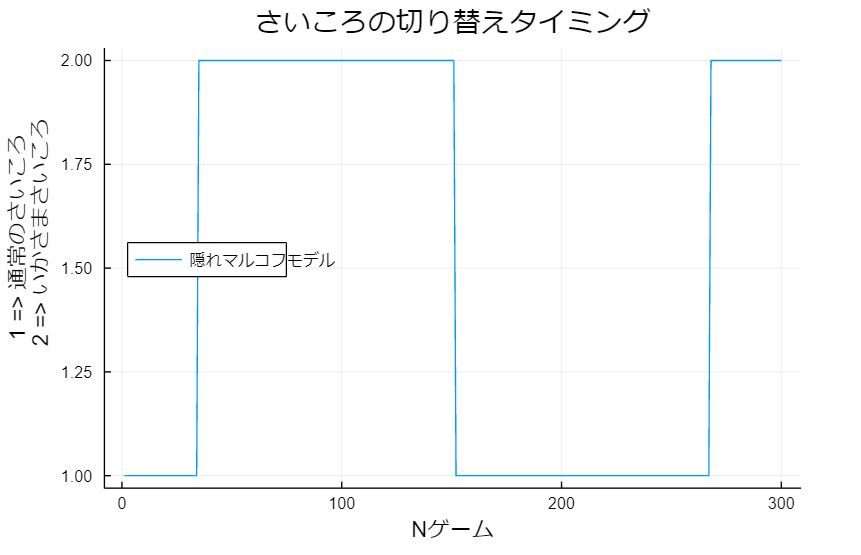
遼薫「グラフが1にあるときは通常のさいころを使っていて、2にあるときはいかさまさいころを使っているという風に見るよ」
岩小田「これ、カジノ側のさいころの出目と重ねて見れたりできないかな?」
それは面白い試みだねと言いながら、カチャカチャとキーを叩く。数秒もしないうちにグラフが出来上がった。
遼薫「さっき君が50~120あたりが怪しいと言っていたが、まさにその通りだったね」
岩小田「統計学ってすごいんだね。何でもわかっちゃうじゃないか」
遼薫「おっと、その思想は危ないな。今回の結果も、"限られたデータ"を使って、さらに"勝手に私たちがいかささいころが一個だと仮定"し、モデルを作成しただけに過ぎないんだ。常に、私たちが仮定した私たちのモデルが出した結果ということを意識しないといけないよ」
岩小田「統計学はお墨付きを得るための道具ではないということだね」
遼薫「その通りだよ。ちなみに、私がこのさいころゲームが何かおかしいと思ったのには理由があってだね。勝率21/36で300回勝負したときの勝利数は二項分布で厳しめに見積もっても、153~197の間に収まるとういう結果が出たんだ。つまり、この条件ならほとんど負けるわけないわけだ」
岩小田「それも検定の一種だよね。俺も苦手意識持たずに勉強しなおそうかな。あ、それじゃあ、この場合は。。。」
業務をほっぽりだして、統計学について話をしていた二人が怒られるのはまた別な話である。
fin
前半終了
上記の物語を書くにあたって試行錯誤したコードのを以下のGistに挙げておきます。隠れマルコフモデルの計算にはHMMBase.jlというJuliaのパッケージを使用しました。
なお、物語の都合上きれいなプロットが出るとこまで乱数を引き直したので、Gistに挙げたコードに再現性はありません。ご了承ください。
隠れマルコフ連鎖とは
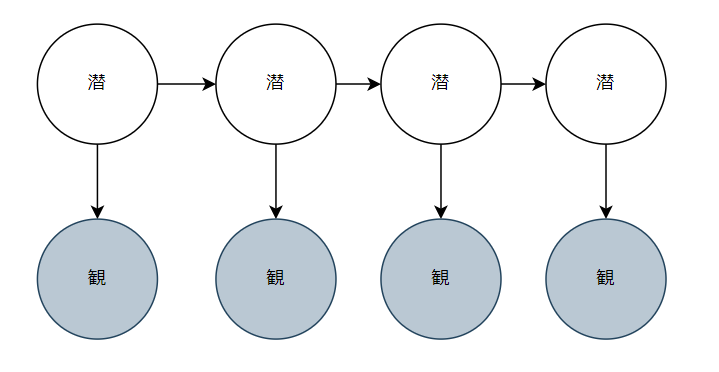
状態空間モデルにおいて潜在変数が離散変数である場合のモデルを、隠れマルコフモデルといいます。グラフィカルモデルで考えると以下のような図になります。
潜在変数と観測値の両方がガウス分布に従う場合のモデルを線形動的モデルといいます。
「潜」は潜在変数を「観」は観測値を表します。なお、潜在変数が離散であることを要求するだけで、観測値は離散であっても連続であっても構いません。
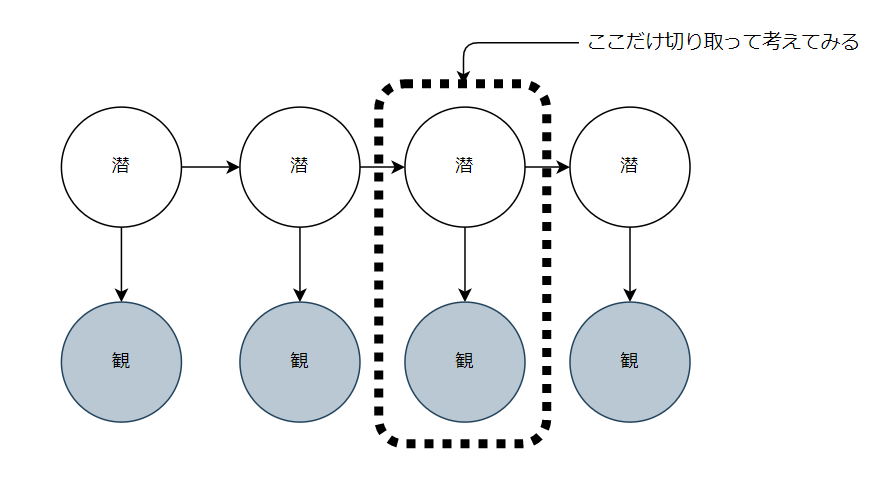
ではここで、上記グラフの、ある時点を切り取って考えてみましょう。
これだけ見ると混合分布になっていることがわかります。つまり隠れマルコフモデルは混合分布の拡張としても見ることができます。
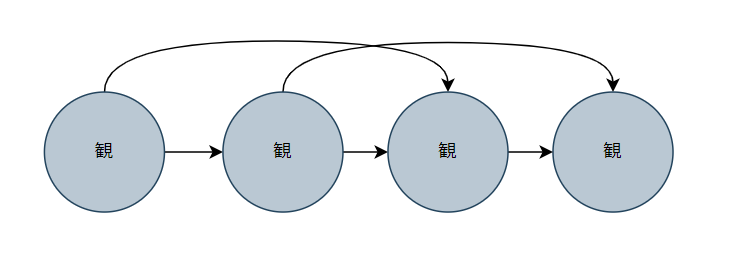
そもそもマルコフモデルってなんなのっていうとグラフィカルモデルで表すとこんな感じです。
これはマルコフモデルの二次マルコフ連鎖です。よくデータは独立同分布に従うとか仮定を置くと思うのですが、系列データは過去のデータの影響を少なからず受けています。それを表すために、過去の観測値から矢印がひっぱられています。
あれれ?これってどこかで見たことありますね。そうです、自己回帰モデル(ARモデル)ですね。ARモデルは時系列分析をすると一番最初に学ぶモデルだと思いますが、マルコフモデルの一種として解釈することもできるんです。
隠れマルコフモデル(Hidden Markov Model, HMM)の実装
さて、隠れマルコフモデルの実装ですが、今回の記事で扱う内容とそうでは内容を先にまとめておこうと思います。
-
扱う内容
- フォワード_バックワードアルゴリズム(Baum-Whelch アルゴリズム)
- 出力分布がガウス分布場合のHMM
-
扱わない内容
- 積和アルゴリズム
- スケーリング係数
- Viterbiアルゴリズム
- ガウス分布以外の出力関数
実装するメソッド
では実装するメソッドを大まかに抽出してみましょう。
- 学習を行うメソッド(fit関数)
- フォワードの計算
- バックワードの計算
- 2つの連続した潜在変数の事後確率分布の計算
- パラメータ更新の計算
fit関数内でEMアルゴリズムの計算を行っていき、詳しい計算はメソッドに分けて計算していく方針で行きたいと思います。
fit関数の実装
fit関数について特筆するところはありません。ただEMアルゴリズムの収束をパラメータの更新幅が閾値以下になると終了するというコードを書いたのですが、いかんせんそれだと収束がうまくいかなかったのでコメントアウトしてあります。
function fit( m::HMM, X; maxiter::Int=100, thres=10^-10 )
省略
# 尤度関数の収束をチェック
likeli_val[n] = sum( α.z[:,end] )
# if abs( sum( α.z[:,end] ) - old ) < thres
# @show "パラメータの変化量が閾値以下になったので学習を終了する. n : $n"
# break
# else
# old = sum( α.z[:,end] )
# end
省略
end
Eステップ
Eステップは事後確率分布を計算します。フォワード_バックワードアルゴリズムの実装をしてしまえば、2つの連続した潜在変数の事後確率分布は簡単に計算できます。
なので、潜在変数の事後確率分布をきちんと整理することを意識して実装しました。
フォワード_バックワードアルゴリズムは再帰構造をもつアルゴリズムです。なので再帰関数を定義していくことになるのですが、最近学んだ Function-like object という書き方で実装しました。Function-like objectについてはJulia公式がわかりやすいと思います。
簡単にですが、例を挙げてFunction-like objectを解説します。
まず、準備するものが2つあります。
- struct
- 1で定義したstructを引数とする関数
# 1.
mutable struct message
msg
end
# 2.
function (str::message)()
str.msg = "messageを書き換えたよ!"
return
end
# ここからFunction-like objectの呼び出し
# まずはstructのインスタンスを作る
obj = message("こんにちは")
obj.msg # こんにちは
# 通常objはメソッドを持たないが、次のようにして先ほど定義した関数を呼び出すことができる
obj()
obj.msg # messageを書き換えたよ!
ちなみに私がFunction-like objectを使用したのはfit関数内にα以外の名前でフォワードを計算させたくなかったからです。αという名前で値を保存して、αという名前でフォワードを計算したかったのでこちらの書き方を採用しました。
以下fit関数の該当箇所の抜粋
function fit( m::HMM, X; maxiter::Int=100, thres=10^-10 )
省略
α = alpha( zeros( K, N ) )
β = beta( zeros( K, N ) )
likeli_val = zeros(maxiter)
for n in 1:maxiter
@show "iter : $n"
#== E step ==#
# αとβの計算
α( N, p, X )
β( 1, p, X )
# PRML(13.33)
γ = α.z .* β.z ./ sum(α.z[:,end])
省略
end
mutable struct alpha{R}
z::Matrix{R}
end
function (forward::alpha)( n, p, X )
# パラメータをアンパック
( ; K, A, π, μ, Σ ) = p
# 潜在変数で条件づけられた出力関数の確率密度を計算
prob = [ pdf( MvNormal( μ[:,k], Σ[:,:,k] ), X[:,n] ) for k in 1:K ]
if n == 1
# PRML(13.37)
α₁ = π .* prob
forward.z[:,n] = α₁
return α₁
else
# PRML(13.36)
αₙ = A' * forward( n - 1, p, X ) .* prob
forward.z[:,n] = αₙ
# HACK: ::VecOrMat{ Float64} となって強調色が出る
# return n == N ? forward.z : αₙ
return αₙ
end
end
Function-like objectのメリットとして、クロージャのように扱えることがあげられます。Juliaのクロージャは型伝播がうまくいかず、パフォーマンスが落ちてしまいます。
クロージャの型伝播について言及されている記事はこちらです。
具体的な例として、フィボナッチ数列を例にFunction-like objectの実装を行った例がこちらです。
Mステップ
Mステップはパラメータの更新です。update_hogehogeと書いてある関数がそれにあたります。
ぱっと見でわかりづらそうな、遷移行列のパラメータ更新だけ取り上げたいと思います。まずはコードがこちら。
update_transition_prob( zₙzₙ₋₁ ) = ( sum( zₙzₙ₋₁, dims=3 ) ./ sum( sum( zₙzₙ₋₁, dims=3 ), dims=2 ) )[:,:]
更新式はこちら。PRML式13.19
A_{jk} = \frac{\Sigma_{n=2}^N \zeta(z_{n-1,j}z_{n,k})}{\Sigma_{l=1}^K \Sigma_{n=2}^N \zeta(z_{n-1,j}z_{n,l})}
zₙzₙ₋₁のサイズは状態数をK、サンプル数をNとすると、K*K*(N-1)の行列です。
ここでK=2を考えてみましょう。この時に具体的に和の記号を解くと、Aj1とAj2は分母が等しいことがわかります。つまり分母は、A11+A12とA21+A22を成分に持つ縦ベクトルを横に並べたK*Kの行列です。
全体のコード
module Q
using Distributions
using LinearAlgebra
using Clustering
struct HMM
n_state
end
"""
n_state : K
A : K * K
π : K
μ : D * K
Σ : D * D * K
γ : K * N
likeli_val : N
"""
struct ResultsHMM
n_state
A
π
μ
Σ
γ
likeli_val
end
function fit( m::HMM, X; maxiter::Int=100, thres=10^-10 )
D, N = size(X)
old = Inf
# 変数初期化
p = init_params( m, X )
( ; K, A, π, μ, Σ ) = p
γ = zeros( K, N )
α = alpha( zeros( K, N ) )
β = beta( zeros( K, N ) )
likeli_val = zeros(maxiter)
for n in 1:maxiter
@show "iter : $n"
#== E step ==#
# αとβの計算
α( N, p, X )
β( 1, p, X )
# PRML(13.33)
γ = α.z .* β.z ./ sum(α.z[:,end])
# PRML (13.43)
zₙzₙ₋₁ = poster_zₙzₙ₋₁(α.z, β.z, p, X)
#== M step ==#
π = update_π(γ)
A = update_transition_prob( zₙzₙ₋₁ )
μ, Σ = update_emission_prob( γ, X, K )
# 尤度関数の収束をチェック
likeli_val[n] = sum( α.z[:,end] )
# if abs( sum( α.z[:,end] ) - old ) < thres
# @show "パラメータの変化量が閾値以下になったので学習を終了する. n : $n"
# break
# else
# old = sum( α.z[:,end] )
# end
# パラメータを格納している名前付きタプルを更新
p = ( K=K, A=A, π=π, μ=μ, Σ=Σ )
end
ResultsHMM( K, A, π, μ, Σ, γ, likeli_val)
end
mutable struct alpha{R}
z::Matrix{R}
end
function (forward::alpha)( n, p, X )
# パラメータをアンパック
( ; K, A, π, μ, Σ ) = p
# 潜在変数で条件づけられた出力関数の確率密度を計算
prob = [ pdf( MvNormal( μ[:,k], Σ[:,:,k] ), X[:,n] ) for k in 1:K ]
if n == 1
# PRML(13.37)
α₁ = π .* prob
forward.z[:,n] = α₁
return α₁
else
# PRML(13.36)
αₙ = A' * forward( n - 1, p, X ) .* prob
forward.z[:,n] = αₙ
# HACK: ::VecOrMat{ Float64} となって強調色が出る
# return n == N ? forward.z : αₙ
return αₙ
end
end
mutable struct beta{R}
z::Matrix{R}
end
function (backward::beta)( n, p, X )
D, N = size(X)
# パラメータをアンパック
( ; K, A, π, μ, Σ ) = p
if n == N
# PRML(13.39)
βₙ = ones(K)
backward.z[:,n] = βₙ
return βₙ
else
# 潜在変数で条件づけられた出力関数の確率密度を計算
prob = [ pdf( MvNormal( μ[:,k], Σ[:,:,k] ), X[:,n+1] ) for k in 1:K ]
# PRML(13.38)
βₙ₊₁ = A * ( backward( n + 1, p, X ) .* prob )
backward.z[:,n] = βₙ₊₁
# HACK: ::VecOrMat{ Float64} となって強調色が出る でもα()*β()の形で書きたい気持ちだった
# return n == 1 ? backward.z : βₙ₊₁
return βₙ₊₁
end
end
# return Named Tuple
function init_params( m::HMM, X )
D, N = size(X)
K = m.n_state
# 潜在変数の初期値
A = fill( 1 / K, K, K )
π = fill( 1 / K, K )
# 多変数ガウスの初期値
kmeans_res = kmeans( X, K )
μ = kmeans_res.centers
Σ = begin
sig = zeros( D, D, K )
for k in 1:K
sig[:,:,k] = cov( X[:,assignments(kmeans_res) .== k]' )
end
sig
end
( K=K, A=A, π=π, μ=μ, Σ=Σ )
end
function init_Σ( D, K )
theta = 2.0 * pi / 12
A = reshape( [cos(theta), -sin(theta),
sin(theta), cos(theta)], 2, 2 )
Σ = zeros( D, D, K )
for k in 1:K
# HACK: 好きなサイズの逆行列を作りたい
Σ[:,:,k] = inv( A * inv( reshape( [1,0,0,10], 2, 2 ) ) * A' )
end
Σ
end
function poster_zₙzₙ₋₁(α, β, p, X)
D, N = size(X)
# パラメータをアンパック
( ; K, A, π, μ, Σ ) = p
znzn_1 = zeros( K, K, N - 1 )
for n in 2:N
prob = [ pdf( MvNormal( μ[:,k], Σ[:,:,k] ), X[:,n] ) for k in 1:K ]
# PRML (13.43)
znzn_1[:,:,n-1] = α[:,n-1] .* A .* β[:,n]' .* prob'
end
znzn_1 ./ sum( α[:,end] )
end
# PRML (13.18)
update_π( γ ) = γ[:,1] ./ sum(γ[:,1])
# PRML (13.19)
# HACK: sum関数でdimsを指定しただけでは3次元以降では次元が減らない?
update_transition_prob( zₙzₙ₋₁ ) = ( sum( zₙzₙ₋₁, dims=3 ) ./ sum( sum( zₙzₙ₋₁, dims=3 ), dims=2 ) )[:,:]
function update_emission_prob( γ, X, K )
D, N = size(X)
μ = zeros( D, K )
Σ = zeros( D, D, K )
for k in 1:K
# PRML (13.20)
μ[:,k] = sum( X .* γ[k,:]', dims=2 ) ./ sum( γ[k,:] )
squa = γ[k,1] .* ( X[:,1] - μ[:,k] )*( X[:,1] - μ[:,k] )'
for n in 2:N
squa += γ[k,n] .* ( X[:,n] - μ[:,k] )*( X[:,n] - μ[:,k] )'
end
# PRML (13.21)
Σ[:,:,k] = Symmetric( squa ./ sum( γ[k,:] ) )
end
μ, Σ
end
function sampling( rng, d, N, K, π₁, A )
X = zeros( K, N )
Z = zeros( K, N )
# パラメータπ₁からz₁を取得
zₙ = rand( rng, Multinomial( 1, π₁ ) )
for n in 1:N
Z[:,n] = zₙ
X[:,n] = rand( rng, d[argmax( zₙ )] )
# 遷移確立 Aᵢⱼ に応じて状態を遷移
zₙ = rand( rng, Multinomial( 1, A[argmax( zₙ ),:] ) )
end
X, Z
end
function Base.print(res::ResultsHMM)
display(res.π)
display(res.A)
display(res.μ)
display(res.Σ)
display(res.γ)
end
function test()
D, N, K = 2, 2, 2
# 潜在変数znの事後確率の実現値の配列のサイズは K * N
γ = [
0.1 0.2
0.9 0.8
]
@assert update_π(γ) == [ 0.1, 0.9 ]
# 潜在変数zn, zn-1の事後確率の実現値の配列のサイズは K * K * N
zₙzₙ₋₁ = [
0.1 0.2
0.2 0.5;;;
0.8 0.05
0.1 0.05
]
@assert update_transition_prob( zₙzₙ₋₁ ) == [
0.9/1.15 0.25/1.15
0.3/0.85 0.55/0.85
]
# μ, Σ = update_emission_prob( γ, X, K )
end
end # Q end
function plot_hmm(hmm, X, Z)
p1 = plot(hmm.γ[1,:], label="estimation", title="implement yourself")
plot!(p1, Z[1,:], label="obs")
# 初期化
model = HMM(
[0.9 0.1; 0.3 0.7],
[
MvNormal([0.,0.],[1.,1.]),
MvNormal([0.,0.],[1.,1.])
]
)
res, hist = fit_mle( model, X' )
prob = posteriors(res, X')
p2 = plot(prob[:,1], label="estimation", title="HMMBase.jl")
plot!(p2, Z[1,:], label="obs")
p3 = plot(hist.logtots, legend=false)
display(res)
plot(p1, p2, p3, layout=(3,1))
end
function main(rng)
D, K = 2, 2
N = 100
π₁ = [0.3, 0.7]
A = [
0.5 0.5
0.9 0.1
]
d = [
MvNormal( zeros(2), [1. 0.; 0. 1.] )
MvNormal( [1.,4.], [2. 0.; 0. 3.] )
]
X, Z = Q.sampling( rng, d, N, K, π₁, A )
hmm = Q.HMM( 2 )
res = Q.fit( hmm, X; maxiter=10^3 )
Q.print(res)
plot_hmm(res, X, Z)
end
Usage
using Random
const rng = Xoshiro(20220504)
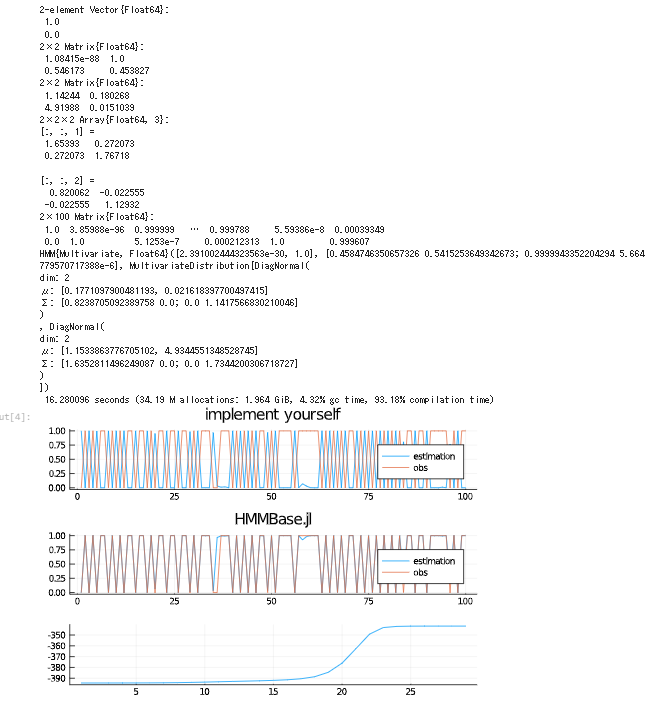
main(rng) # 出力は下記画像
プロットがひっくり返っていますが、ラベルを反転させればいいだけなので大した問題ではありません。