はじめに
まずはこちらの記事をご覧ください。見せかけの回帰の解説記事は時系列データへの回帰分析がめちゃくちゃおすすめです。著者は隼本でお馴染みの馬場真哉さん!!!ぜひご覧になってください。本記事でも様々なとこで引用させていただいています。
本記事を作成するにあたって検証した内容をGistあげてあります。使用したデータの値や、検定統計量も表示してあるので合わせてご覧ください。また、Gistでは、Julia+Rを使っております。検定部分はRのライブラリが非常に便利です。JuliaからRを使う例にもなっているので、ぜひ参考にしてみてください。
では本編スタートです!
見せかけの回帰
回帰分析を行ったときに、回帰係数のP値を確認すると思います。このP値は、回帰係数=0としたとき、回帰係数が0となる統計モデル内の確率を表しています。この確率が有意水準よりも小さい場合、帰無仮説(回帰係数=0)を棄却することになります。
その場合、得られたデータから作成した統計モデルにおいて、目的変数と説明変数になんらかの関係があるとみて差し支えないという結論になります。
「得られたデータから作成した統計モデルにおいて」とわざわざ強調して書いているのは、得られた結果が母集団分布を表しているわけではないからです。あくまで、有限のデータから我々が勝手に作った統計モデル内での話であるということを意識しておかなければなりません。
では、それらを踏まえた上でこちらをご覧ください。これはUSの個人消費支出をある変数Xで回帰分析したものです。但し、変数Xはどんな未来の値でも取得できると仮定します。
回帰係数のP値は$1e-79 << 0.01$ と有意水準1%としても明らかに有意であることを示しています。これが表すことは、知りたい未来時点での変数Xを持ってきて、回帰式に入れるだけで、個人消費支出の動向がわかるということです。
一旦、個人消費支出について補足しておきます。野村証券HPによると
米商務省が公表する、米国の家計が消費した財やサービスを集計した経済指標。英語名称はPCE(Personal Consumption Expenditures)。GDPの約7割を占める米国の個人消費支出はGDPの先行指標として注目される。また、個人消費支出のうち、変動の大きい食品とエネルギーを除いたコアPCEデフレーターは、米連邦準備理事会(FRB)がインフレ指標として重視することから、特に注目されている。
https://www.nomura.co.jp/terms/japan/ko/A02328.html
とあります。要はGDPの先行指標ということは景気の動向を先んじて知ることができるということです。例えば、景気が上向きであるとわかれば、個人では好景気によるインフレによって借入金の目減りが期待できます。つまりローンを組みやすいということですね。
ともあれ、景気の動向を知ることができるというのは大きなメリットがあるのです。
人にとってはいくらでも払うから、変数Xの情報が欲しい!となるかもしれませんね。では、この景気の行く末を占う変数Xの正体を教えます。変数Xは
$$
変数X : X_t = X_{t-1} + \epsilon_t \quad \epsilon_t ~ iid(0, \sigma)
$$
という式に従ってコンピュータを使って生成したランダムウォークです。これを聞いてまだお金を払いたいという方はいませんよね?
と、このように時系列データは単純に回帰分析を行うと、全く関係のない変数同士なのに、統計的には有意であるという結果が出てしまうことがあります。この現象のことを見せかけの回帰といいます。
定義6.1(見せかけの回帰)
単位根過程 $y_t$ を定数と $y_t$ と関係のない単位根過程 $x_t$ に回帰すると, $x_t$ と $y_t$ の間に有意な関係があり, 回帰の説明力が高いように見える現象は見せかけの回帰といわれる. 沖本[2010] 6章
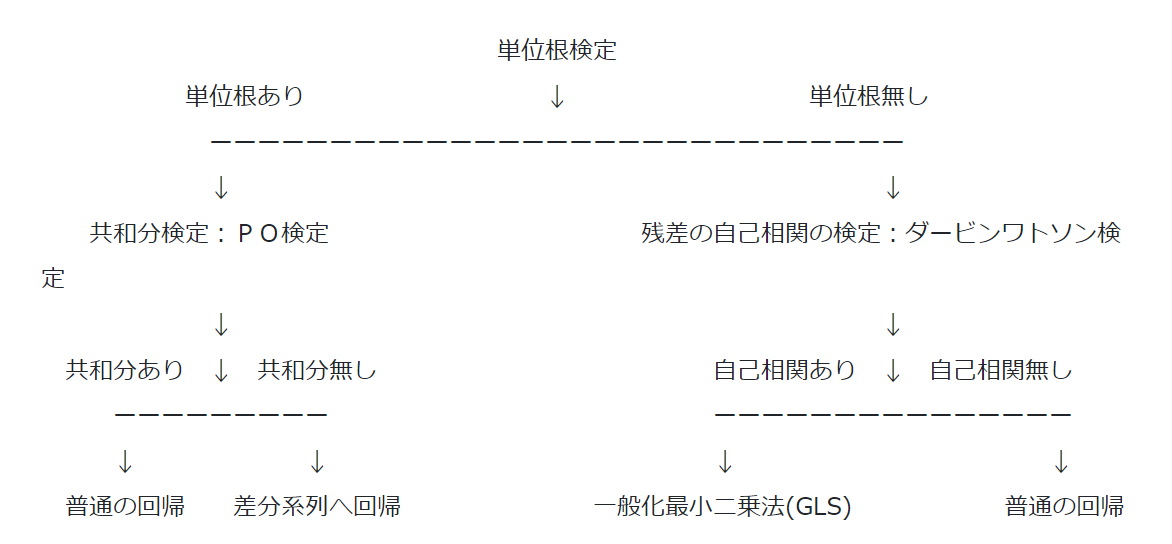
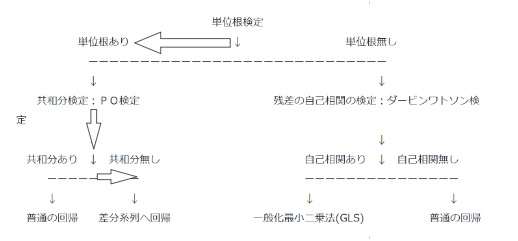
こんな見せかけの回帰を防ぐために回帰分析を行うためのデータチェックフローを馬場さんがブログで紹介してくださっています。以降これに従って、個人消費支出とランダムウォークに回帰分析を行っていきます。
データの読み込み
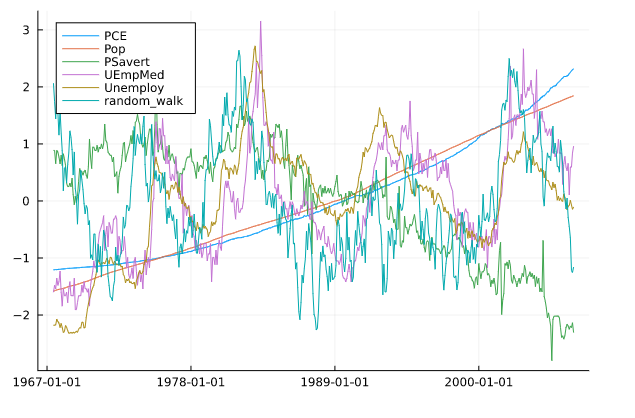
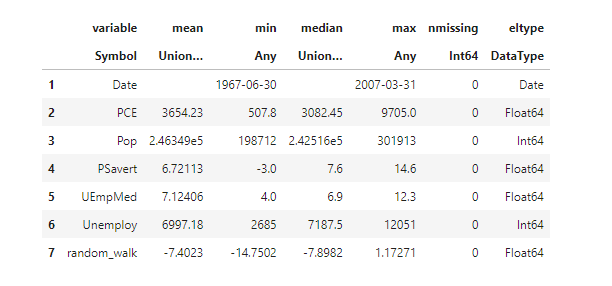
データはRデータセットのUS economic time seriesを使用します。特徴量間でデータの大きさが異なるので、標準化してまとめてプロットしました。本記事で取り扱うのはPCE(個人消費支出)だけです。PCE以外の特徴量に関してはGistをご覧ください。
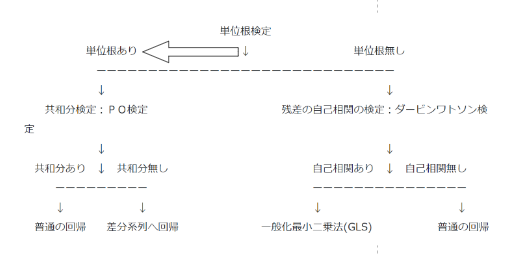
単位根検定を行う: Augmented Dickey-Fuller 検定
ではワークフローの第一段階です。単位根検定を行います。単位根については過去記事である単位根過程とトレンド定常過程の線形トレンドの違いをご覧ください。
今回はADF検定を使用して、特徴量が単位根であるかどうかをチェックしていきます。ADF検定とは帰無仮説にp次単位根AR過程であるとして検定を行います。画像は個人消費支出とランダムウォークに対してADF検定を行った結果のP値を示しています。
どちらも帰無仮説を棄却することはできないので、単位根過程ではないとは言えないことがわかります。
※PCEの統計量はワーニングが出ていたので、正確に0.99であるというわけではないことをご了承ください。


共和分検定を行う: Phillips-Ouliaris 検定
続いては共和分検定です。共和分とは何ぞやということなのですが、馬場さんのブログによると、
単位根を持つデータ同士に、ある係数をかけてから合計すると、たまに「単位根がなくなる」ことがあります。 そんな関係のことを「共和分」と呼びます。
データが共和分を持っている場合は、たとえ単位根があったとしても、そのまま回帰分析を実行して支障ありません。
時系列データへの回帰分析より引用
とあります。つまり単位根同士を回帰させると必ずしも、見せかけの回帰にならないよということです。見せかけの回帰ではないのに単位根を解消しようと差分を取ってしまうと、本来利用可能な情報まで失われてしまうことになります。
では実際にPCEとランダムウォークに対してPO検定を行っていきます。PO検定は共和分が存在しない(残差が単位根を持つ)、を帰無仮説に検定を行います。
tstatが検定統計量でcval5は有意水準5%でのモデル内の統計量です。$tstat < cval5$ なので帰無仮説を棄却することができません。よって共和分は存在する(残差が単位根を持たない)とは言えないとなります。
すなわち、系列に差分を取って分析を行っても、失われる情報が少ないと考えることができます。
差分系列に対して回帰分析を行う
では実際に差分を取った場合に回帰係数のP値がどうなるのか見てみましょう。まずは原系列に対して回帰分析を行ったときの結果を再掲します。
次に差分を取った場合です。
回帰係数のP値が大きくなったのがわかります。ただ注意してほしいのは、回帰係数のP値が大きいからと言って、変数間に関係があるとは言えないということです。これは検定は片方の行動に対してしか自信を持つことができないのと同じことです。すなわち、P値が小さい場合、関係がないとはいえるが、その逆は何とも言えないということです。
終わりに
時系列データは特に統計モデルの基本的な前提条件をぶっ飛ばしがちな特性があります。例えば、データは独立して生成されているというのが通例ですが、時系列データは過去のデータに依存していることが多いです。
単純に回帰分析を行ってP値が小さい→有意だ!ではいけません。実際には上記のように考慮しなければいけない点がたくさんあるのです。