分数次差分とは
本記事はファイナンス機械学習を参考に分数次差分の実装とその解説を行います。ファイナンス機械学習 第5章 分数次差分をとった特徴量 P97~
分数次差分とは、その名の通り差分の取り方を正の実数まで拡張したものです。例えば、表現が正しくないのであくまでイメージとして考えてほしいのですが、時系列データにおいて1期先のデータと差分を取っていたものを、1/2期先差分または1.2期先差分をとれるように拡張するのが今回のお話です。今後、単なる差分のことを整数次差分といいます。
分数次差分の何がうれしいかといいますと、原系列の情報をなるべく残したまま定常な系列に変えることができるのです。もともと金融時系列データは低いS/N比を取ることが知られています。加えて整数次差分を取ってしまうと、系列データの平均値の推移の情報(ファイナンス機械学習ではメモリー)が消えてしまいます。これはただでさえ小さいシグナルを余計に小さくしてしまうことを表しています。
ファイナンス機械学習では、整数次差分はどんな系列データに対しても情報を削除しすぎていることを指摘しており、3/5以下で差分を取ることで定常性は得られるといっています。
手法解説
バックシフトオペレーター(ラグオペレーターともいう)ってなに?
手法解説に入る前に皆さん、バックシフトオペレーター(ラグオペレーターともいう)をご存知でしょうか?論文とかでよく使われる書き方なので、ファイナンス機械学習でもバックシフトオペレーターを使っています。難しいことはありません、以下のルールにしたがって変数をシフトさせていくだけです。バックシフトオペレーターを $B$ とすると、
B^{k}X_{t} = X_{t-k}
ここで $X_{t}$ は系列データです。例えば、バックシフトオペレーターを使うとARモデル(AutoRegressive Model)も次のように表せます。
\begin{align}
AR(p) : y_{t} &= c + \Sigma^{P}_{p=1} \phi_{p} y_{t-p} + noise \\
&⇔ (1 - \phi_{1}B - \phi_{2}B^{2} - ... - \phi_{p}B^{p} )y_{t} = c + noise \\
&⇔ \phi_{p}(B)y_{t} = c + noise \\
\end{align}
ここで、$\phi_{p}(B)=(1 - \phi_{1}B - \phi_{2}B^{2} - ... - \phi_{p}B^{p} )$ は $B$ の $p$ 次多項式を表しています。ARモデルについてもっと詳しく知りたいよという方は以下のリンクがおすすめです。上記のARモデルの表現も以下のリンクを参考にしました。また、ARモデルに付随して単位根過程を学びたい方は、私が過去に「単位根過程とトレンド定常過程の線形トレンドの違い」という記事を書いたのでそちらもご覧ください。
話がそれましたが以上がバックシフトオペレーターについての簡単な説明になります。
分数次差分の定式化
バックシフトオペレーター $B$ を使って、1次の整数次差分は $(1 - B)X_{t} = X_{t} - X_{t-1}$ と表すことができます。2次の整数次差分は $(1 - B)^{2}X_{t} = X_{t} -2 X_{t-1} + X_{t-2}$ と表すことができます。これらを利用して指数を任意の正の実数に拡張すれば分数次差分が定義できますね。すなわち分数次差分は二項級数展開で定義されます。
\begin{align}
(1 - B)^{d} &= \Sigma^{\infty}_{k=0} \begin{pmatrix}
d \\
k
\end{pmatrix} (-B)^{k} \\
&= 1 -dB + \frac{d(d-1)}{2!}B^{2} - \frac{d(d-1)(d-2)}{3!}B^{3} + ...
\end{align}
すなわち分数次差分の係数は次のように表せます。
\omega = \bigg[ 1, -d , \frac{d(d-1)}{2!}B^{2}, - \frac{d(d-1)(d-2)}{3!}B^{3}, ... , (-1)^{k}\Pi^{k-1}_{i=0} \frac{d-i}{k!}, ... \bigg]
これを見ると $d=1$ の時は $\omega = [1, -1]$ となり1次の整数次差分と同じになることがわかります。
分数次差分の計算
分数次差分は逐次計算が可能です。
\begin{align}
\omega_{0} &= 1 \\
\omega_{k} &= -\omega_{k-1} \frac{d-k-1}{k}
\end{align}
function getWeights( d, size )
w = ones(size)
for k=1:size-1
w[k+1] = - w[k]*( d - k + 1 ) / k
end
w
end
d次分数次差分のウェイトの様子
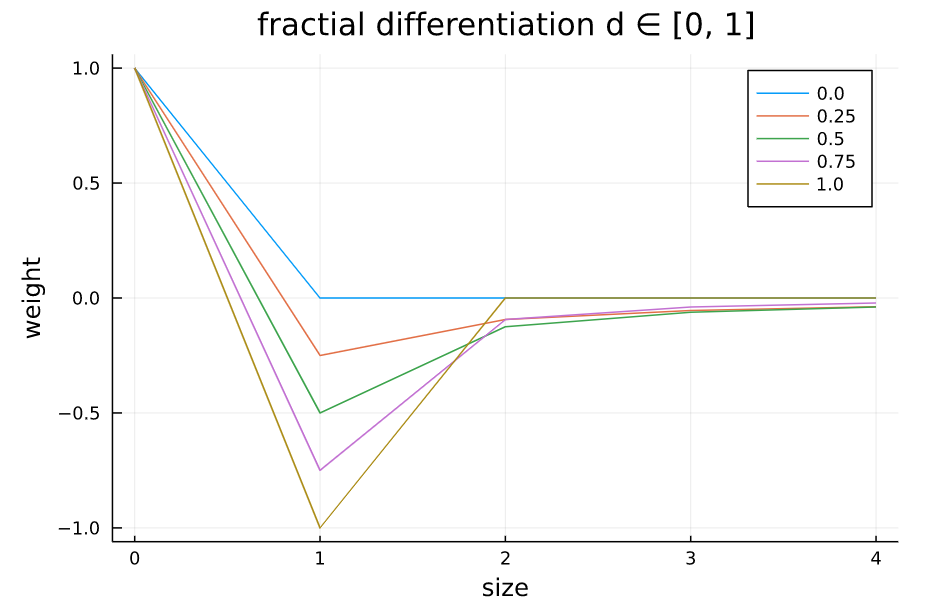
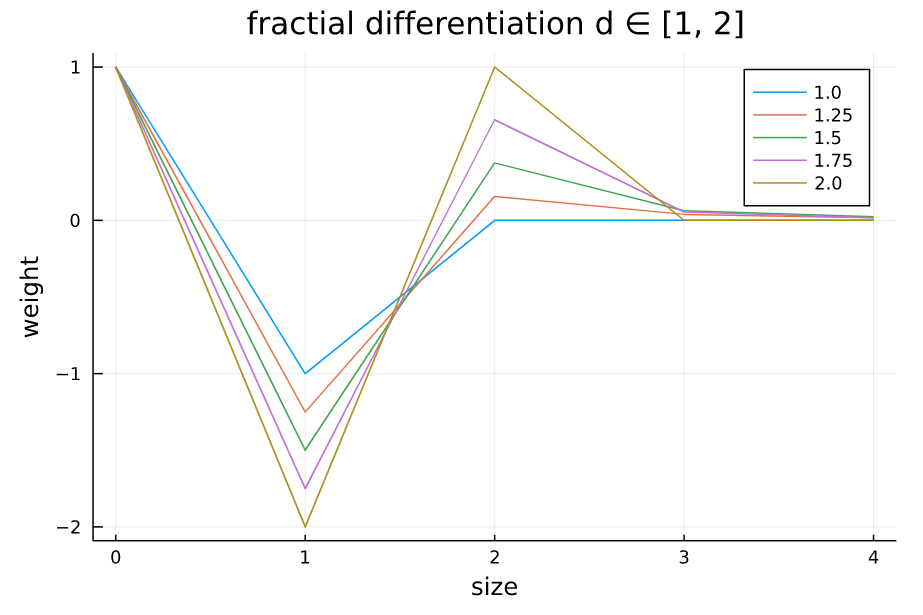
次のグラフは横軸のkの値( $\omega_{0}, \omega_{1}, ..., \omega_{k}$ ということ)を増やしたとき、縦軸をウェイトの値がどのように変化するか、様々な $d$ の値で計算たものです。 例えば、$d=1$ にすると、 $k \geq 1$ ですべてのウェイトの係数は $0$ になります。これは原系列と同じであることを示しています。
また、ウェイトは減衰傾向であることがグラフから読み取れます。ではどこまでをウェイトとして使用すればいいでしょうか?実際に系列データにウェイトを適用させようとすると悩みますよね。
ファイナンス機械学習では、二種類の方法を紹介しています。「拡大ウィンドウ」と「固定幅ウィンドウ」です。大きな違いとしては、前者はウェイトの長さが変化するのに対して、後者はウェイトの長さは固定になります。この長さが変化するというのがよくわからないと思いますが、詳しい説明は次の章に引き継ぎます。
上記のプロットを作成するために使ったコード
using Plots
x = 0:0.25:1
labels = string.(x')
plot(
0:length(x)-1,
getWeights.(x, 5),
labels=labels,
title="fractial differentiation d ∈ [0, 1]",
xlabel="size",
ylabel="weight"
)
using Plots
x = 1:0.25:2
labels = string.(x')
plot(
0:length(x)-1,
getWeights.(x, 5),
labels=labels,
title="fractial differentiation d ∈ [1, 2]",
xlabel="size",
ylabel="weight"
)
拡大ウィンドウによる分数次差分
拡大ウィンドウはウェイトの長さが変化するということがイメージできれば、難しくありません。まず大前提として拡大ウィンドウのウェイトは系列の長さと同じ分だけの長さを持ちます。次のような系列 $X$ とウェイト $\omega$ について考えてみましょう。
\begin{align}
X &= \bigg[ X_{1}, X_{2}, ... , X_{10} \bigg] \\
\omega &= \bigg[ \omega_{1}, \omega_{2}, ... , \omega_{10} \bigg]
\end{align}
系列は $X_{10}$ 側がより最新のデータとします。ここで、$X_{10}$ に対してd次の分数次差分を取るとき次のように計算できます。
\begin{align}
X'_{10} &= \Sigma_{k=0}^{9} \omega_{k+1} X_{10-k}
\end{align}
$X_{9}$ に対しては、
\begin{align}
X'_{9} &= \Sigma_{k=0}^{8} \omega_{k+1} X_{10-k}
\end{align}
$\omega$ の数に注目してください。$X_{9}$ について計算するとき、$\omega_{10}$ は計算に現れませんね。ウェイトの長さが変わるとはこのことを指しています。
さて、このまま計算していくと、$X_{10}$ と $X_{1}$ の情報が異なってしまいますね。( $X_{1}$ のときのウェイトは $\omega_{1} = 1$ つまり情報が減っていない )
そこで、拡大ウィンドウでは相対損失ウェイトを定め、それを超えるようなウェイトの削除は行わないようにします。上記の計算でわかるようにウェイトは数値が小さいほうから消えていきます。つまり $X_{10}', X_{9}',...$ をどこまで計算できるか、とも言い換えられます。
ファイナンス機械学習では相対損失ウェイトを
\lambda = \frac{\Sigma^{T}_{j=T-l} |\omega_{j}|}
{\Sigma^{T-1}_{i=0} |\omega_{i}|}
と定めています。
余談ですが、個人的には分子が少し変だと思ってて、このまま書き下すと $\omega_{T}$ が出てくるのですが、分母の $\omega$ は最大でも $\omega_{T-1}$ にしかなりません。つまり $\omega_{T}$ があると、ウェイトの長さが系列の長さを超えている気がするのですよね、、、
なので私は、相対損失ウェイトは次のように書き換えました。
\lambda = \frac{\Sigma^{T-1}_{j=T-l-1} |\omega_{j}|}
{\Sigma^{T-1}_{i=0} |\omega_{i}|}
【閑話休題】
ファイナンス機械学習では拡大ウィンドウのPythonでの実装が載っています。私はJuliaを書くのが好きなのでJuliaで書き直しました。
# 拡大ウィンドウ法
"""
fracDiff( series, d, thres=.01 )
d ∈ R, d ≧ 0
thres ∈ [0, 1]
FIXME:thres=1の時,戻り値のベクトルの先頭に0が入ってしまう
"""
function fracDiff( series, d, thres=.01 )
L = length(series)
# 最長の系列に対してウェイトを計算する
w = getWeights( d, L )
# 閾値に基づいて, スキップするウェイトを計算する
w_ = cumsum( abs.(w[end:-1:1]) )
w_ ./= w_[end]
skip = length(w_[w_ .> thres])
# データにウェイトを適用
X = zeros( length( skip:L ) )
for n in skip:L
X[n-skip+1] += w[begin:n]' * series[begin:n][end:-1:1]
end
X
end
using LinearAlgebra
x = normalize(X);
xx = fracDiff( x, 0.5 );
L = length(x) - length(xx)
xx = vcat( (missing for i in 1:L)..., xx );
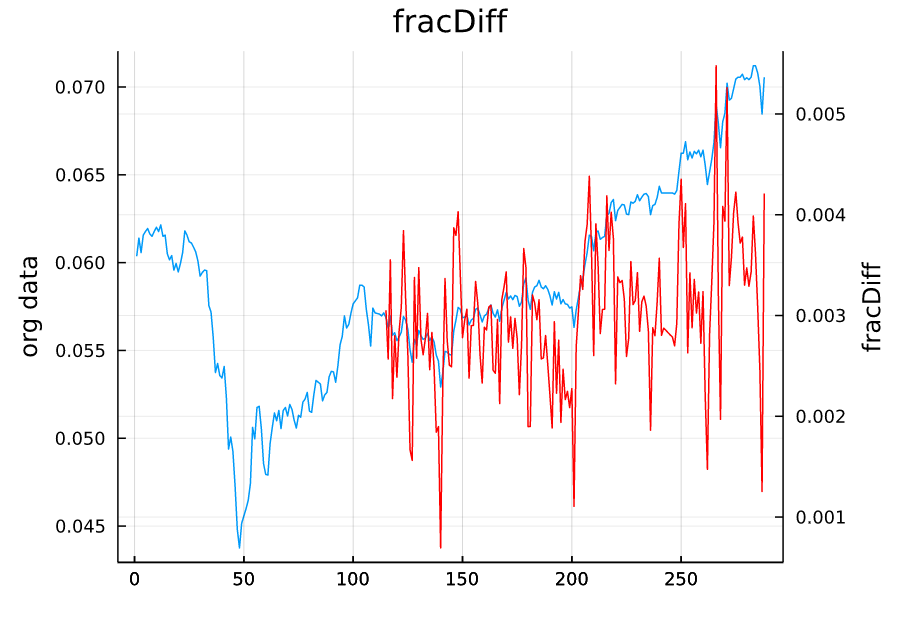
plot(x, right_margin=20mm, title="fracDiff", labels=false, ylabel="org data")
plot!(twinx(), xx, color=:red, labels=false, ylabel="fracDiff")
固定幅ウィンドウによる分数次差分
固定幅ウィンドウは各ウェイトに対して、閾値を比較します。閾値を超える部分のウェイトについてはすべて捨て去り、残りのウェイトを使用します。
拡大ウィンドウと同様の例で考えてみます。
\begin{align}
X &= \bigg[ X_{1}, X_{2}, ... , X_{10} \bigg] \\
\omega &= \bigg[ \omega_{1}, \omega_{2}, ... , \omega_{10} \bigg]
\end{align}
ここで閾値を $\tau$ として、ウェイトと閾値の関係が次のようになったとします。
\begin{align}
|\omega_{3}| \leq \tau, \quad
|\omega_{4}| \geq \tau \\
\omega_{k}' = \bigg \{ \begin{array}{ll}
\omega_{k} & ( k \leq 3) \\
0 & ( k \gt 3)
\end{array}
\end{align}
この時ウェイトは $\omega = [ \omega_{0}, ... , \omega_{3}]$ となります。拡大ウィンドウと異なる点は、ウェイトの各係数と閾値を比べていることです。また系列データに適用するときにウェイトの長さが変わらないのも特徴の一つといえます。
# 固定幅ウインドウ
function getWeights_FFD( d, thres )
w, k = [1.], 1
while true
w_ = - w[k]*( d - k + 1 ) / k
abs( w_ ) < thres && break
push!(w, w_)
k+=1
end
w
end
"""
fracDiff_FFD( series, d, thres=1e-5 )
d ∈ R, d ≧ 0
thres ∈ [0, 1]
"""
function fracDiff_FFD( series, d, thres=.01 )
L = length(series)
w = getWeights_FFD( d, thres )
width = length(w)
width >= L && error("(weight, series) = ($width, $L)
ウェイトの長さが系列の長さを超えています. thresの大きさを調整してください.")
X = zeros(L-width+1)
for n in 1:L-width+1
X[n] += w' * series[n:width+n-1][end:-1:1]
end
X
end
using LinearAlgebra
x = normalize(X);
xx = fracDiff_FFD( x, 0.5 );
L = length(x) - length(xx)
xx = vcat( (missing for i in 1:L)..., xx );
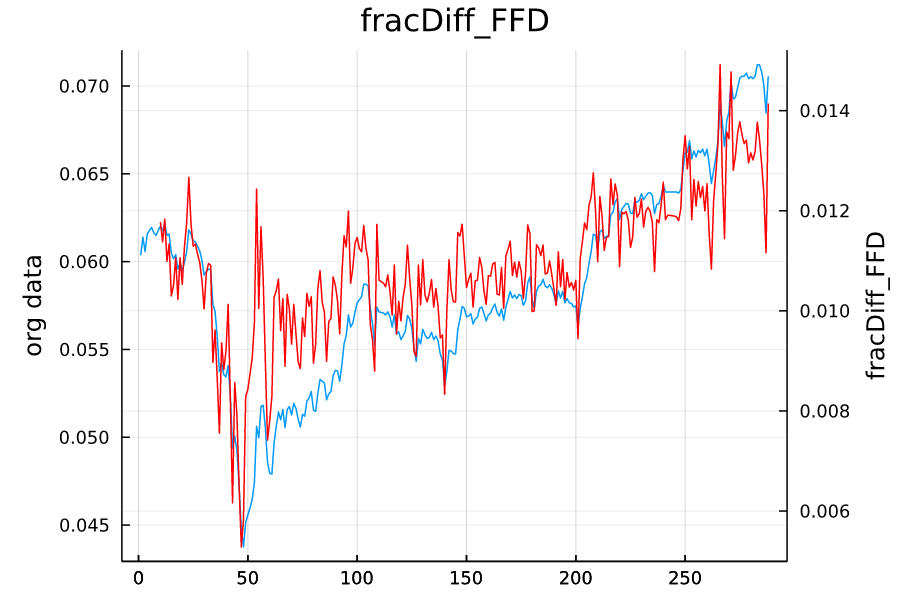
plot(x, right_margin=20mm, title="fracDiff_FFD", labels=false, ylabel="org data")
plot!(twinx(), xx, color=:red, labels=false, ylabel="fracDiff_FFD")
分数次差分がどれほど有用であるか
これまで私たちは、分数次差分の定式化及び系列データに対してどのように分数次差分を適用するのかということを見てきました。最後の章では実際に分数次差分が整数次差分と比べてどれほど原系列の情報を保った、定常なデータに変換できるのかということを見ていきます。
今回使用するデータはNEXT FUNDS TOPIX連動型上場投信です。データは株式投資メモ 株価DBからダウンロードしました。期間は2020-01-06~2021-06-22です。
※ちなみにここに来るまでにいくつか時系列データをプロットしているのですが、全く同じデータを使用しています。
まず、この系列データに対して $d$ 次の分数次差分をとります。今回は固定幅ウィンドウを使用して分数次差分を取ります。また、分数次差分をとった系列データを以後、加工済み系列データと呼称することにします。
加工済み系列データに対してADF検定を行い、ADF検定統計量を保存しておきます。
ADF検定とは簡単に言うと、系列データが単位根過程つまり非定常データであるかどうかを判定する検定です。つまり、ADF検定を使って、系列データがどんな $d$ の値で定常になるのかを観察しようということです。
検定には、設定しなければいけないことがあるのですが、今回はファイナンス機械学習と同じ設定で行いたいと思います。
次に、原系列と加工済み系列データの相関係数を計算します。相関係数が高ければ、元々の系列データの情報を多く保持しているとみなします。
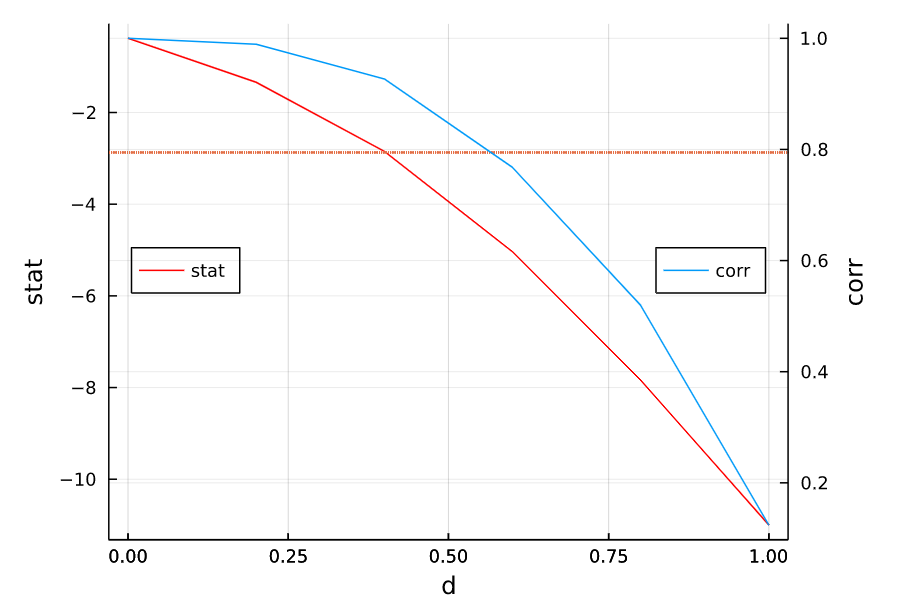
さて、実際に計算した結果をプロットしたものがこちらです。
赤いドットの線はADF検定統計量95%信頼水準の臨界値で $-2.87163$ です。グラフをよく見ると、$d=0.403$ 付近で系列データがADF検定の帰無仮説を棄却していることがわかります。このときの原系列と加工済み系列データの相関係数は0.8弱とかなりの高水準であることがわかります。整数次差分を取ると相関係数の値は $0.124$ になります。
以上の結果により系列データに対して整数次差分を取るのは、情報を余計に削除していることがわかります。
using Plots
using Plots.PlotMeasures
using Statistics
using HypothesisTests
function plot_cor_stat(X, d_ran, symbol=:none, lags=1)
r = zeros(length(d_ran))
st = zeros(length(d_ran))
for d = 1:length(d_ran)
X_ = fracDiff_FFD(X, d_ran[d])
len = length(X) - length(X_) + 1
r[d] = cor(X_, X[len:end])
st[d] = ADFTest(X_, symbol, lags).stat
end
r, st
end
d = (0:.2:1)
r, st = plot_cor_stat(X, d, :constant)
plot(d, st, labels="stat", color=:red, xlabel="d", ylabel="stat", legend=:left, right_margin=20mm)
plot!(twinx(), z, r, labels="corr", ylabel="corr", legend=:right)
hline!(x->-2.87163, line=:dot, label=false)