コイン投げの最大連続数から極値統計について考えてみたメモ

はじめに

Qiitaで以下の記事を読んでなるほどなーと思ったので、Pythonを使って感覚と実際の数値について考えていたら、極値統計だと気づいて実際にプロットしてみたメモ

コイン投げ100回試行を1回したときの結果

まずは視覚的に確認するコードを書いてみました（内包表記だらけなのは単なる好み）。
なるほど確かに結構連続する数は多いもんなんだなーと感じます。

[ソースコード]

import random
import itertools

coin = [('○' if random.random() >= 0.5 else '●') for x in range(100)]
text = ''.join([f'{str(coin[x])}\n' if (x + 1) % 10 == 0 else f'{str(coin[x])}' for x in range(100)])

print(text)
print(f'○：{text.count("○")}回, ●：{text.count("●")}回\n')

sequ = [list(g) for k, g in itertools.groupby(coin)]
freq = [len(sequ[x]) for x in range(len(sequ))]

for x in range(1, 21):
    print(f'同じ面が {x:02} 回続いて出た回数：{freq.count(x):02}回, 出現割合：約{(freq.count(x)/len(freq)*100):.2f}%')

[出力結果]

出力結果

○●●●●○○○●○
●○●○○○●●●●
●●●●○●●●○○
○●●●●●●○●●
○●○○●○○○●○
○●●●○●●○○○
○○●○○●●○●●
●○●●●○○○○○
○○○●●○○●○●
●○○●●●●●●○

○：46回, ●：54回

同じ面が 01 回続いて出た回数：19回, 出現割合：約44.19%
同じ面が 02 回続いて出た回数：10回, 出現割合：約23.26%
同じ面が 03 回続いて出た回数：08回, 出現割合：約18.60%
同じ面が 04 回続いて出た回数：01回, 出現割合：約2.33%
同じ面が 05 回続いて出た回数：01回, 出現割合：約2.33%
同じ面が 06 回続いて出た回数：02回, 出現割合：約4.65%
同じ面が 07 回続いて出た回数：00回, 出現割合：約0.00%
同じ面が 08 回続いて出た回数：02回, 出現割合：約4.65%
同じ面が 09 回続いて出た回数：00回, 出現割合：約0.00%
同じ面が 10 回続いて出た回数：00回, 出現割合：約0.00%
同じ面が 11 回続いて出た回数：00回, 出現割合：約0.00%
同じ面が 12 回続いて出た回数：00回, 出現割合：約0.00%
同じ面が 13 回続いて出た回数：00回, 出現割合：約0.00%
同じ面が 14 回続いて出た回数：00回, 出現割合：約0.00%
同じ面が 15 回続いて出た回数：00回, 出現割合：約0.00%
同じ面が 16 回続いて出た回数：00回, 出現割合：約0.00%
同じ面が 17 回続いて出た回数：00回, 出現割合：約0.00%
同じ面が 18 回続いて出た回数：00回, 出現割合：約0.00%
同じ面が 19 回続いて出た回数：00回, 出現割合：約0.00%
同じ面が 20 回続いて出た回数：00回, 出現割合：約0.00%

コイン投げ100回試行を100万回したときの結果

次にコイン投げ100回試行を100万回繰り返して、各回の最大連続数が何回か集計してみます。
適当に書いたのもあって出力に25秒くらいかかりました。

[ソースコード]

import random
import itertools
from tqdm import tqdm

maxi = []
for n in tqdm(range(1000000)):
    coin = [('○' if random.random() >= 0.5 else '●') for x in range(100)]
    sequ = [list(g) for k, g in itertools.groupby(coin)]
    freq = [len(sequ[x]) for x in range(len(sequ))]
    maxi.append(max(freq))

x = []
y = []
z = []
for t in tqdm(range(1, 31)):
    x.append(t)
    y.append(maxi.count(t))
    z.append((maxi.count(t)/len(maxi)*100))

import pandas as pd

df = pd.DataFrame(data={'最大連続数': x, '出現回数[回]': y, '出現割合[%]': z})

[出力結果] 最大連続数とその出現回数および出現割合

最大連続数	出現回数[回]	出現割合[%]
1	0	0%
2	0	0%
3	284	0.0284%
4	27783	2.7783%
5	165010	16.5010%
6	264678	26.4678%
7	227197	22.7197%
8	146818	14.6818%
9	81514	8.1514%
10	43195	4.3195%
11	21640	2.1640%
12	10969	1.0969%
13	5538	0.5538%
14	2655	0.2655%
15	1377	0.1377%
16	684	0.0684%
17	312	0.0312%
18	176	0.0176%
19	89	0.0089%
20	44	0.0044%
21	14	0.0014%
22	12	0.0012%
23	7	0.0007%
24	2	0.0002%
25	0	0%
26	1	0.0001%
27	1	0.0001%
28	0	0%
29	0	0%
30	0	0%

結果、100万回繰り返すと最大連続数が3回というのも0.03%程度の確率で発生するので、一番最初の画像もあり得ないわけではなさそうですが、出現割合0.03%では現実的な試行回数で出てくるものとは言い難いようです。

また5～8回が10％超えなので、現実的にはほぼこの範囲になりそうです。

面白いのは最大連続数27回などかなり連続数が多いものも低確率ですが存在する点です。1/1,000,000の確率で出てくるものの存在を直感的には理解し難いですし、実際に確認できるのはプログラムの良い点です。

極値分布

と、ここまでやってみて、最大値の集計してるから、これ極値分布じゃんと気づいたので方向修正

極値分布やその数式については以下のリンク先などを参照していただくとして、ここではプログラムでサクッと結果が得られることから、実際に計算させてみました。
（ちなみに私自身そこまで数学の知識があるわけではないので、数学的に正しくない、計算手法が間違っている、という可能性も大いにありますのでそのつもりで読んでください）

また極値統計は実学的には以下のような形で使われるものになります。

最大連続数の算出

上記のコードを少し変更して最大連続数を100回、1000回、1万回、10万回、100万回試行した結果を算出して、それぞれの最大連続数の最大値を出すと以下のようになります。

試行回数が1桁増えると最大連続数が4程度増えていく結果となりました。

試行回数	100回	1000回	1万回	10万回	100万回
最大連続数	12	16	20	24	28

ソースコード

import pandas as pd
import random
import itertools

x = []
maxi = []
for n in range(100000): #ここの数値を変えて出力
    coin = [('○' if random.random() >= 0.5 else '●') for i in range(100)]
    sequ = [list(g) for k, g in itertools.groupby(coin)]
    freq = [len(sequ[i]) for i in range(len(sequ))]
    x.append(n + 1)
    maxi.append(max(freq))

df = pd.DataFrame(data={'x': x, 'y': maxi})
df.to_csv('maxi.csv')

二重指数確率紙へのプロット

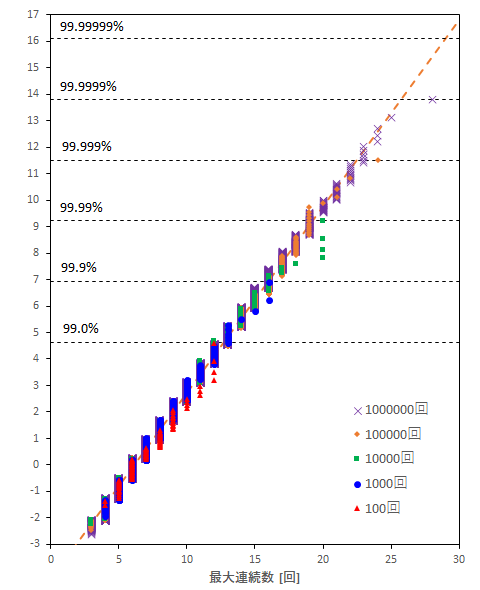
上記の試行結果を二重指数確率紙へプロットした結果が以下のようになります。

※Pythonで補助線やら凡例やらを正確にいじれる自信がなかったので、Excelでグラフ化しています。100万行のデータをグラフで扱うと流石にフリーズしかけました。

ほぼ直線となり、極値統計での整理ができる結果となっているようです。
また試行回数がそのまま最大値の出現確率になるので、試行回数の桁が増えるごとにx軸の最大値が増えていき、理論通りだと確認できます。

ただ100万回試行時の最大連続数28というのは、このプロットからすると少し外れる値のようです。

また計算時間的に確認していませんが、極値統計上は1000万回試行すれば最大連続数が30程度までが出現することになりそうです。

試行回数が少ない側のプロット

極値統計で試行回数が多い側で最大値は予測することはできそうですが、それを予測するためのデータ数がどの程度少なくても良いのかを考えてみました。

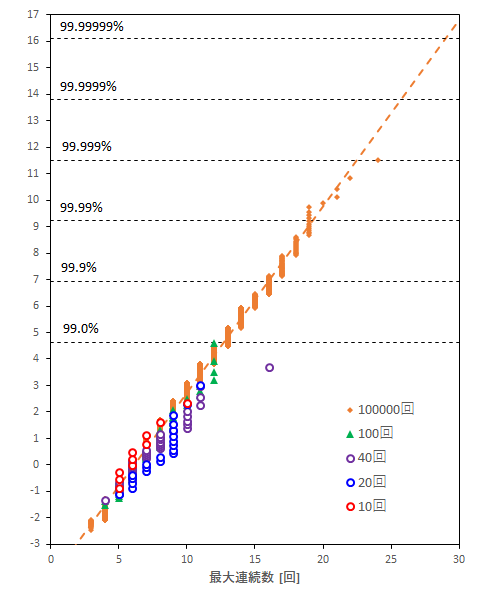
以下のグラフでは10回、20回、40回、100回、10万回のプロットを載せています。

その結果、10回は10万回のプロットと重なっていますが、20回、40回などは多少ズレている状態となっています。
これは10回がよいのではなく、たまたまそうなっただけで、試行回数が少ない場合は突発的なデータで直線性が崩れやすい状態にあるように思えます（40回繰り返したなかに、1/1000回の確率で出る最大連続数が含まれる可能性もあり得るため）

実際に極値統計を適用する際にはあまりデータ数が多くない場合もありますが、データ数による影響も加味して予測する必要がありそうです。

さいごに

仕事で極値統計を使ったことがあったのですが、あまり感覚的に納得できていなかった部分もあったのを、意図せず実際に計算してみる機会ができて理解が深まったように思います。

いろいろな分野に触れてみるのは面白いですね。