Databricksでhyperoptを用いてハイパーパラメーターチューニングをやってみる

Parallelize hyperparameter tuning with scikit-learn and MLflow | Databricks on AWSのサンプルノートブックをウォークスルーします。これまでは、ノートブックを実行したことしかなかったので、自分で疑問と思った部分も調査しました。

Hyperoptのコンセプトに関してはこちらをご覧ください。

翻訳したサンプルノートブックはこちらにあります。

注意
Databricks機械学習ランタイム11.3MLで動作確認しています。

Hyperoptの分散処理と自動化されたMLflowトラッキング

HyperoptはハイパーパラメーターチューニングのためのPythonライブラリです。Databricks機械学習ランタイムには、最適化かつ強化されたバージョンのHyperopt、分散チューニング向けの自動MLflowトラッキング、SparkTrialsクラスが含まれています。

このノートブックでは、シングルマシン向けのPython機械学習アルゴリズムのハイパーパラメーターチューニングをどのようにスケールアップし、MLflowを用いて結果をトラッキングするのかを説明します。パート1では、シングルマシンのHyperoptワークフローを作成します。パート2では、Sparkクラスターでワークフローの計算処理を分散させるためにSparkTrialsクラスの使用法を学びます。

必要なパッケージのインポートとデータセットのロード

Python

from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score
from sklearn.svm import SVC

from hyperopt import fmin, tpe, hp, SparkTrials, STATUS_OK, Trials

# Databricks機械学習ランタイムを実行している場合、`mlflow`はインストール済みですので以下の行をスキップすることができます。
import mlflow

Python

# scikit-learnからirisデータセットをロード
iris = iris = load_iris()
X = iris.data
y = iris.target

パート1. シングルマシンのHyperoptワークフロー

Hyperoptのワークフローにおけるステップは以下の通りです:

1. 最小化する関数を定義
2. ハイパーパラメーターに対する探索空間を定義
3. 探索アルゴリズムを選択
4. Hyperoptのfmin()を用いてチューニングアルゴリズムを実行

詳細はHyperopt documentationをご覧ください。

最小化する関数の定義

このサンプルでは、サポートベクトルマシンの分類器を使用します。ここでのゴールは、正則化パラメーターCの最適な値を見つけ出すことです。

Hyperoptワークフローのコードの大部分は目的関数です。このサンプルでは、support vector classifier from scikit-learnを用いています。

Python

def objective(C):
    # サポートベクトル分類モデルの作成
    clf = SVC(C)
    
    # モデルのパフォーマンスを比較するために交差検証の精度を使用
    accuracy = cross_val_score(clf, X, y).mean()
    
    # Hyperoptは目的関数を最小化しようとします。高い精度の値は優れたモデルであることを意味するので、負の精度を返却するようにしないといけません。
    return {'loss': -accuracy, 'status': STATUS_OK}

ハイパーパラメーターの探索空間の定義

探索空間とパラメーターの表現の定義の詳細についてはHyperopt docsをご覧下さい。

疑問
hyperoptの探索空間はどう定義するのだろう？グリッドサーチとの違いは？

グリッドサーチでは、探索するパラメーターの組み合わせを指定します。これらのパラメーターは離散値となりますが、hyperoptでは正規分布など確率分布を考慮して柔軟にハイパーパラメーターを探索することができます。探索するパラメーターの確率分布に前提を置くことで、それに応じた探索空間を定義することができます。

hyperoptの最適化アルゴリズムで認識される確率論的な表現には以下のものがあります:

• hp.choice(label, options)

  選択肢の一つを返却し、listかtubleである必要があります。選択肢の要素を[ネストされた]確率論的表現にすることも可能です。この場合、選択肢のいくかにおける確率論的な選択肢は条件付きパラメータとなります。

• hp.randint(label, upper)

  範囲[0, upper)のランダムな整数値を返却します。この分布のセマンティクスは、ロス関数において、離れた整数値と比較して、近隣の整数値との間に相関がないというものです。これは、例えばランダムのシードを記述する際に適切な分布です。ロス関数が近隣の整数値とより相関している場合には、quniform, qloguniform, qnormalやqlognormalのように「quantized(量子化された)」連続分布を使用しなくてはならないかも知れません。

• hp.uniform(label, low, high)

  • lowとhighの間にある均等な値を返却します。
  • 最適化を行う際、この変数は2面性の間隔に制約を受けます。

• hp.quniform(label, low, high, q)

  • round(uniform(low, high) / q) * q のような値を返却します。
  • 目的変数が依然として「スムーズ」な離散値で上限値、下限値がある場合に適しています。

• hp.loguniform(label, low, high)

  • 戻り値の対数値が均一に分散するように、exp(uniform(low, high))から導かれる値を返却します。
  • 最適化の際、この変数は間隔[exp(low), exp(high)]の制約を受けます。

• hp.qloguniform(label, low, high, q)

  • round(exp(uniform(low, high)) / q) * qのような値を返却します。
  • 目的変数が「スムーズ」で値のサイズに応じてよりスムーズになるような離散値で上限値、下限値の制約を受ける場合に適しています。

• hp.normal(label, mu, sigma)

  • 平均値の mu と標準偏差の sigma の正規分布の実数を返却します。最適化の際は制約のない変数となります。

• hp.qnormal(label, mu, sigma, q)

  • round(normal(mu, sigma) / q) * qのような値を返却します。
  • mu 周辺の値を取り、基本的に未制限の離散値の場合に適しています。

• hp.lognormal(label, mu, sigma)

  • 戻り値の対数が正規分布になるように、exp(normal(mu, sigma))から導かれた値を返却します。最適化の際、この変数は正の数であるという制約を受けます。

• hp.qlognormal(label, mu, sigma, q)

  • round(exp(normal(mu, sigma)) / q) * qのような値を返却します。
  • 目的変数が「スムーズ」で値のサイズに応じてよりスムーズになるような離散値で、一方向でのみ制約を受ける場合に適しています。

均等な分布からハイパーパラメーターを選択するのであればhp.uniform、選択肢からパラメーターを選択するのであればhp.choice、正規分布から選択するのであればhp.normalを使うというイメージです。これらは組み合わせることも可能です。

以下の例では、ハイパーパラメーターが対数正規分布であると仮定して探索空間を定義しています。

Python

# 対数正規分布
search_space = hp.lognormal('C', 0, 1.0)

探索空間の可視化

疑問
定義した探索空間は具体的にどうなっているのか？

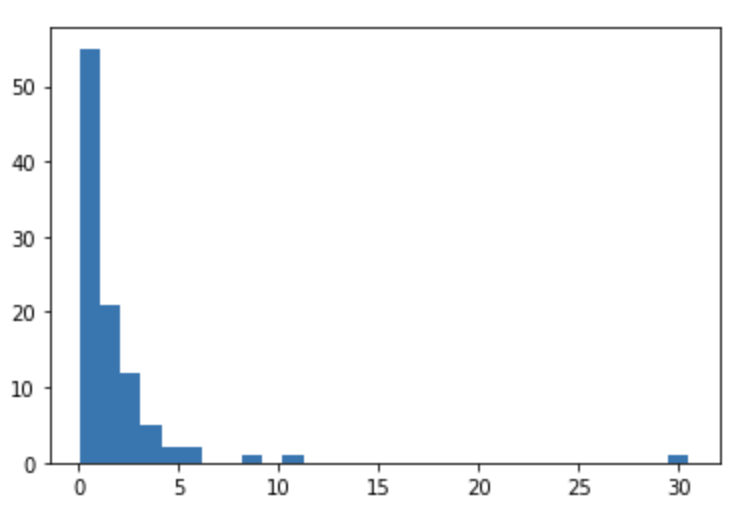
上で定義した探索空間がどのようになっているのかを確認するために、探索空間からデータポイントを抽出します。サンプリングの方法は以下で説明されています。

Defining search spaces - Hyperopt Documentation

探索空間からパラメーターをサンプリングして可視化してみます。

Python

import hyperopt.pyll.stochastic
import matplotlib.pyplot as plt

values = []

# 100ポイントをサンプリング
for i in range(100):
  sample = hyperopt.pyll.stochastic.sample(search_space)
  #print("sample:", sample)
  values.append(sample)
  
plt.hist(values, density=False, bins=30)  # density=False would make counts

対数正規分布になっていることがわかります。

探索アルゴリズムの選択

主な選択肢は以下の2つです:

• hyperopt.tpe.suggest: Tree of Parzen Estimators、過去の結果に基づいて探索する新たなハイパーパラメーターの設定を繰り返しかつ適合的に選択するベイジアンアプローチ
• hyperopt.rand.suggest: ランダムサーチ、探索空間のサンプリングを行う非適合型のアプローチ

Python

algo = tpe.suggest

Hyperoptのfmin()を用いてチューニングアルゴリズムを実行

テストすべきハイパーパラメーター空間の最大ポイント数、すなわち、フィッテイングして評価するモデルの最大数をmax_evalsで設定します。

Python

argmin = fmin(fn=objective, space=search_space, algo=algo, max_evals=16)

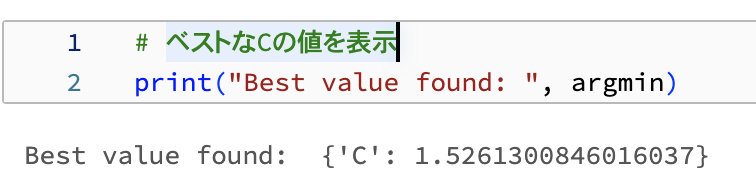
ベストなCの値を表示します。

Python

# ベストなCの値を表示
print("Best value found: ", argmin)

パート2. Apache SparkとMLflowを用いた分散チューニング

チューニングを分散するには、fmin()の引数にSparkTrialsと呼ばれるTrialsクラスを追加します。

SparkTrialsは2つのオプションの引数を受け取ります:

• parallelism: 同時にフィット、評価するモデルの数。デフォルトは利用可能なSparkタスクのスロット数です。
• timeout: fmin()を実行できる最大時間(秒数)です。デフォルトは時間制限はありません。

このサンプルでは、Cmdで定義された非常にシンプルな目的関数を使用します。この場合、関数はクイックに実行され、Sparkジョブの起動のオーバーヘッドが計算時間の大部分を占めるので、分散処理の場合は計算処理はさらに時間がかかります。典型的な現実的なユースケースでは、目的関数はより複雑となり、分散させるためにSparkTrailsを用いることで、シングルマシンのチューニングよりも計算処理が高速になります。

デフォルトで自動MLflowトラッキングが有効化されています。使用するには、サンプルで示しているようにfmin()を呼び出す前にmlflow.start_run()を呼び出してください。

Python

from hyperopt import SparkTrials

Python

spark_trials = SparkTrials()

with mlflow.start_run():
  argmin = fmin(
    fn=objective,
    space=search_space,
    algo=algo,
    max_evals=16,
    trials=spark_trials)

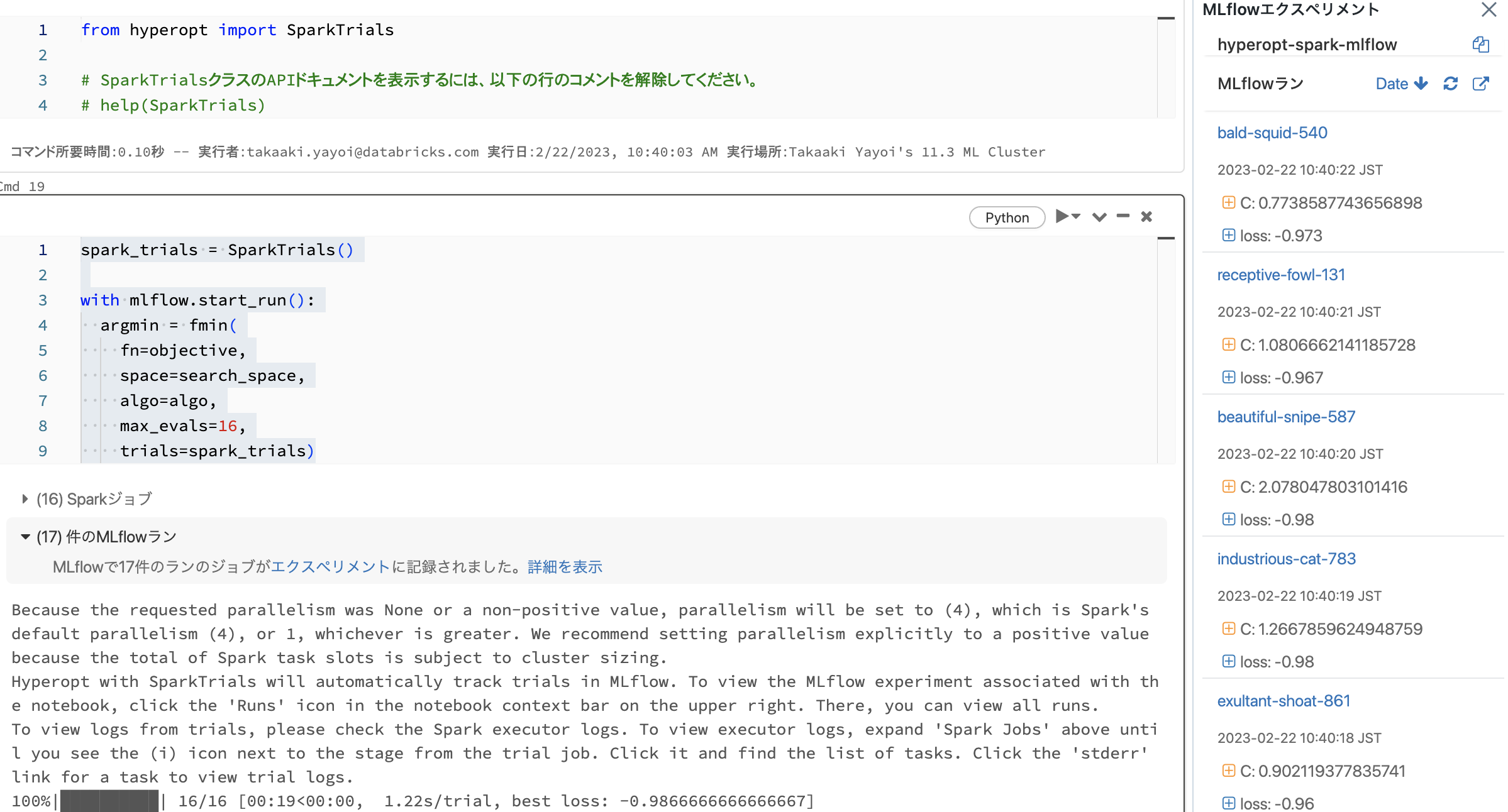
並列でハイパーパラメーターチューニングを行った結果生成されるモデルはすべてMLflowによってトラッキングされます。

Python

# ベストなCの値を表示
print("Best value found: ", argmin)

チャートビューの活用

ノートブックに関連づけられているMLflowエクスペリメントを参照するには、ノートブック右側にあるフラスコアイコンをクリックします。そこでは、すべてのMLflowランを参照することができます。MLflow UIからランを参照するには、MLflowランの右端にある右上向き矢印のアイコンをクリックします。

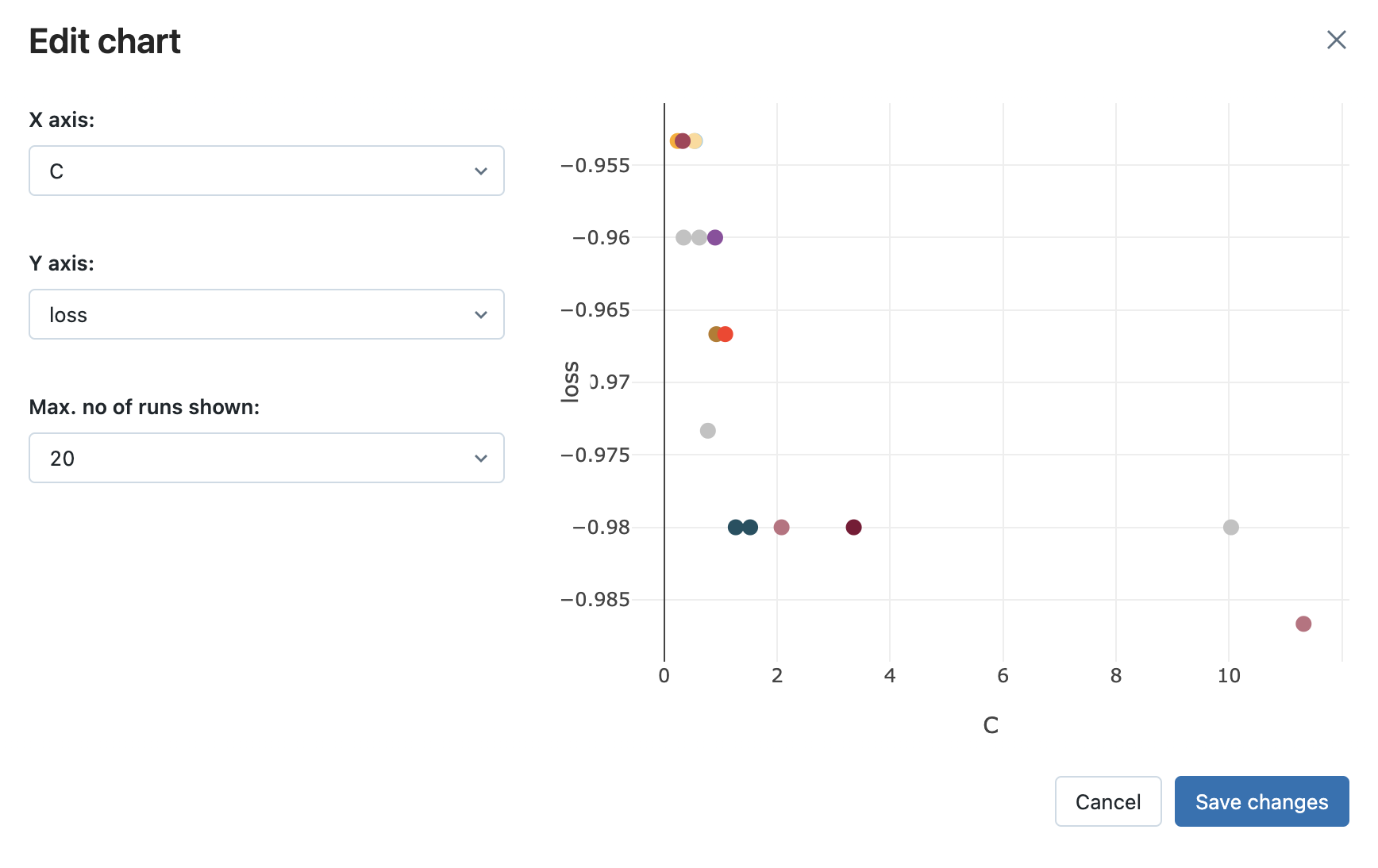
最近導入されたチャートビューを用いることでクイックにパフォーマンスを確認することができます。

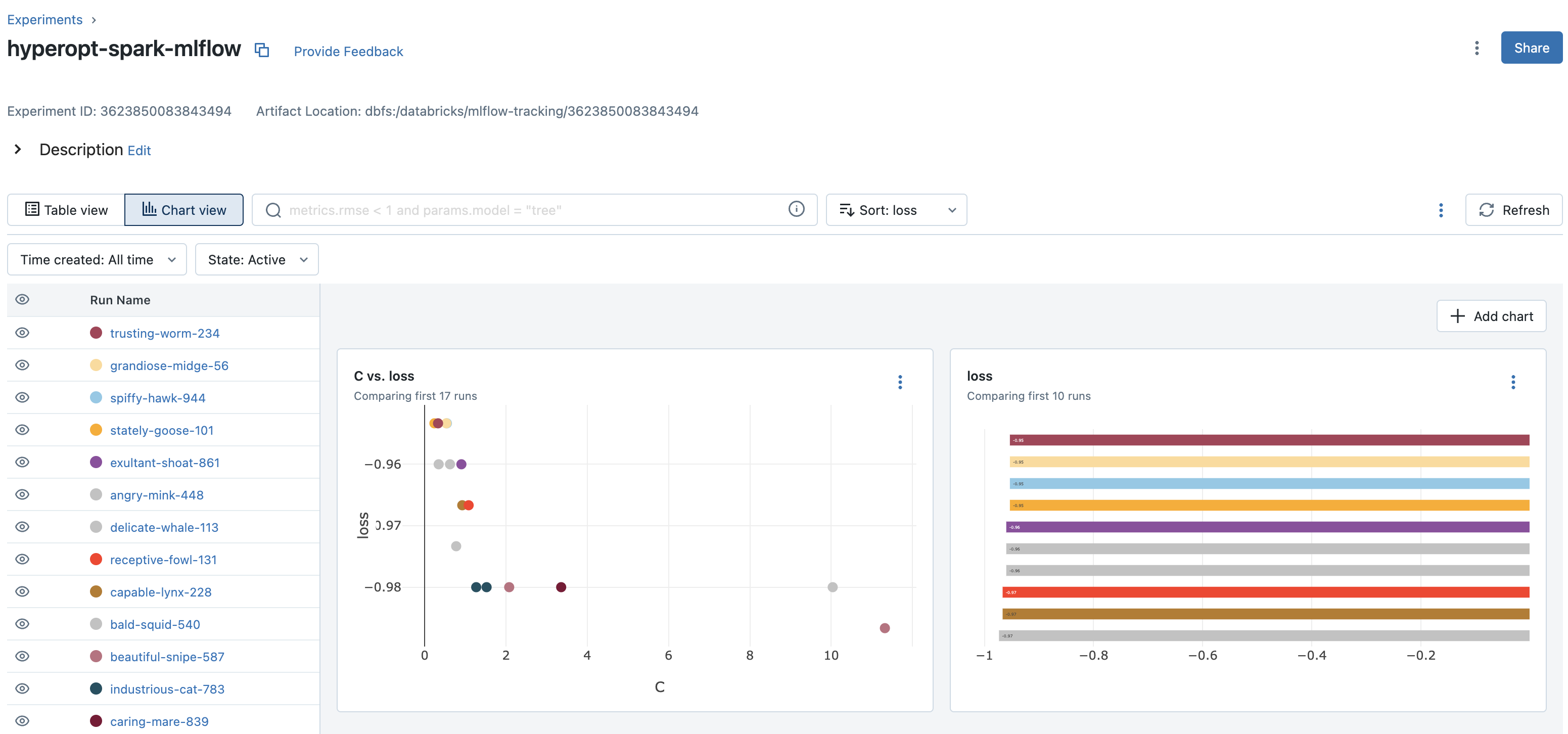
まとめ

探索空間の定義の柔軟性、並列ハイパーパラメーターチューニングによる処理の高速化を活用できるhyperopt + Sparkの組み合わせを是非お試しください！

Databricks 無料トライアル

Databricks 無料トライアル