はじめに
実験データを直線で近似して評価する,ってよくありますよね(回帰分析).
直線で近似するためには,なんらかの指標に沿って良い感じの線を引くわけですが,その指標は色々あるわけです.データと直線の最大の誤差を小さくしたい($L_{\infty}$最適化),とか誤差の二乗和($L_2$)を小さくしたいとか,誤差の絶対値の和($L_1$)とか.
この記事では,直線近似の時に用いる評価関数を$L_1, L_2, L_{\infty}$と変えた時,直線はどんな感じに推定されるのか,pythonの凸最適化ツールのcvxpyを使って計算します.
cvxpyとは:pythonで凸最適化問題を解くためのツールです.凸最適化問題はいろいろと考慮しないといけないことが多かったりするのですが(問題の変形とか),その辺をパパっと解決してくれる優れものです.
一番簡単で,よく使われるのが$L_2$ノルム最適化(最小二乗)ですが,こいつはデータに外れ値が入ってきたときに挙動がおかしくなります(外れ値の影響が二乗で効いてくるため).
$L_1$最適化は外れ値に強いと言われますが,実際どの程度ロバストなんだろう,と疑問に思ったので調べてみました.
とりあえず個人的に思っている$L_p$ノルム最適化のイメージ
- $L_2$:導出と実装が超楽,観測ノイズが正規分布の時の最尤推定.
- $L_1$:実装がめんどうだけど,凸最適化問題だからツールさえあれば楽.外れ値に対してロバスト.
- $L_{\infty}$:とにかく大きい誤差が嫌いな時に使う.$H_{\infty}$制御で出てくる.
つまり
統計学の分野では,「観測ノイズは正規分布だと仮定して最尤推定直線を求める」,とかよく耳にします.
得られたデータを直線$y=ax+b$で近似した時に,最も確からしいパラメータ$a,b$を求める,ということです.
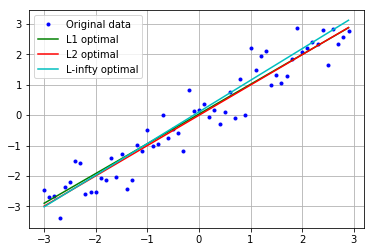
上の図で言うと,青い点が得られたデータ,赤い直線が近似直線です.
観測ノイズが平均ゼロの正規分布に従う場合は,最尤推定(確率的に最も良い感じの推定)=「推定誤差の$L_2$ノルムを最小にする推定」であることが知られています.しかし実際には「観測ノイズが平均ゼロの正規分布に従う場合」の仮定が当てはまらないことも多いので,誤差の指標は別に$L_2$ノルムに限らなくてもいいわけです.上でも述べましたが,$L_2$ノルム最適化は特に外れ値に対して推定結果が強く影響を受けます.
ここでは回帰に用いる評価関数の指標を$L_1, L_2, L_{\infty}$ノルムとして,それぞれの性能を比較してみたいと思います.
ノルムとは
ノルムとは「距離」とか「大きさ」のことです.
例えば,
a=[1,2,3]\\
b=[0, 0, 5]
という2つのベクトル$a,b$があったとします.この$a$と$b$ってどっちが大きいですか?と言われると困りますよね.
最大値的には$b$の方が大きいけど,全要素の和は$a$の方が大きいし...となります.
ここで出てくるのがノルムです.ノルムはこれらのベクトルに対する「大きさ」を定義するものなので,ノルムを使えばどちらが大きいかに対して明確に答えることができます.
ノルムにはいろいろな種類があり,その用途に応じて使い分けられます.
ベクトル$x=[x_1,x_2,\cdots,x_n]$に対する一般的なノルムをいくつか下に書きます.
- $L_1$ノルム
L_1=\sum_{i=1}^n |x_i|
- $L_2$ノルム
L_2=\left[\sum_{i=1}^n |x_i|^2\right]^{\frac{1}{2}}
- $L_{\infty}$ノルム
L_{\infty}=\max_i |x_i|
- $L_0$ノルム
L_0=\sum_{i=1}^n\delta(x_i),\quad \delta(x_i)=
\begin{cases}
1\ (x_i \neq 0)\\
0\ (x_i=0)
\end{cases}
こんな感じですね.ノルムは,ノルムが満たすべき性質があって(例えば必ずノルムは正値とか),それを満たせばどんな形でもいいです.なので,自分たちで勝手にノルムを定義してしまってもokです.
ここで述べたノルムは$L_p$ノルムと呼ばれて,次の一般形で書かれます.
L_p=\left[\sum_{i=1}^n |x_i|^p\right]^{\frac{1}{p}}={}^{\frac{1}{p}}\sqrt{|x_1|^p+|x_2|^p+\cdots+|x_n|^p}
なので,$L_3$ノルムとか$L_{100}$ノルムもありですね.(厳密には上で書いた$L_0$ノルムは定義上ノルムではなく,単なる$L_p$ノルムに対する$p\rightarrow 0$の極限です.ですが,結構有用らしいので覚えておいて損はないです)
で,$a$と$b$どちらが大きいかという話ですが,ベクトルに対する$L_p$ノルムを$\parallel\cdot\parallel_p$と書けば,
\parallel a \parallel_1=|1|+|2|+|3|=6\\
\parallel b \parallel_1=|0|+|0|+|5|=5
なので,「$L_1$ノルムの意味では」$a$の方が大きいということになります.一方で,
\parallel a \parallel_2=\sqrt{|1|^2+|2|^2+|3|^2}=\sqrt{14}\\
\parallel b \parallel_2=\sqrt{|0|^2+|0|^2+|5|^2}=\sqrt{25}
となるので,「$L_2$ノルムの意味では」逆に$b$の方が大きいですね.
このように,基本的にベクトルの大小関係とか大きさは,「どのノルムで大きさを評価するか」に依存します.
データの回帰を行う場合は,一般的にたくさんのデータを取り扱います.データ数が$n$個だとすれば,近似直線を決めた時,その1つ1つのデータに対して近似誤差が計算できます.この近似誤差が小さいほど近似直線の精度が良いということになりますが,近似誤差は$n$次元ベクトルで表されるので,その近似誤差の大きさは評価するノルムに依存します.なので,最適な近似直線といっても「$L_1$ノルムの意味で近似誤差を最小にする直線」とか,「$L_2$ノルムの意味で近似誤差を最小にする直線」など,いろいろあるわけです.今回はそれらを実際に計算して比較してみます.
ちなみに,行列にもそれに対応するノルムがあって,フロベニウスノルムとかいろいろなノルムがいます.(行列ノルム)
推定法の説明
問題を以下のように設定します.
何らかの入出力関係$(y\in R, x\in R^k)$があったときに,その関係性を以下の線形近似で求めたいとします.
y=A^Tx, \quad A\in R^k
ベクトル$A$が推定したいパラメータです.
ただし,観測データ$y$にはノイズが乗っているため,観測データ$y$に対してこの等式は成り立ちません.誤差も考慮して式を書くと
y=A^Tx+e
となります.$n$個の観測データに対してこの式を適用すれば
\begin{bmatrix}
y(1)\\y(2)\\ \vdots \\ y(n)
\end{bmatrix}
=
\begin{bmatrix}
x_1(1) & x_2(1) & \cdots & x_k(1) \\
x_1(2) & x_2(2) & \cdots & x_k(2) \\
& & \vdots & \\
x_1(n) & x_2(n) & \cdots & x_k(n) \\
\end{bmatrix}
\begin{bmatrix}
A_1 \\ A_2 \\ \vdots \\ A_k
\end{bmatrix}
+
\begin{bmatrix}
e(1) \\ e(2) \\ \vdots \\ e(n)
\end{bmatrix}
まとめて
Y=XA+E
とします(表記の関係上$A^Tx$と$XA$で$x$と$A$順番が変わってます).この誤差ベクトル$E$を$L_1, L_2, L_{\infty}$ノルムに対して最小化するようなパラメータ$A$をそれぞれ求めてみます.
L2最適化(最小二乗推定)
一番簡単な$L_2$ノルム最適化から話します.誤差の$L_2$ノルムは$e(1)^2+e(2)^2+\cdots$なので,ベクトルの内積を使って$E^TE$で書けます.$Y=XA+E$を使って式変形をすると
|| E || _2 = E^TE=(Y-XA)^T(Y-XA)=Y^TY-Y^TXA-A^TX^TY+A^TX^TXA
になります.この誤差はパラメータ$A$に対して下に凸の二次式になっているので,$A$で微分して0になるところが最小値になります.
結果,$L_2$最適推定値は
\hat A_{L2}=(X^TX)^{-1}X^TY
となります.逆行列の計算だけで解が求まるので,最も簡単でよく使われる方法の一つです.
ちなみに,大規模な行列演算において逆行列を求めるのは計算誤差が大きいので,$L_2$最適推定値は
(X^TX)A=X^TY
の解,として書かれることもあります.この場合は逆行列を使うことなく,別の方法(例えば共役勾配法)で上の方程式を解いて推定値$\hat A$を求めます.
pythonでは下のように最小二乗推定はnumpyに入っている関数で実行できます.
import numpy as np
A_hat = np.linalg.lstsq(X, y)[0]
簡単ですね.$X$とか$y$とかの定義は最後に載せたコードを確認してください.
L1最適化
次は$L_1$最適化です.$L_2$と比べて$L_1$は少しめんどくさいですが,$L_1$最適化は凸最適化問題というジャンルに属しているので,比較的解きやすい部類になります.
評価関数は$|e(1)|+|e(2)|+\cdots= || E || _1$になります.
この最適化問題は,$Y=XA+E$を使って定式化すると,以下のようになります.
\min_A \quad ||Y-XA||_1
これはつまり
\min_A \quad \sum_{i=1}^n |y(i)-Ax(i)|
こう.このままだと絶対値が入っていて凸最適化問題として解けないので,これを凸最適化問題の形式に変形します.
まず,新たなベクトル変数$t\in R^n$を用意して
\min_{A,\ t} \quad \sum_{i=1}^n t_i,\\
{\rm subject\ to}\quad |y(i)-Ax(i)|<t(i),\quad \forall i
こうなる.変数$t$が追加されていますが,最適化問題の意味は何も変わってません(i番目の要素を(i)って書いたの見にくかったな...)
絶対値を外すと
\min_{A,\ t} \quad \sum_{i=1}^n t_i,\\
{\rm subject\ to}\quad -t(i)<y(i)-Ax(i)<t(i),\quad \forall i
となり,凸最適化問題に落とせます.
これで$L_1$最適化問題が凸最適化で解けることが分かりました.ちなみにcvxpyを使うと,上で述べたようなややこしい変換を挟むことなく,下のコードのように$L_1$最適化が実行できます.
import numpy as np
import cvxpy as cv
A = cv.Variable(n)
objective = cv.Minimize(cv.norm(y - X * A, 1))
constraints = []
prob = cv.Problem(objective, constraints)
result = prob.solve()
objectiveが目的関数で,誤差 $Y-XA$ の$L_1$ノルムを最小化してくれ,と設定するだけで問題を解いてくれます.いやー,簡単ですね.(詳しくは後で出てくるコードを確認)
L無限大ノルム最適化
$L_{\infty}$ノルムは$\max$と同じなので,イメージは簡単です.この問題も実は凸最適化問題に落とし込めるので,高速で解くことが可能です.
$L_{\infty}$最適化問題を定式化すると,
\min_A \quad || Y-XA||_{\infty}
これはつまり
\min_A \quad \max |Y-XA|
こう.これを$L_1$最適化と同様のテクニックで凸最適化問題に落とし込みます.今回はスカラ変数$t\in R$を使って,変形すると
\min_{A,\ t} \quad t\\
{\rm subject\ to}\quad -t<y(i)-Ax(i)<t,\quad \forall i
こんな感じ(頭いい...).
これで,凸最適化ツールを使って問題が解けます.(もちろん,変数が少ない場合はグリッドリサーチみたいにしてパラメータを最適化してもいいですが,凸最適化の手法を使った方がおそらく圧倒的に高速です)
cvxpyで書くと,コードはこんな感じ.
import numpy as np
import cvxpy as cv
A = cv.Variable(n)
objective = cv.Minimize(cv.norm(y - X * A, np.inf))
constraints = []
prob = cv.Problem(objective, constraints)
result = prob.solve()
変換とか挟むことなく,いきなり$L_{\infty}$ノルムの最小化を指定して,最適化問題を解かせることができます.(詳しくは後で出てくるコードを確認)
コードと結果
pythonの凸最適化ツールであるcvxpyを使って回帰問題を解きます.
※詳しく調べてませんが,python3.6とcvxpyの相性が悪いらしくインストールで若干詰まったので,pythonのバージョンを下げて対応しました.https://github.com/cvxgrp/cvxpy/issues/332
なお,$L_2$最適化はnumpyに実装されていたので,cvxpyは使わずに書いてます.
# -*- coding: utf-8 -*-
import numpy as np
import cvxpy as cv
import matplotlib.pyplot as plt
# data generation: y = a*x + b + w(0, sigma2)
a = 1
b = 0
n = 2 # parameter size
theta = np.array([a, b]) # parameter vector
sigma2 = 0.5 # noise variance
x = np.arange(-3, 3, 0.1)
X = np.zeros((len(x), 2), float)
X[:,0] = x
X[:,1] = 1
w = np.random.normal(0.0, sigma2, len(x))
y = X.dot(theta) + w
# y[50] = 100 # outlier
# y[20] = 100 # outlier
# y[5] = 100 # outlier
plt.plot(x, y, 'b.', label='Original data')
# L1 optimization
A = cv.Variable(n)
objective = cv.Minimize(cv.norm(y - X * A, 1))
constraints = []
prob = cv.Problem(objective, constraints)
result = prob.solve()
A_hat = A.value
print("L1 optimization result: ", A_hat)
y_hat = X.dot(A_hat)
plt.plot(x, y_hat, 'g', label='L1 optimal')
# L2 optimization
A_hat = np.linalg.lstsq(X, y)[0]
y_hat = X.dot(A_hat)
print("L2 optimization result: ", A_hat)
plt.plot(x, y_hat, 'r', label='L2 optimal')
# L-infty optimization
A = cv.Variable(n)
objective = cv.Minimize(cv.norm(y - X * A, np.inf))
constraints = []
prob = cv.Problem(objective, constraints)
result = prob.solve()
A_hat = A.value
print("L-infty optimization result: ", A_hat)
y_hat = X.dot(A_hat)
plt.plot(x, y_hat, 'c', label='L-infty optimal')
plt.legend()
plt.grid()
ノイズ入りのデータを作って,
外れ値を一か所入れて,
線形回帰の最適化問題を$L_1,\ L_2,\ L_{\infty}$の順で解いてます.
結果はこんな感じ
外れ値が y[50]=10 のとき($L_{\infty}$は一撃で瀕死)
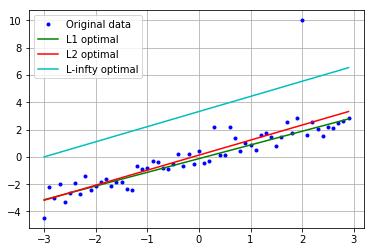
外れ値が y[50]=100 のとき(そろそろ$L_2$も限界)
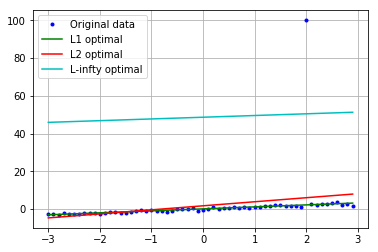
これから,$L_{1}$,$L_{2}$,$L_{\infty}$の順で,外れ値に対してロバストであることが分かります.
まあそれは想定通りなんですが,$L_1$が想像以上にしっかりと推定ができていて,驚いています.
さらに外れ値を3箇所に与えて,意地悪してみます.
y[50] = 100 # outlier
y[20] = 100 # outlier
y[5] = 100 # outlier
結果はこんな感じ(こうかはばつぐんだ!$L_2$は倒れた!)
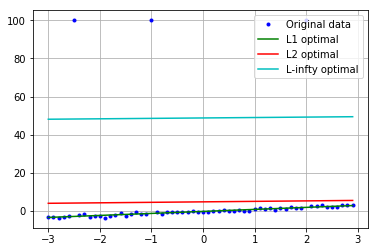
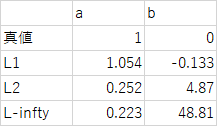
ちなみにこの時のパラメータは
y=ax+b+w(0,\sigma^2),\quad a=1,\ b=0, \ \sigma^2=0.5
で,推定結果が
($L_1$おまえすごい...)
よく考えたら,データにどれだけ外れ値が入ってきても,外れ値側に動かした分だけ外れ値じゃない方の誤差が増えるわけで,$L_1$ノルム的にはその比率は1:1なんだから,データ数が多い方に合わせに行くのか..
ってことはどれだけ外れ値が入ってきても,少数派でさえあればいいのか..?
多項式回帰とかでも同じ感じなのかな?気になる...
参考リンク
- Lp space(wiki):誰が読むん,ってくらいまとめられてる
- cvxpyの使い方(MyEnigmaさん):参考にさせていただきました
- 凸最適化pdf(UCLA):応用例とか載ってて面白い