微分方程式の数値計算ソルバー(特にode45)について解説します。
・微分方程式ってどうやって計算してるんだろう?
・とりあえずmatlabでode45と書いたら微分方程式が解けた。けど、こいつ中で何やってるんだろう?
・ルンゲクッタ?ああ、聞いたことあるな
そんな人向けです。
ode45って何?
matlabに出てくる微分方程式を解くためのソルバーの名前で、odeは常微分方程式「ordinary differential equation」の略です。
matlabのサイトによると「関数 ode45 は、Dormand-Princean の陽的 Runge-Kutta (4,5) 公式に基づきます。」と書いてありますが、知識が無いとなかなかにツラいですね。
いきなり結論を書くと、ode45はルンゲクッタの4次と5次の手法の結果を比較して、動的にステップサイズを変更することによって、精度と計算コストを両立して微分方程式を数値計算するための方法です。
以下は細々とした詳細。
微分方程式のあれこれ
数値的に解く、とは
ここで扱うのは常微分方程式(微分する変数が1つ)です。偏微分方程式(微分する変数が2つ以上)については考えません。
想定する微分方程式は以下の形。
$$
y'(t) = f(t, y(t)) \tag{1}
$$
例えば
$$
y' = -a y \tag{2}
$$
とかですね。この解は
$$
y(t) = y(0)e^{-at} \tag{3}
$$
になります。このように(1)を積分して解析解を求めることが可能な場合は、特に数値計算は必要ないです。問題は解析解が求まらない場合。この式と同じ結果が得られるように、与えられた初期値と微分情報から数値積分を使って時刻 t における y の値を求めていくのが「数値的に微分方程式を解く」ということになります。
どういうときに数値計算するのか
有名な話で三体問題というものがあります。「太陽の周りを地球が、地球の周りを月が回っています。ある時刻における3つの天体の位置関係を記述しなさい」というもので、古くから取り組まれてきた問題なのですが、結論から言うとこの問題は(解析的には)解けないことが証明されています。
実用的には、地球は1年で太陽の周りを1週、月も1日で地球の周りを1周します(円近似)、で良いのですが、厳密には引力の相互作用のため完璧な円運動を行っているわけではありません。これら天体の運動は「万有引力に引っ張られて動く3つの質点の運動方程式(微分方程式)」になりますが、この微分方程式が解けないのです。
実際は解けないというよりは、積分しても綺麗な(閉じた)形で解が書けない、が正解ですね。
前項のように式(2)から積分して式(3)が求まるのは超レアケースで、殆どの場合積分できません。その場合は数値計算で頑張って解を求めるしかないのです。
そんな背景があって、「如何に精度良く数値計算を行うか」の研究が発展してきました。
数値解法の種類
まずオイラー法とルンゲクッタ法について簡単に書いておきます。
先にネタバレ的な感じで、図を貼っておきます。
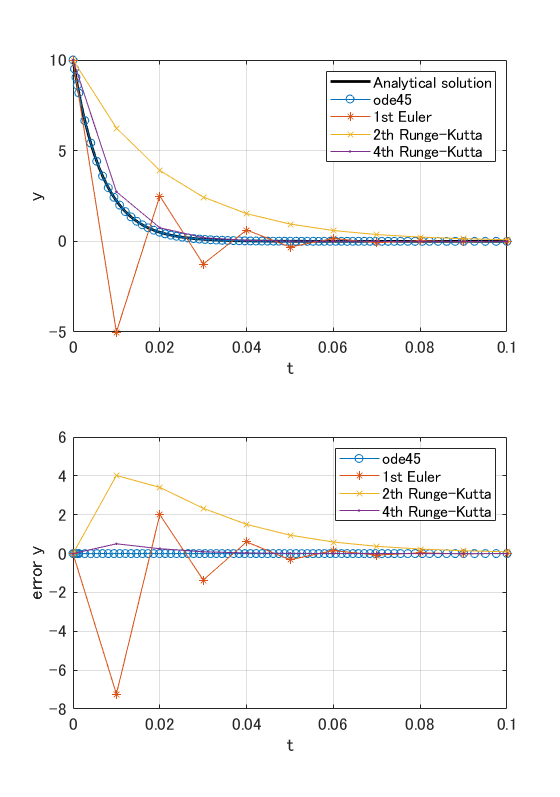
下は(2)式の微分方程式を $a = 150$、初期値 $y_0=10$ として以下のアルゴリズム
- ode45(Dormand-Princean Runge-Kutta):精度保証付き4次Runge-Kutta(ステップ幅可変)
- 1次Euler:1次精度(ステップ幅固定)
- 2次Runge-Kutta:2次精度(ステップ幅固定)
- 4次Runge-Kutta:4次精度(ステップ幅固定)
で計算したものです。
ode45が圧倒的に精度がいいのは、ステップ幅を自動調整してくれてるからなのですが、4次ルンゲクッタも頑張ってますね。
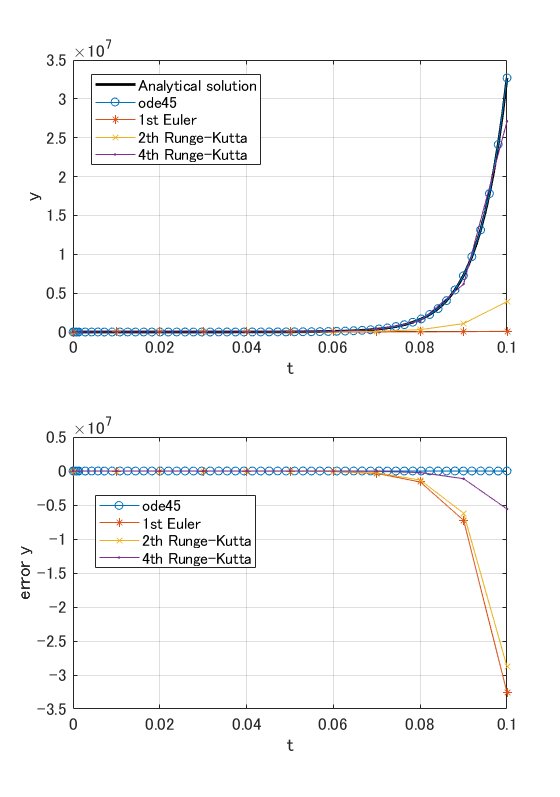
一方で $a = -150$ とした場合はこんな感じ。
値が大きくなるようなケースは、流石に精度保証がないと厳しいですね。
もちろん離散化の幅がode45のほうが小さいので精度が良いのは当たり前なのですが、この幅を調整するにはやはり何か指針がほしいです。そんなときに、要求精度を指定できるode45は強いですね。
1次Euler法
定式化
一番簡単な方法です。数値計算するためには離散化が必要なので、とりあえず (1)式を連続の値から離散式に変換しましょう。今の y の変化量が(1)ですでに与えられているわけですから、微小なステップ幅 h を使って
$$
y_{k+1} = y_k + y'_k h \tag{4}
$$
として逐次計算していけば、今の時刻での y が求まるはずです。これを1次オイラー法と呼びます。
(ホントはステップ幅 dt と書いたほうが分かりやすのですが、通例に習って h にしました。)
計算誤差
さて、このときの計算誤差はどうなるでしょうか。
めちゃくちゃ分かりやすくするために、
$$
y' = t
$$
の微分方程式について計算してみます。今、初期値として t0 で y0 であることが分かっているとしましょう。このときにステップ幅 h だけ先の値 y1 を求めたいとします。
この微分方程式は積分すれば解析解が求まるので(超レアケース!)、真値が容易に計算できます。
$$
y(t) = \frac{1}{2}t^2
$$
これを使えば、y1 の真値は
$$
y_1 = \frac{1}{2}(t_0 + h)^2 = y_0 + t_0h + \frac{1}{2}h^2 \tag{5}
$$
であることがわかります。
一方で、(4)式を使う場合は、t=t0 での傾きが t0 なので、それに h を掛けて
$$
\hat{y_1} = y_0 + t_0h \tag{6}
$$
となります。
(5)、(6)式を比較すると、$ \frac{1}{2}h^2 $ だけ誤差があります。1ステップの計算でステップ幅 dt の2乗に比例した計算誤差(局所誤差と呼ばれる)が乗ってくるので、この数値計算で担保できる精度はせいぜい1次までということになります。このことから、(4)式が1次オイラー法と呼ばれているわけです。
2次Runge-Kutta法
誤差を減らすにはどうすればよいか
オイラー法は1次精度(誤差が2次)でした。この誤差をなんとかして減らしたいですよね。
数値計算によって求めたい関数 y(t) についてテーラー展開をすると
$$
y(t + h) = y(t) + y'(t)h + \frac{1}{2}y''(t)h^2 + \frac{1}{6}y'''(t)h^3+ ... \tag{7}
$$
となるわけですが(ただの公式です)、ルンゲクッタ法の目的は、なるべく簡単な式で、上記の高次項まで考慮することです。上記式を無限に展開していけば精度は出ますが、y(t) の2階微分とか3階微分とか求めたくないですもんね。
連続の式だと見にくいので、離散化しておきましょう。
$$
y_{n+1} = y_n + y_n' h + \frac{1}{2}y_n'' h^2 + \frac{1}{6}y_n''' h^3+ ... \tag{8}
$$
ここから2次のルンゲクッタの導出をしますが、計算がややこしくなるので、(1)式から変数 t を抜き取って、
$$
y'(t) = f(y(t))
$$
に限って話を進めます。
天下り式ですが、以下の式で y の値の更新をする場合を考えます。(a、bは適当な定数です。)
\begin{align}
k_1 &= f(y_n) \tag{9}\\
k_2 &= f(y_n + \frac{dt}{2}k_1) \tag{10} \\
y_{n+1} &= y_n + (a k_1 + b k_2) h \tag{11}\\
\end{align}
新しく k1 と k2 が出てきましたが、別に計算が大変なものではありません。f(y) は既知なので、k1 → k2 の順に計算すれば簡単に求まります。
※「k1 → k2 の順に計算すれば簡単に求まる」ような型がベースなものを陽的ルンゲクッタ、逆にk_1、k_2を求めるのに連立方程式を解く必要がある型を陰的ルンゲクッタと言います。
(この(11)式の a と b をうまく選んであげれば、いい感じに精度が上がらないかなー、と考えながら進みます。)
さて、(11)式に対してテーラー展開を施してやります。連鎖率から
$$
y''(t) = f'(y)f(y) \tag{12}
$$
であることを利用しながら式をいじると
\begin{align}
y_{n+1} &= y_n + \left[ a f(y_n) + b f(y_n + \frac{h}{2}f(y_n)) \right] h\\
& = y_n + \left[ a f(y_n) + b f(y_n) + bf'(y_n)\left(\frac{h}{2}f(y_n)\right) + bf''(y_n)\left(\frac{h}{2}f(y_n)\right)^2 + ... \right]h\\
&= y_n + (a+b)y_n' h + \frac{1}{2}b y_n''h^2 + O(h^3) \tag{13}
\end{align}
となります。連鎖率のおかげで、求めてもない y(t) の二階微分が勝手に出現しました。これがルンゲクッタのすごいところですね。
真値である(8)式と、今求めた(13)式を係数比較してあげれば、
$$
a = 0, \quad b = 1
$$
とすれば、真値の2次項まで計算できることがわかります。これが2次のルンゲクッタ法と呼ばれています。
4次Runge-Kutta法
(8)式のノリで項数をどんどん増やしていけば、精度も上がって行きます。4次のルンゲクッタは以下の式で書かれます。
\begin{align}
k_1 &= f(t_n, y_n), \\
k_2 &= f\left(t_n + \frac{h}{2}, y_n + \frac{h}{2}k_1\right), \\
k_3 &= f\left(t_n + \frac{h}{2}, y_n + \frac{h}{2}k_2 \right), \\
k_4 &= f\left(t_n + \frac{h}{2}, y_n + hk_3 \right), \\
y_{n+1} &= y_n + \frac{h}{6}(k_1+2k_2+2k_3+k_4) \\
\end{align}
この式に沿って計算するだけで、4次オーダーまでの正しさで数値計算できるのです。今更ながらすごいですね。
ちなみに世の中でルンゲクッタというと、大抵の場合4次を指します。5次以上もあるのですが、5次以上は式の形がすごい複雑になるので、世の中の実装はだいたい4次ルンゲクッタがベースになっています。
Embedded Runge-Kutta法(可変ステップ)
ようやく本題の埋め込みルンゲクッタです。こいつはステップ幅をうまいこと自動で制御して、精度の良くルンゲクッタを解こうぜ、なノリの方法の総称です。
最初に説明した通り、基本的な考えは高次と低次(例えば5次と4次)のルンゲクッタの解を比較して、その誤差が大きい場合はステップ幅を小さく、誤差が小さい場合は逆にステップ幅を大きくして、精度向上と計算の効率化を図ります。
ちなみにステップ幅も適当に決めているわけではありません。色々な方法がありますが、例えば下の式である程度最適なステップ幅を決めることができるそうです。
$$
h_{n+1} = 0.9 h_n \left[ \frac{\delta}{\parallel E_{n+1} \parallel_{\infty}} \right]^{1/p+1}
$$
ここで p は低次側のルンゲクッタの次数、En は2種類のルンゲクッタから見積もられる誤差、$\delta$ は最大許容誤差です。
Embedded Runge-Kuttaは、これはこれでたくさん種類があるのですが、初期で有名だったのが多分 Runge-Kutta Fehlbergと呼ばれる手法です。(これの原論文読もうと思ったのですが、NASAのテクニカルレポート(90ページ)だったので諦めました。)
ここからDormandとPrinceanによってさらに改良されたものが、matlabに実装されているode45になります。詳細は次節。
Runge-Kutta Dormand-Princean法
ドーマン・プリンス、って読むんでしょうか。こいつはRunge-Kutta Fehlberg法の欠点を補って、ちょっと精度上げました的な方法です。
[2次のルンゲクッタを導出した部分](# 2次Runge-Kutta法)を読んで気がついた人がいるかもしれませんが、ルンゲクッタは次数を上げていくとパラメータ(2次のルンゲクッタで求めた a と b の値)に自由度が出てきます。
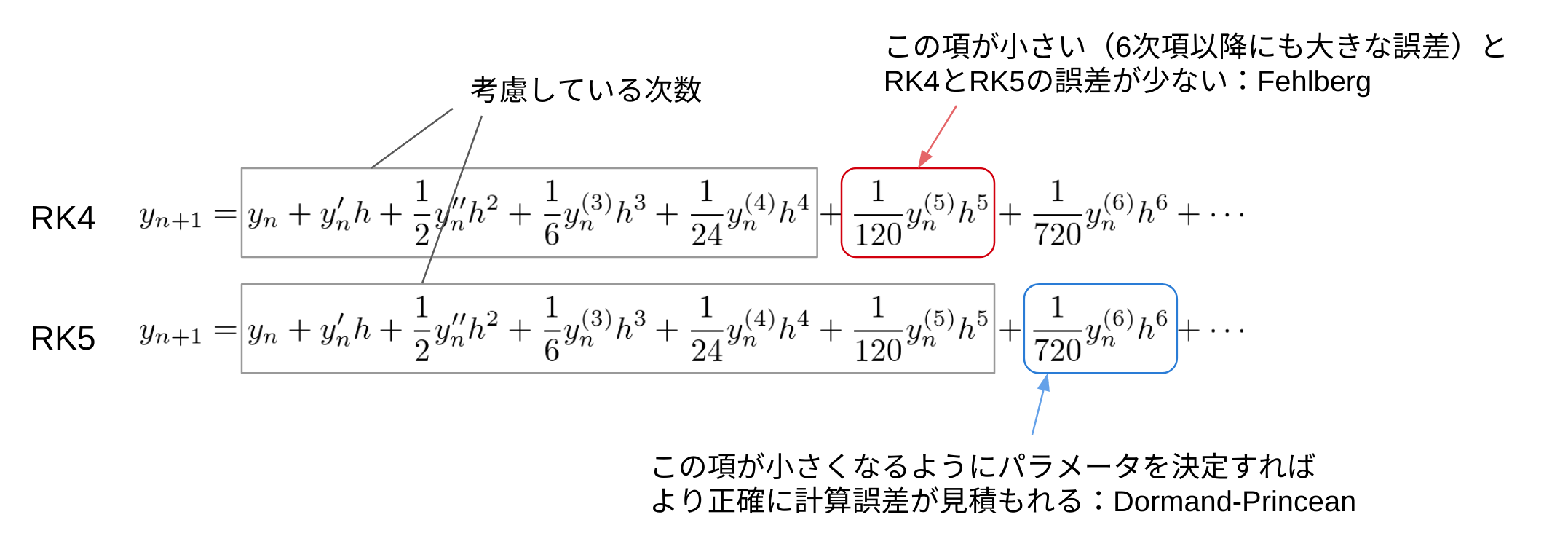
4次のルンゲクッタをそのまま使う場合は、無視される最大次数の5次項が最小になるようにパラメータを求めてあげれば良いのですが、埋め込み型の場合はそれだと困ってしまいます。5次項が小さい値になってしまうと、4次と5次のルンゲクッタの差がほとんどなくなってしまい、適切な誤差評価ができなくなってしまうからです。
そこでDormand-Princean法では、高次側(5次のルンゲクッタ)で無視される最初の項(6次)が最小になるようにパラメータを決めます。
確かに、なんとなく精度が上がるような気がします。
[実際の計算結果](# 数値解放の種類)を見ても分かるとおり、ode45は自動でステップ幅を計算しているので精度が高いです。
参考文献
・Wikipedia(ルンゲ=クッタ法):すごい詳しい
・シキノートさんの記事:すごい分かりやすい
・A family of embedded Runge-Kutta formulae:Dormand-Princeanの論文