はじめに
低音質の音声データを高音質に変換する人工知能(機械学習モデル)が出来ないかと思い、
まずはmnistを使って14×14の画像データを28×28の画像データに復元するプロトタイプを作ってみました。
オートエンコーダについて
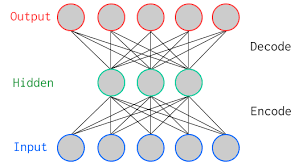
機械学習モデルではオートエンコーダと呼ばれるモデルがあります。一般的なオートエンコーダは、中間層に「入力のデータ量より少ない次元数」のニューロンを用意したモデルです。
中間層は入力層よりも小さいことから、入力した特徴量より少ない特徴量でも数字を識別することが出来ることが分かります。
例えば、mnistのデータ28×28の784次元のデータ数を入力として中間層を64次元、出力層を784次元とした場合、もしこれが正しく人間でも判断できる手書き文字に復元された場合は中間層の64次元では「手書き文字の本質的な構造」を機械学習モデルが発見したことになります。この本質的な構造は人工知能が見つけたものであり、我々人間にも理解できる情報とは限りません。
実際に入力層を784次元として、中間層64次元、出力層784次元でmnistの手書き画像データを学習させてみました。
【以下入力画像】
【100エポック学習後に上記の入力画像を学習後モデルに入力し主る絵よくした結果】
【500エポック学習後に上記の入力画像を学習後モデルに入力し主る絵よくした結果】
このように、64次元のデータ量から728次元の手書き文字画像データにある程度復元することができました。つまり人工知能(オートエンコーダモデル)では728次元のデータを64次元のデータに圧縮して0〜9の手書き文字の本質的な構造を64次元の中で見つけたことが分かります。
情報量を増やす機械学習モデルの理論
とりあえず、全結合して入力層64、中間層を複数設けて出力728にして手書き文字画像を人工知能が人間が認識できるような文字に復元(低画質を高画質に復元)させてみればいいじゃん!!!! って思うかもしれないですが、まぁその通りなんですけど一応理論を考えて実装したので、余談としてお付き合いください。
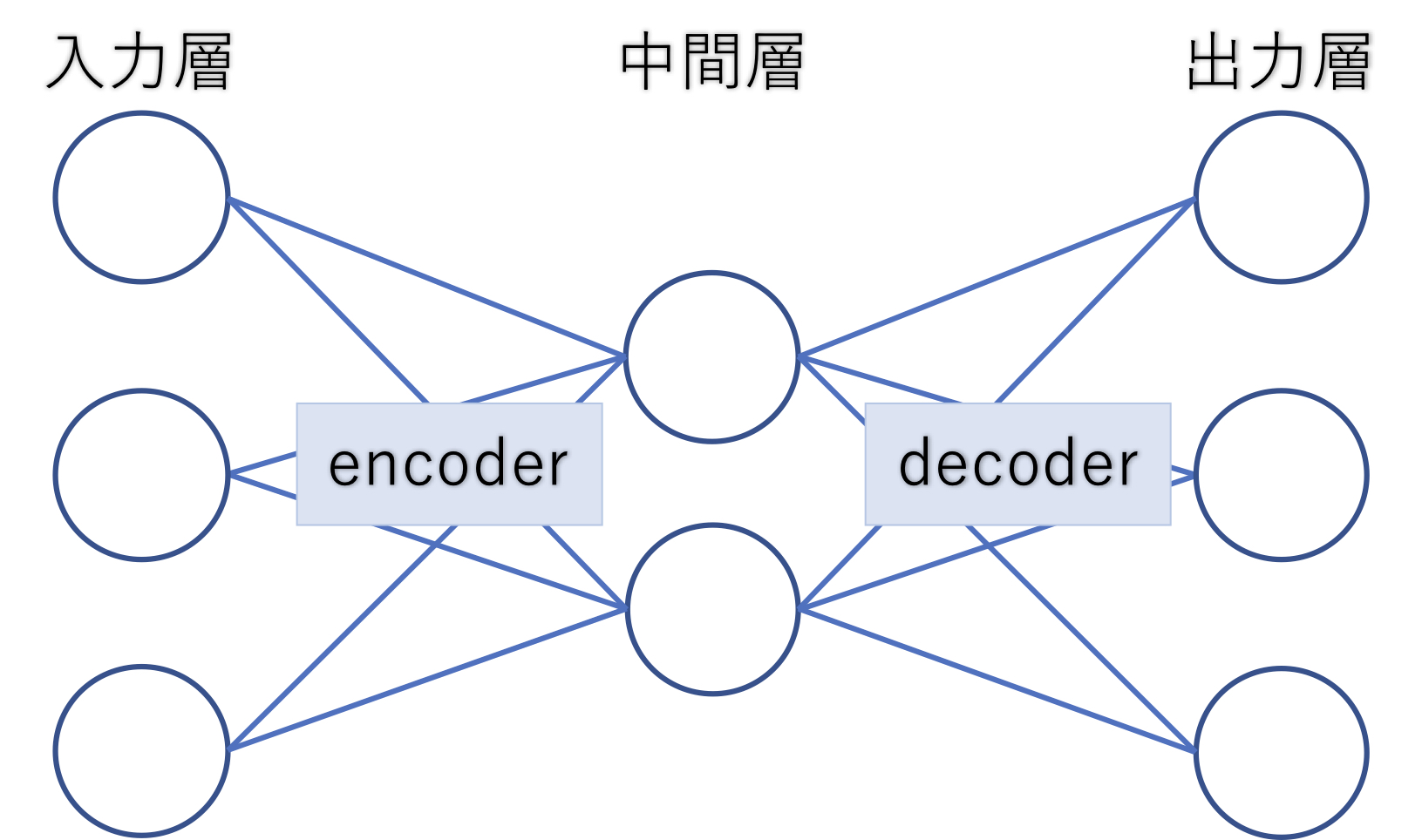
オートエンコーダでは、入力層から入力層より少ない中間層の部分をエンコーダー(encoder)、中間層から中間層より多い次元数の出力層の部分をデコーダー(decoder)と一般的に呼ばれます。
このとき、オートエンコーダモデルで入力層のデータが出力層である程度復元することができた場合、このオートエンコーダモデルでは可逆な関数を求めていることが分かります。
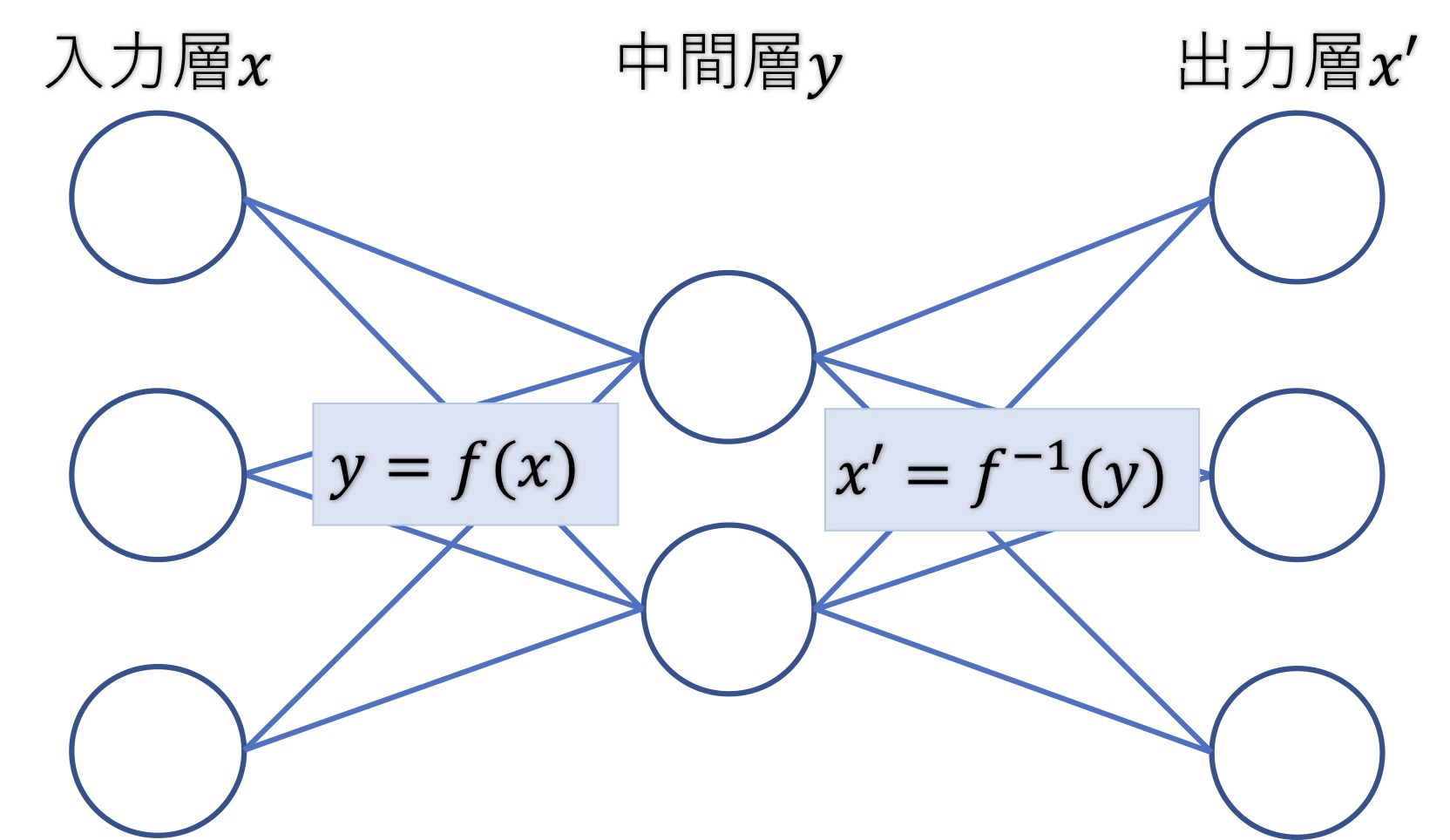
上記で示した画像の通り入力値(入力データ)を$x$、中間層の値を$y$とした場合に、エンコーダ部分では入力$x$を入れると$y$が出力される関数$y=f(x)$がネットワーク層で構築されていることが分かります。
デコーダ部分でも同様に入力値$y$を入れると$x'$が出力される関数$g(y)$がネットワーク層で構築されていることが分かります。このとき、作成したオートエンコーダモデルを通して入力された画像が出力によって元に戻っているのであれば入力値と出力値は$x=x'$であることが分かります。
そうすると、デコーダ部分のネットワーク層で構築された関数$g(x)$はエンコーダ部分のネットワーク層で構築された関数$f(x)$の逆関数$x'=g(y)=f^{-1}(y)$であることが分かります。
んじゃ、人間の手で画像を低画質に圧縮する関数$y=f(x)$を作るから、その圧縮した画像を高画質に復元する$x'=g(y)=f^{-1}(y)$を機械学習モデルに求めてもらおう!!!!
最初っから全結合でやれって話ですね。
情報量を増やす機械学習モデルを実装してみた
早速入力画像サイズ14×14(196次元)、中間層を512、出力される画像サイズを28×28(784次元)にして学習させてみました。
【入力とした画像データ14×14】
14×14の画像サイズだとまだ人間でもなんとなくなんの数字か分かりますね。

【入力とした画像データ14×14を100エポック学習後のモデルに入れて28×28の画像に出力した結果】

4倍の情報量(高画質の画像)に復元することができた!なんとか読める!!!!
よし、調子乗って画像サイズ7×7(196次元)、中間巣を512、出力される画像サイズを28×28(784次元)のモデルを学習させてみました。
【入力とした画像データ7×7】
ちょっと手書き文字の数字が人間でも読めるかどうか怪しくなってきました。
【入力とした画像データ7×7を100エポック学習後のモデルに入れて28×28の画像に出力した結果】
一部は読めないけど、人間がある程度手書き文字を認識できるくらいには復元することができました!
16倍の情報量(高画質画像)にある程度することが出来たし、やっぱ全結合すげぇ
ちなみに、Autoencoderモデルで学習させても可逆な関数(逆関数を持つ$f(x)$)が見つからなかった場合は、入力データを次元圧縮して復元することは出来ません。
まとめ
mnistを利用して情報量を増やす機械学習モデル(ただ全結合しただけ)を作成しました。
これを応用してCD音源をハイレゾ音楽に復元する機械学習モデルを作ってみようかと思います。
流石に音声データだと入力データ量が多いから入力のノードを畳み込んだりして実装しようかなっと思ってます。
あといろんなジャンルの音楽入れると絶対学習発散するから、学習データはピアノ限定にする予定です。
この音声高音質化の取り組みをやってらっしゃる方いたら是非色々教えて下さい〜