はじめに
私は学生の頃は数学科を専門としてなければ、データや統計数理に関わる仕事をしているわけではありません。
数学が好きで独学で統計数理を学んでいるので、間違っている箇所や説明不足のことがあればご指摘をお願い致します。
Stein推定とは
多くの母平均を同時に推定する際に、最小二乗法よりも正確な推定が出来る手法の一つです。いわゆる縮小推定量の一種です。
いま$ N $個の母数$x_1$,$x_2$,$x_3$, , ,$x_N$があり、それぞれの$x_i$について分散$σ$の正規分布$N(x_i,σ)$に従う独立した確率変数$z_1$,$z_2$, , ,$z_N$が観測されたとします。
$x_i$の自然な推定量は$z_i$自身であり、$z_i$は最小分散不偏推定量であり、最尤推定量です。
$z_i$をもとに$x_i$を推定しようとする時、基本的には平均二乗誤差(MSE)を基準とします。この時、$x_i$がどんな値であれ、MSEの和よりも小さい推定量は存在しないとされています。
\sum_{i=1}^{N} E{(\hat{x_i}-x_i)^2}
しかし、$N$が3以上大きい時、MSEの和がより小さくなるような推定量が存在します。それが
James-Stein推定量です。
ただし$N=1,2$の時はzは許容的であり、$N≧3$に対してzは非許容的でありJames-Stein推定量によって改良されます。
\delta = (1-\frac{N-2}{||Z||^2})*z_i
※||Z||^2はユークリッドノルムを示す。
更にJames-Stein推定量より良い推定を出来るようになったのが以下の式から成り立つStein推定量です。
\delta = (1-a)z_i+\frac{N}{a} \sum_{i=1}^{N} y_i
a = \frac{σ^2}{s^2}
s^2 = \frac{1}{N-3} \sum_{i=1}^{N} (y_i - \frac{1}{N}\sum_{i=1}^{n} y_i)^2
検証(James-Stein推定量とMSE)
以下のRプログラムではそれぞれ10個の母数$x_i$,$x_2$, , ,$x_{10}$(1,2,3, , ,10)に対して、それぞれの$x_i$について分散$σ=1$の正規分布$N(x_i,σ)$に従うサンプルを作成します。推定の比較方法としては、各サンプルのMSEとJames-Stein推定量の和を二乗誤差の期待値
E[\sum_{i=1}^{N} (({z_i}-x_i)^2)]
E[\sum_{i=1}^{N} (({\delta_i}-x_i)^2)]
の差で推定を比較したいと思います。
n <- 10
mu <- 1:n
sig <- 1
try_num = 1000
mat <- matrix(0, 1, 2)
## n個のサンプルを発生させる
tmp <- rnorm(n, mu, sig)
xx<-norm(tmp, type="2")^2
## James-Stein推定値を求める
Stein <- (1-(n-2)/(xx)) * tmp
## 結果を保存
mat[1, 1] <- sum((Stein - mu)^2)/n # James-Stein推定値を用いた二乗誤差の期待値
mat[1, 2] <- sum((tmp - mu)^2)/n # データそのものを用いた二乗誤差の期待値
paste("James-Stein : ", mean(mat[, 1]))
paste("MSE : ", mean(mat[, 2]))
何回か試行したところJames-Stein推定値の方がが小さい場合もありますが、MSEの和の値の方が小さい場合もありました。
> paste("James-Stein : ", mean(mat[, 1]))
[1] "James-Stein : 0.566820964708058"
> paste("MSE : ", mean(mat[, 2]))
[1] "MSE : 0.598717547433325"
> paste("James-Stein : ", mean(mat[, 1]))
[1] "James-Stein : 0.697318338422813"
> paste("MSE : ", mean(mat[, 2]))
[1] "MSE : 0.680173749274679"
次に1000回試行してみることにします。
n <- 10
mu <- 1:n
sig <- 1
try_num = 1000
mat <- matrix(0, try_num, 2)
## 1000回実行します
for(i in 1:try_num){
## サンプルを発生させる
tmp <- rnorm(n, mu, sig)
xx<-norm(tmp, type="2")^2
## スタイン推定値を求める
Stein <- (1-(n-2)/(xx)) * tmp
## 結果を保存する
mat[i, 1] <- sum((Stein - mu)^2)/n # スタイン推定値を用いた二乗誤差の期待値
mat[i, 2] <- sum((tmp - mu)^2)/n # データそのものを用いた二乗誤差の期待値
}
paste("Stein : ", mean(mat[, 1]))
paste("MSE : ", mean(mat[, 2])) has
以下のように回数をこなすことにより、James-Stein推定の方が二乗誤差が小さいことがわかりました。
> paste("Stein : ", mean(mat[, 1]))
[1] "Stein : 0.980164575967686"
> paste("MSE : ", mean(mat[, 2]))
[1] "MSE : 0.994713532652209"
検証(Stein推定量とJames-Stein推定量)
では次にJames-Stein推定と改良されたStein推定を比較したいと思います。以下プログラムも先ほどと同じように1000回で検証を行います。
n <- 10
mu <- 1:n
sig <- 1
try_num = 1000
mat <- matrix(0, try_num, 2)
for(i in 1:try_num){
## サンプルを発生させる
tmp <- rnorm(n, mu, sig)
xx<-norm(tmp, type="2")^2
## James-Stein推定値を求める
j_Stein <- (1-(n-2)/(xx)) * tmp
## Stein推定値を求める
s_2 <- (1/(n-3)) * sum((tmp - mean(tmp))^2)
a <- (sig)^2 / s_2
Stein <- (1-a)*tmp + (a/n)*sum(tmp)
## 結果を保存する
mat[i, 1] <- sum((Stein - mu)^2)/n # スタイン推定値を用いた二乗誤差の期待値
mat[i, 2] <- sum((j_Stein - mu)^2)/n # データそのものを用いた二乗誤差の期待値
}
paste("Stein : ", mean(mat[, 1]))
paste("j_Stein : ", mean(mat[, 2]))
結果としてJames-Stein推定値よりStein推定値の方が二乗誤差の期待値が小さいことが分かりました。
> paste("Stein : ", mean(mat[, 1]))
[1] "Stein : 0.943279979128916"
> paste("j_Stein : ", mean(mat[, 2]))
[1] "j_Stein : 0.986703810413371"
検証(Nが増えていく時)
いま$ N $個の母数$x_1$,$x_2$,$x_3$, , ,$x_N$が1,2,3...と増えていった時に、それぞれの推定値がどのように変化するかを可視化したいと思います。
MSE<-c(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)
j_s<-c(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)
s<-c(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)
S1<-0
S2<-0
S3<-0
n <- 30
sig <- 1
try_num = 1000
mat <- matrix(0, try_num, 3)
for(j in 1:n){
mu <- 1:j
for(i in 1:try_num){
## サンプルを発生させる
tmp <- rnorm(j, mu, sig)
xx<-norm(tmp, type="2")^2
## James-stein推定値を求める
if(j>2){
j_stein <- (1-(j-2)/(xx)) * tmp
}else{
j_stein <- (1-(1)/(xx)) * tmp
}
## stein推定値を求める
if(j>3){
s_2 <- (1/(j-3)) * sum((tmp - mean(tmp))^2)
a <- (sig)^2 / s_2
stein <- (1-a)*tmp + (a/j)*sum(tmp)
}else{
s_2 <- sum((tmp - mean(tmp))^2)
a <- (sig)^2 / s_2
stein <- (1-a)*tmp + (a/j)*sum(tmp)
}
## 結果を保存する
S1 <- S1 + sum((tmp - mu)^2)/j # データそのものを用いた二乗誤差の期待値
S2 <- S2 + sum((j_stein - mu)^2)/j # スタイン推定値を用いた二乗誤差の期待値
S3 <- S3 + sum((stein - mu)^2)/j # データそのものを用いた二条誤差の期待値
}
MSE[j] <- S1/100
j_s[j] <- S2/100
s[j] <- S3/100
S1<-0
S2<-0
S3<-0
}
print(MSE)
print(j_s)
print(s)
z<-1:30
plot(z,MSE,xlab="Multivariate normal distribution",ylab="Mean suqured errorloss",pch=3,ylim=c(9,12),type="b",col="royalblue3")
par(new=T)
plot(z,j_s,xlab="Multivariate normal distribution",ylab="Mean suqured errorloss",pch=3,ylim=c(9,12),type="b",col="red")
par(new=T)
plot(z,s,xlab="Multivariate normal distribution",ylab="Mean suqured errorloss",pch=3,ylim=c(9,12),type="b",col="green")
legend("topleft",
legend=c("MSE", "James-stein", "stein"),
pch=c(3,3,3),
lty=c(1,1,1),
col=c("royalblue3", "red", "green")
)
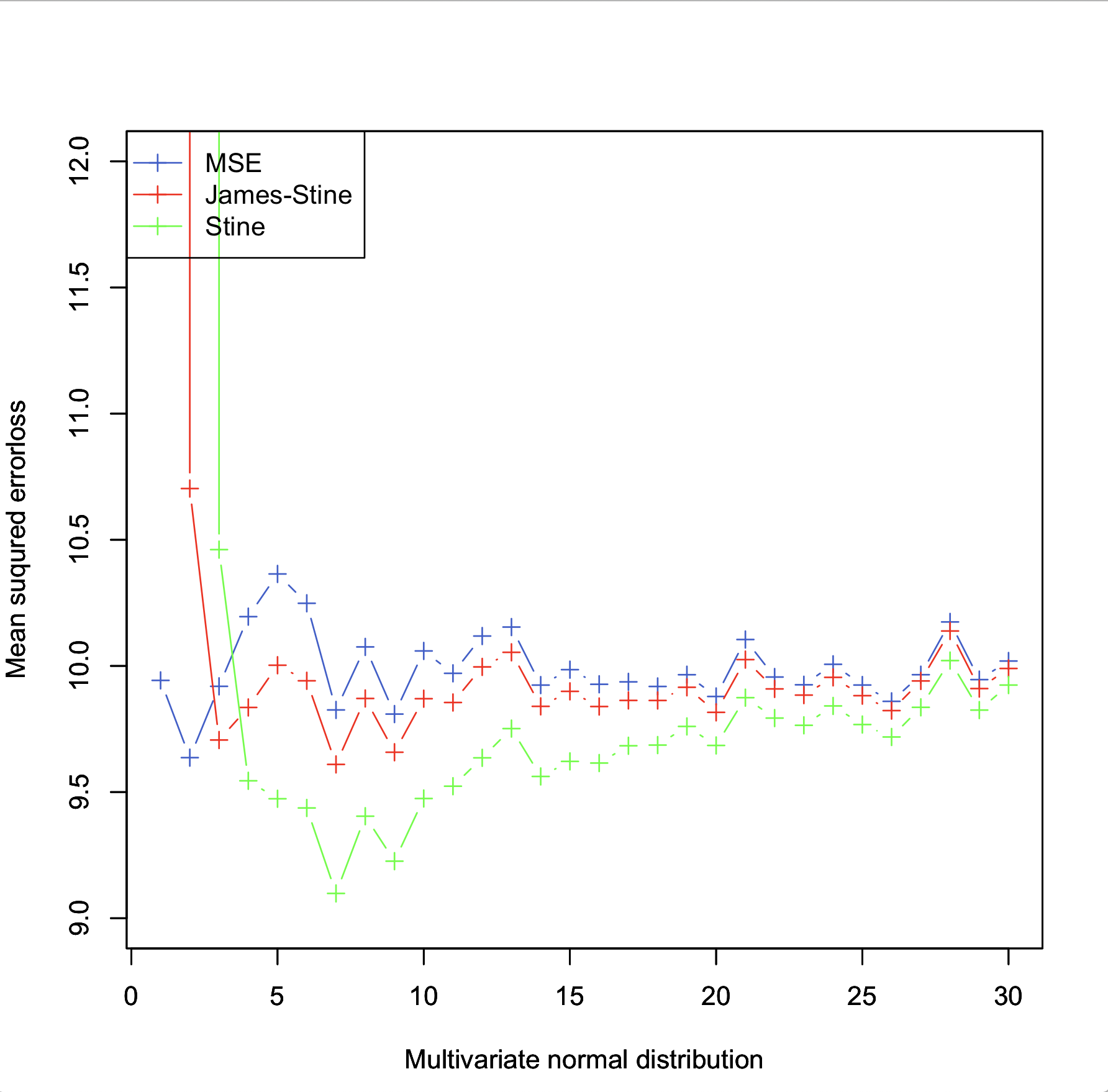
結果からStein推定<James_Stein推定<MSEと二乗誤差が少なく、Stein推定の方が推定がいいことが分かります。
> print(MSE)
[1] 9.893811 10.061190 10.201689 9.991315 10.099179 9.872469 9.984524 10.109032 10.170069 9.929639 10.090521 10.132484 10.112773
[14] 9.938398 9.938122 10.129706 10.003247 9.966152 9.884785 9.984538 9.998484 9.988337 9.895186 9.989390 9.991495 10.203533
[27] 10.052179 9.987638 9.908004 10.070632
> print(j_s)
[1] 1670.078472 11.068689 9.930817 9.705076 9.762386 9.590761 9.726514 9.909983 9.943457 9.762370
[11] 9.961938 10.015718 9.997933 9.850449 9.864478 10.045977 9.931580 9.881776 9.816021 9.915127
[21] 9.959294 9.935525 9.850859 9.950460 9.958395 10.168994 10.009156 9.950454 9.874517 10.045453
> print(s)
[1] NaN 1.399345e+06 1.174287e+01 1.004977e+01 9.381920e+00 9.156616e+00 9.240040e+00 9.404127e+00 9.449622e+00 9.308097e+00
[11] 9.572499e+00 9.637781e+00 9.720924e+00 9.597115e+00 9.675648e+00 9.830977e+00 9.691651e+00 9.719077e+00 9.626047e+00 9.749151e+00
[21] 9.801033e+00 9.801899e+00 9.749940e+00 9.828186e+00 9.872554e+00 1.003455e+01 9.914897e+00 9.867066e+00 9.815286e+00 9.956238e+00
>
まとめ
友人がStein推定について勉強してたのと、機械学習について勉強をしていたら、どこかの論文に"Stein estimator"と書かれていたので、そこからズルズルと推定量について勉強することになりました。
何故Stein推定量が誤差を減少させるのか証明の部分についてはまだ理解していないので、これからも勉強してみようかと思います、