自己符号化器と主成分分析による次元圧縮

はじめに

次元圧縮手法として自己符号化器と主成分分析を実装しました．
教科書として『深層学習』と『はじめてのパターン認識』を使いました．

本記事の構成

• はじめに
• 自己符号化器
• 主成分分析
• 2つの手法の関係
• pythonでの実装
  • auto encoder
  • PCA
• 結果
• おわりに

自己符号化器

自己符号化器（auto encoder） とは，入力を訓練データとして使い，データをよく表す特徴を獲得するニューラルネットワークです．
教師データを使わない教師なし学習に分類され，ニューラルネットワークの事前学習や初期値の決定などの利用されます．
では，自己符号化器の説明に移ります．
以下の図に示すような3層のネットワークを考えます．活性化関数は恒等写像関数 $g(a) = a$ です．

中間層のユニットの値 $z_j$ および出力層のユニットの値 $y_k$ は，入力を順伝播させることで求められます．

\begin{align}
& z_j = \sum_i w_{ji} x_i \\
& \\
& y_k = \sum_j \tilde w_{kj} z_j
\end{align}

中間層のユニットの値を並べたベクトルを $\boldsymbol z$，出力層のユニットの値を並べたベクトルを $\boldsymbol y$，
$w_{ji}$ を $( \ j, i \ )$ 成分に持つ行列を $\boldsymbol W$ とすると以下のように表記できます．

\begin{align}
& \boldsymbol z = \boldsymbol W \boldsymbol x \\
& \\
& \boldsymbol y = \boldsymbol{\tilde W} \boldsymbol z
\end{align}

中間層 $\boldsymbol z$ への変換を 符号化，出力層 $\boldsymbol y$ への変換を 復号化 と呼びます．
自己符号化器では，復号化された $\boldsymbol y$ が，入力 $\boldsymbol x$ に近くなるように学習を行います．
中間層のユニット数が入力次元よりも小さく，入力を再現できれば，次元を圧縮できたことになります．
詳細な学習方法については『pythonでニューラルネットワーク実装』を参照してください．
活性化関数が恒等写像関数なので，微分値は常に $1$ となり，計算がしやすいと思います．

主成分分析

主成分分析（PCA） とは，学習データ $\boldsymbol x_i = (x_{i1}, ..., x_{id})^T$ の分散が最大になる方向への線形変換を求める手法です．
$N$ 個のデータからなるデータ行列を $\boldsymbol X = (\boldsymbol x_1, ..., \boldsymbol x_N)^T$，平均ベクトルを $\boldsymbol{\bar x} = (\bar x_1, ..., \bar x_d)^T$ とします．
データ行列から平均ベクトルを引いたデータ行列 $\boldsymbol{\bar X}$，共分散行列 $\boldsymbol \Sigma$ は以下のようになります．

\begin{align}
& \boldsymbol{\bar X} = (\boldsymbol x_1 - \boldsymbol{\bar x}, ..., \boldsymbol x_N - \boldsymbol{\bar x})^T \\
& \\
& \boldsymbol \Sigma = Var\bigl\{\boldsymbol{\bar X}\bigr\} = \frac{1}{N} \boldsymbol{\bar X}^T \boldsymbol{\bar X}
\end{align}

データ行列 $\boldsymbol{\bar X}$ をある係数ベクトル $\boldsymbol a_j$ で線形変換したものを $\boldsymbol s_j$ すると，変換後のデータの分散は以下のようになります．

\begin{align}
& \boldsymbol s_j = (s_{1j}, ..., s_{Nj})^T \\
& \\
& Var\bigl\{\boldsymbol s_j \bigr\} \varpropto \boldsymbol s_j^T \boldsymbol s_j = \bigl(\boldsymbol{\bar X} \boldsymbol a_j \bigr)^T \boldsymbol{\bar X} \boldsymbol a_j =  \boldsymbol a_j^T \boldsymbol{\bar X}^T \boldsymbol{\bar X} \boldsymbol a_j \varpropto \boldsymbol a_j^T Var\bigl\{\boldsymbol{\bar X}\bigr\} \boldsymbol a_j
\end{align}

この分散を最大にする射影ベクトル $\boldsymbol a_j$ は，ノルムを $1$ に制約したラグランジュ関数を最大化することで求められます．

\begin{align}
& E(\boldsymbol a_j) = \boldsymbol a_j^T Var\bigl\{\boldsymbol{\bar X}\bigr\} \boldsymbol a_j - \lambda (\boldsymbol a_j^T \boldsymbol a_j - 1) \\
& \\
& \frac{\partial E(\boldsymbol a_j)}{\partial \boldsymbol a_j} = 2 Var\bigl\{\boldsymbol{\bar X}\bigr\} \boldsymbol a_j - 2 \lambda \boldsymbol a_j = 0 \\
& \\
& Var\bigl\{\boldsymbol{\bar X}\bigr\} \boldsymbol a_j = \lambda \boldsymbol a_j \tag{*}
\end{align}

式($\ast$)は，元のデータの共分散行列に関する固有値問題を解くことで，分散を最大にする射影ベクトル $\boldsymbol a_j$ が得られることを示しています．
式($\ast$)を解いて得られる固有値を $\lambda_1 \geq ... \geq \lambda_d$ とし，対応する固有ベクトルを $\boldsymbol a_1, ..., \boldsymbol a_d$ とします．
共分散行列は実対称行列であるため，固有ベクトルは互いに直交します．

\boldsymbol a_i^T \boldsymbol a_j = \delta_{ij} = \begin{cases}
1 \ ( \ i = j \ ) \\
\\
0 \ ( \ i \ne j \ )
\end{cases}

最大固有値に対応する固有ベクトルにより線形変換された特徴量を第 $1$ 主成分，
$k$ 番目の固有値に対応する固有ベクトルにより線形変換された特徴量を第 $k$ 主成分と呼びます．
全分散量 $V_{total}$，第 $k$ 主成分の寄与率 $c_k$，第 $k$ 主成分までの累積寄与率 $r_k$ は以下のようになります．

\begin{align}
& V_{total} = \sum_{i = 1}^d \lambda_i \\
& \\
& c_k = \frac{\lambda_k}{V_{total}} \\
& \\
& r_k = \frac{\sum_{i = 1}^k \lambda_i}{V_{total}}
\end{align}

2つの手法の関係

固有値の降順に $\boldsymbol \Sigma$ の $D_y$ 個の固有ベクトルを選び，これを行ベクトルとして格納した行列を $\boldsymbol U_{D_y}$ とします．
入力データの次元数を $D_x$ とすると，$D_y < D_x$ のとき次元が圧縮されます．
$\boldsymbol U_{D_y}$ および $\boldsymbol{\bar x}$ は，以下の最小化問題の解 $(\boldsymbol \Gamma, \boldsymbol \xi) = (\boldsymbol U_{D_y}, \boldsymbol{\bar x})$ となっています．

\min_{\boldsymbol \Gamma, \boldsymbol \xi} \sum_{n = 1}^N \bigl\| \ (\boldsymbol x_n - \boldsymbol \xi) - \boldsymbol \Gamma^T \boldsymbol \Gamma(\boldsymbol x_n - \boldsymbol \xi) \ \bigr\|^2 \tag{**}

主成分分析では，$D_x$ 次元空間内の各データを，二乗距離が最小になるという意味で最もよく表す $D_y$ 次元部分空間を与えていると解釈できます．
中間層および出力層の重みとバイアスを $\boldsymbol W = \boldsymbol \Gamma, \boldsymbol b = -\boldsymbol \Gamma \boldsymbol \xi, \boldsymbol{\tilde W} = \boldsymbol \Gamma^T, \boldsymbol{\tilde b} = \boldsymbol \xi$ とすると，自己符号化器の誤差関数は式($\ast\ast$)と一致します．
つまり，自己符号化器では，$(\boldsymbol \Gamma, \boldsymbol \xi) = (\boldsymbol U_{D_y}, \boldsymbol{\bar x})$ が誤差関数を最小化するネットワークのパラメータとなります．

pythonでの実装

以下のように実装しました．
自己符号化器，主成分分析を分けて掲載します．

auto encoder

圧縮次元を $50$ として処理しています．
学習率 $\varepsilon = 0.00001$ で，$10000$ エポック回しています．

auto_encoder.py

import numpy

class AutoEncoder:

    def __init__(self, n_input, n_hidden):
        self.hidden_weight = numpy.random.randn(n_hidden, n_input + 1)
        self.output_weight = numpy.random.randn(n_input, n_hidden + 1)

    def fit(self, X, epsilon, epoch):
        self.error = numpy.zeros(epoch)
        N = X.shape[0]
        for epo in range(epoch):
            print u'epoch: %d' % epo
            for x in X:
                self.__update_weight(x, epsilon)

            self.error[epo] = self.__calc_error(X)

    def encode(self, X):
        Z = numpy.zeros((X.shape[0], self.hidden_weight.shape[0]))
        Y = numpy.zeros(X.shape)
        for (i, x) in enumerate(X):
            z, y = self.__forward(x)
            Z[i, :] = z
            Y[i, :] = y

        return (Z, Y)

    def __forward(self, x):
        z = self.hidden_weight.dot(numpy.hstack((1, x)))
        y = self.output_weight.dot(numpy.hstack((1, z)))

        return (z, y)

    def __update_weight(self, x, epsilon):
        z, y = self.__forward(x)

        # update output_weight
        output_delta = y - x
        self.output_weight -= epsilon * output_delta.reshape(-1, 1) * numpy.hstack((1, z))

        # update hidden_weight
        hidden_delta = self.output_weight[:, 1:].T.dot(output_delta)
        self.hidden_weight -= epsilon * hidden_delta.reshape(-1, 1) * numpy.hstack((1, x))

    def __calc_error(self, X):
        N = X.shape[0]
        err = 0.0
        for x in X:
            _, y = self.__forward(x)
            err += (y - x).dot(y - x) / 2.0

        return err

main.py

import numpy
import cv2
from sklearn.datasets import fetch_mldata
from auto_encoder import AutoEncoder

if __name__ == '__main__':

    print 'read data...'
    mnist = fetch_mldata('MNIST original', data_home = '.')
    _max = mnist.data[:, :-1].max()
    X = mnist.data[:, :-1] * 1.0 / _max
    input_size = X.shape[1]
    hidden_size = 50
    epsilon = 0.00001
    epoch = 10000
    stride = 50

    print 'auto encoder init...'
    auto = AutoEncoder(input_size, hidden_size)

    print 'train...'
    auto.fit(X[::stride], epsilon, epoch)

    print 'encode...'
    Z, Y = auto.encode(X[::stride])
    for (i, y) in enumerate(Y * _max):
        cv2.imwrite('result/%04d.png' % i, y.reshape(28, 28))

PCA

圧縮次元を $50$ として処理しています．
射影ベクトルおよび復号化した画像を保存しています．

pca.py

import numpy

class PCA:

    def __init__(self, n_components):
        self.n_components = n_components

    def fit(self, X):
        self.bar = self.__bar(X)
        self.cov = self.__cov()
        self.lamda, self.A, self.ccr = self.__solve_eigen_porblem()
        self.S = self.__transformation()

    def decode(self):
        return self.S.dot(self.A.T)

    def __bar(self, X):
        return X - X.mean(axis = 0)

    def __cov(self):
        return numpy.cov(self.bar, rowvar = 0)

    def __solve_eigen_porblem(self):
        _lamda, _A = numpy.linalg.eig(self.cov)
        lamda = _lamda[:self.n_components]
        A = _A[:, :self.n_components]
        ccr = lamda.sum() / _lamda.sum()

        return (lamda, A, ccr)

    def __transformation(self):
        return self.bar.dot(self.A)

main.py

import cv2
from matplotlib import pyplot
from sklearn.datasets import fetch_mldata
import os
from pca import PCA

if __name__ == '__main__':

    print 'read data...'
    mnist = fetch_mldata('MNIST original', data_home = '.')
    X = mnist.data
    n_components = 50
    p_dir = 'projection/'
    d_dir = 'decoded/'

    print 'train...'
    pca = PCA(n_components)
    pca.fit(X)
    print 'cumulative contribution ratio: %f' % pca.ccr

    print 'decode...'
    Xhat = pca.decode()

    print 'save projection vector...'
    if not os.path.exists(p_dir):
        os.mkdir(p_dir)
    for (i, a) in enumerate(pca.A.T):
        fig, ax = pyplot.subplots()
        heatmap = ax.pcolor(a.reshape(28, 28)[:, ::-1], cmap = pyplot.cm.RdYlBu)
        pyplot.savefig(p_dir + '%04d.png' % i, dpi = 25)
        pyplot.clf()

    print 'save decoded images...'
    if not os.path.exists(d_dir):
        os.mkdir(d_dir)
    for (i, xhat) in enumerate(Xhat[::50]):
        cv2.imwrite(d_dir + '%04d.png' % i, xhat.reshape(28, 28))

    n_components = 30
    pca = PCA(n_components)
    pca.fit(X)

    Xhat = pca.A.dot(pca.S.T)
    for (i, xhat) in enumerate(Xhat.T):
        cv2.imwrite('result/%04d.png' % i, xhat.reshape(28, 28))

結果

以下のような結果が得られました．

auto encoder

復号化した画像

誤差

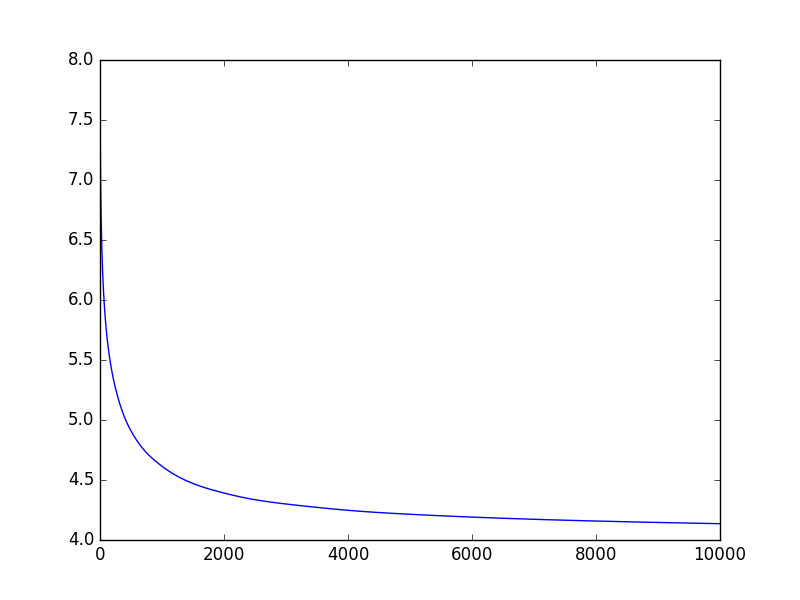
復号化した画像は見栄えのいいものを選びました．
$50$ 次元に圧縮した特徴量から $784$ 次元へ復号化できています．
誤差のグラフは横軸にエポック数，縦軸に誤差の値をとっています．
誤差の桁の差が大きすぎたため，対数をとっています．
厳密な誤差ではありませんが，単調に減少していることがわかります．．

PCA

可視化した射影ベクトル

復号化した画像

射影ベクトルは，固有値の大きい順番に，対応するベクトルを10個選択しました．
左上の射影ベクトルが最も分散の大きい第1主成分へ射影します．
復号化した画像は自己符号化器同様，良い結果が得られています．

おわりに

自己符号化器および主成分分析によって次元を圧縮することができました．