Rabbit Challenge レポート(深層学習 DAY3)

1. 再帰型ニューラルネットワークの概念

RNNとは？

時系列データに対応可能なニューラルネットワークである

例) 音声データ、テキストデータ、(株価など)

$ u^t = W_{(in)}x^t L Wz^{t-1} + b$

$ z^t = f(W_{in}x^t + wz^{t-1} + b)$

$v^t = W_{out}z^t + c$

$y^t = g(W_{out}z^t + c)$

u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W)
z[:,t+1] = functions.sigmoid(u[:,t+1])数式S1)

RNNの特徴

時系列モデルを扱うには、初期の状態と過去の時間t-1の状態を保持し、そこから次の時間でのtを再帰的に求める再帰構造が必要になる

演習

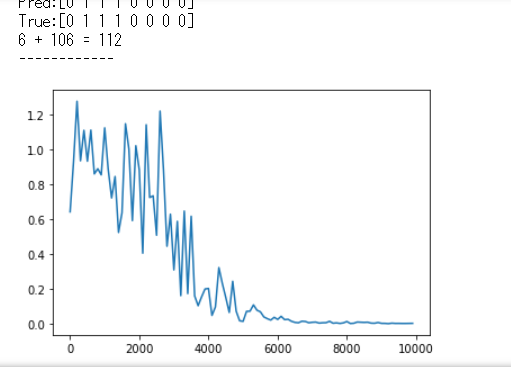
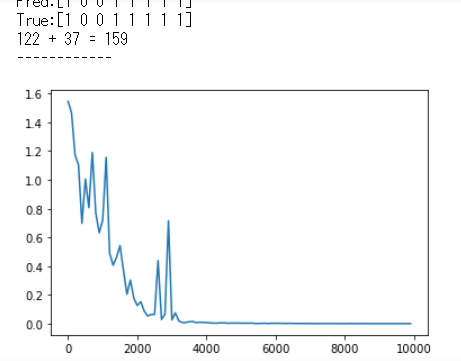
2進数の足し算を予測するプログラムを実行

[try] weight_init_stdやlearning_rate, hidden_layer_sizeを変更してみよう

隠れ層の数を16 -> 32に
hidden_layer_size = 32

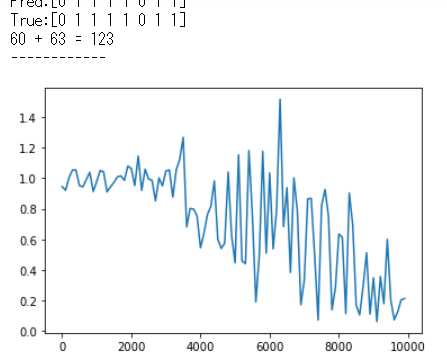
重みを1 -> 5に
weight_init_std = 5

隠れ層を多くすると精度は向上するが、学習の初期は誤差が大きい、
重みを大きくすると学習の初期は誤差が少ないが、そこから勾配爆発してしまう

[try] 重みの初期化方法を変更してみよう

Xavierを適用

W_in = np.random.randn(input_layer_size,hidden_layer_size) / (np.sqrt(input_layer_size))
W_out = np.random.randn(hidden_layer_size,output_layer_size) / (np.sqrt(hidden_layer_size))
W = np.random.randn(hidden_layer_size,hidden_layer_size) / (np.sqrt(hidden_layer_size))

Heを適用

W_in = np.random.randn(input_layer_size,hidden_layer_size) / (np.sqrt(input_layer_size)) * np.sqrt(2)
W_out = np.random.randn(hidden_layer_size,output_layer_size) / (np.sqrt(hidden_layer_size)) * np.sqrt(2)
W = np.random.randn(hidden_layer_size,hidden_layer_size) / (np.sqrt(hidden_layer_size))* np.sqrt(2)

Heのほうが精度がよい

[try] 中間層の活性化関数を変更してみよう

ReLUを適用

# 活性化関数
 z[:,t+1] = functions.relu(u[:,t+1])

# 中間層
delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * functions.d_relu(u[:,t+1])

tanhを適用

#導関数を作成
def d_tanh(x):
    return 1/(np.cosh(x) ** 2)

#活性化関数
z[:,t+1] = np.tanh(u[:,t+1])

# 中間層
delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * d_tanh(u[:,t+1])

どちらも勾配爆発が起こってしまっていることがわかる

BPTT(Backpropagation Through Time)

誤差逆伝播法の考えを利用したもの
長期間の利用には計算量が大きくなり不向きである

$\frac{\partial E}{\partial W_{(in)}} = \frac{\partial E}{\partial u^t} \big[ \frac{\partial u^t}{\partial W_{(in)}} \big]^T = \delta ^t[x^t]^T$

np.dot(X.T, delta[:,t].reshape(1,-1))

$ \frac{\partial E }{\partial W_{in}} = \frac{ \partial E}{ \partial v^t} \big[ \frac{ \partial u^t}{ \partial W_{(out)}}\big] ^t = \delta ^{out,t} [ z^t] ^T$

np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(-1,1))

$\frac{ \partial E }{\partial W} = \frac{\partial E}{\partial u^t} \big[ \frac {\partial u^t}{\partial W} \big] ^t = \delta ^t [z^{t-1}]^T$

np.dot(z[:,t].reshape(-1,1), delta[:,t].reshape(1,-1))

$ \frac{ \partial E}{ \partial u^t} = \frac{\partial E}{ \partial v^t} \frac{\partial v^t}{\partial i^t} = f'(u^t)W_{out}^T \delta^{out,t} = \delta ^t$

delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * functions.d_sigmoid(u[:,t+1])

パラメータの更新

$ W_{(in)}^{t+1} = W_{(in)}^t - \epsilon \frac {\partial E}{ \partial W_{(in)}} = W_{(in)}^t - \epsilon \sum_{z=0}^{T_t} \delta ^{t-z} \big[ x^{t-z} \big] ^T$

W_in -= learning_rate * W_in_grad

$ W_{(out)}^{t+1} = W_{(out)}^t - \epsilon \frac {\partial E}{ \partial W_{(out)}} = W_{(out)}^t - \epsilon \delta ^{out,t} \big[ z^t \big] ^T$

W_out -= learning_rate * W_out_grad

$ W^{t+1} = W^t - \frac{\partial E}{ \partial W} = W_{(in)}^t - \epsilon \sum_{z=0}^{T_t} \delta ^{t-z} \big[ x^{t-z-1} \big] $

W -= learning_rate * W_grad

BPTTの全体像

E^t = loss(y^t,d^t) \\
= loss(g(w_{(out)}z^t + c),d^t) \\
= loss(g(W_{(out)}f(W_{(in)}x^t + Wz^{t-1} + b)+c),d^t)

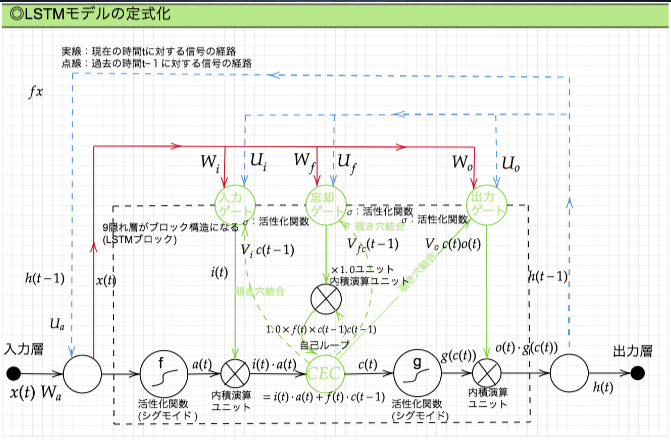
2. LSTM

LSTMとは

時系列を遡れば遡るほど、勾配が消失していく(長い時系列の学習が困難)

⇒ 構造を変えることでその問題を解決したものをLSTMと呼ぶ

勾配爆発

勾配が層を逆伝播するごとに指数関数的に大きくなっていくこと

CEC

勾配消失および勾配爆発の解決方法として、勾配が1であれば解決できる

課題: 入力データについて、時間依存度に関係なく重みが一律である。

⇒ ニューラルネットワークの学習特性が無い

入力ゲートと出力ゲート

それぞれのゲートへの入力値の重みを重み行列W,Uで可変可能とする
=> CECの問題を解決

忘却ゲート

CECは過去の情報がすべて保管されている

課題:　過去の情報が要らなくなった場合、削除することはできず保管され続ける

解決策:　過去の情報が要らなくなった場合、そのタイミングで情報を忘却する機能が必要
⇒忘却ゲートの誕生

覗き穴結合

課題: CECの保存されている過去の情報を、任意のタイミングで他のノードに伝播させたり、あるいは任意のタイミングで忘却させたい。

CEC自身の値に重み行列を介して伝播可能にした構造
⇒　覗き穴結合

3. GRU

GRUとは

従来のLSTMではパラメータが多数存在していた為、計算負荷が大きかった。

しかし、GRUではそのパラメータを大幅に削減し、精度は同等またはそれ以上が望めるようになった構造

4. 双方向RNN

過去の情報だけではなく、未来の情報を加味することで制度を向上させるためのモデル
利用例: 文書の推敲や機械翻訳

5. Seq2Seq

Encoder RNN

ユーザーがインプットしたテキストデータを単語等のトークンに区切って渡す構造

• Talking: 文章を単語等のトークン毎に分割し、トークンごとにIDに分割する
• Embedding: IDからそのトークンを表す分散表現ベクトルに変換
• Encoder RNN: ベクトルを順番にRNNに入力する

• vec1をRNNに入力し、hidden stateを出力。これと次の入力vec2をまたRNNに入力...という風に繰り返す
• 最後のvecを入れた時のhidden stateをfinal stateとしてとっておく。これが入力した分の意味を表すベクトルとなる

Decoder RNN

システムがアウトプットデータを単語等のトークンごとに生成する構造

1.　Decoder RNN: Encoder RNN のfinal state (thought vector) から、各token の生成確率を出力
　　final state をDecoder RNN のinitial state ととして設定し、Embedding を入力
2.　Sampling: 生成確率にもとづいてtoken をランダムに選択
3.　Embedding: 2で選ばれたtoken をEmbedding してDecoder RNN への次の入力とする
4.　Detokenize: 1-3 を繰り返し、2で得られたtoken を文字列に直す。

HRED

Seq2seqの問題

一問一答しかできない。->　HREDを使う

HREDとは

Seq2Seq + Context RNN
過去n-1個の発話から次の発話を生成する
前回の文脈が考慮されるため、より人間らしい文章が生成される

例:
システム:インコかわいいよね。
ユーザー:うん
システム:インコかわいいのわかる。

HREDの課題

• 同じコンテキストを与えられても、答えの内容が毎回会話の流れとしては同じものしか出せない。
• 短く情報量に乏しい答えをしがちである。短いよくある答えを学ぶ傾向がある。
  
  ex)「うん」「そうだね」「・・・」

Context RNN

Encoder のまとめた各文章の系列をまとめて、これまでの会話コンテキスト全体を表すベクトルに変換する構造。

VHRED

VHREDとは？

HREDに、VAEの潜在変数の概念を追加したもの
⇒　HREDの課題を潜在変数の概念を追加することで解決

オートエンコーダー

オートエンコーダーとは

教師なし学習の一つ
そのため学習時の入力データは訓練データのみで教師データは利用しない

• 入力データから潜在変数zに変換するニューラルネットワークをEncoder
• 逆に潜在変数zをインプットとして元画像を復元するニューラルネットワークをDecoder

例: MNISTの場合、28x28の数字の画像を入れて同じ画像を出力するニューラルネットワークということになる

メリット: 次元削減が可能

構造図

VAE

• 通常のオートエンコーダーの場合
  何かしら潜在変数zにデータを押し込めているものの、その構造がどのような状態かわからない。

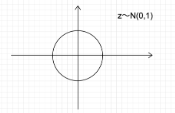
• VAEの場合
  この潜在変数zに確率分布z∼N(0,1)を仮定したもの
  データを潜在変数zの確率分布という構造に押し込めることを可能にする

構造図

6. Word2vec

RNNの課題

単語のような可変長の文字列をNNに与えることはできない

Word2vec

• メリット
  
  大規模データの分散表現の学習が、現実的な計算速度とメモリ量で実現可能にした。
  
  ✗:　ボキャブラリ×ボキャブラリだけの重み行列が誕生。
  
  ○:　ボキャブラリ×任意の単語ベクトル次元で重み行列が誕生。
  

7. Attention Mechanism

seq2seqの課題

• 長い文章への対応が難しい
• seq2seqでは2単語でも100単語でも固定次元ベクトルの中に入力しなければならない

解決策

• 文章が長くなるほどそのシーケンスの内部表現の次元も大きくなっていく仕組みが必要になる
  
  ⇒ 入力と出力のどの単語が関連しているのか」の関連度を学習する仕組みが必要

• 「a」についてはそもそも関連度が低く
• 「I」については「私」との関連度が高い。

確認テスト

復習

Q. サイズ5×5の入力画像を、サイズ3×3のフィルタで畳み込んだ時の出力画像のサイズを答えよ

ストライドは2、パディングは1とする。

A. $OH = OW = \frac{5+2*1-3}{2} + 1 = 3$

確認テスト 1-1

Q.RNNのネットワークには大きくわけて3つの重みがある。1つは入力から現在の中間層を定義する際にかけられる重み、1つは中間層から出力を定義する際にかけられる重み、1つは中間層から出力を定義する際にかけられる重みである。残り１つの重みについて説明せよ。

A.中間層から次の中間層へ受け渡す際の重み

確認テスト 1-2

Q.連鎖律の原理を使い、dz/dxを求めよ

$ z=t^2$

$t=x+y$

A.

$ dz/dt = 2t$

$\frac{dt}{dx} = \frac{dz}{dt} \frac{dt}{dx} = 2t *1 = 2(x+y)$

確認テスト 1-3

Q.下図の$y_1$を$x・s_0：s_1・w_{in}・w・w_{out}$を用いて数式で表せ。

※バイアスは任意の文字で定義せよ

※中間層の出力にシグモイド関数g(x)を作用させよ。

A.
$ z_1 = sigmoid(S_0 w + x_1 w_{(in)} + b)$

$ y1= sigmoid(z_1 W_{(out)} + c)$

確認テスト 2-1

Q.シグモイド関数を微分した時、入力値が0の時に最大値をとる。その値として正しいものを選択肢から選べ

A. (2) （DAY2と同じ問題なので略)

確認テスト 2-2

Q.以下の文章をLSTMに入力し空欄に当てはまる単語を予測したいとする。

文中の「とても」という言葉は空欄の予測においてなくなっても影響を及ば差無いと考えられる。

このような場合、どのゲートが作用すると考えられるか。

A. 忘却ゲート

確認テスト 3-1

Q.LSTMとCECが抱える問題について答えよ

A.

LSTM: 計算負荷が高い

CEC: 入力データにおいて、時間に関係なく重みが等しくなる

確認テスト 3-2

Q. LSTMとGRUの違いについて答えよ

A. GRUのほうがLSTMと比較して計算に必要なパラメータが少なく、精度も高いとされている

確認テスト 5-1

Q.下記の選択肢から、seq2seqについて説明しているものを選べ。
（1）時刻に関して順方向と逆方向のRNNを構成し、それら2つの中間層表現を特徴量として利用するものである。
（2）RNNを用いたEncoder-Decoderモデルの一種であり、機械翻訳などのモデルに使われる。
（3）構文木などの木構造に対して、隣接単語から表現ベクトル（フレーズ）を作るという演算を再帰的に行い（重みは共通）、文全体の表現ベクトルを得るニューラルネットワークである。
（4）RNNの一種であり、単純なRNNにおいて問題となる勾配消失問題をCECとゲートの概念を導入することで解決したものである。

A. (2)

確認テスト 5-2

Q. seq2seqとHRED、HREDとVHREDの違いを簡潔に述べよ。

A.
seq2seqとHRED: 前者は1問1答しかできない。後者はその問題を解決したもの
HREDとVHRED: 前者は文脈に応じた全く同じ回答が返るが、VHREDは毎回変化する

確認テスト 5-3

Q.VAEに関する下記の説明文中の空欄に当てはまる言葉を答えよ。
自己符号化器の潜在変数に____を導入したもの。

A. 確率分布z
[参考]

確認テスト 6-1

Q. RNNとword2vec、seq2seqとAttentionの違いを簡潔に述べよ。
A.
RNNとword2vec: 計算量が異なり、RNNと比較してword2vecは現実的なリソース量で計算できるようになった
seq2se1とAttention: 前者は固定長のものしか学習できなかったものに対し、後者は長い文章の翻訳ができるようになった