Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@taka0518

Rabbit Challenge レポート(機械学習)

Last updated at Posted at 2020-12-24

1. 線形回帰モデル

機械学習モデリングプロセス

  1. 問題設定
  2. データ選定
  3. データの前処理
  4. 機械学習モデルの選定
  5. モデルの選定
  6. モデルの評価

線形回帰

  • 回帰問題

    • 直線で予測 -> 線形回帰
    • 曲線で予測 -> 非線形回帰

  • 回帰で扱うデータ

    • 入力（説明変数or特徴量) $x = (x_1,x_2,・・・,x_m)^{T} \in \mathbb{R}^{m}$
    • 出力（目的変数) $ y \in \mathbb{R}^{m} $

線形回帰モデル

  • 教師あり学習
  • 入力とm次元パラメータの線形結合を出力するモデル(予測値にはハットをつける
\hat{y} = \sum_{j=1}^{m}w_jx_j+w_0
  • モデルのパラメーター
    • 特徴量が予測値に対してどのように影響を与えるかを決定する重みの集合
    • 最小二乗法により推定

ハンズオン

ボストンの住宅データセットを線形回帰モデルで分析

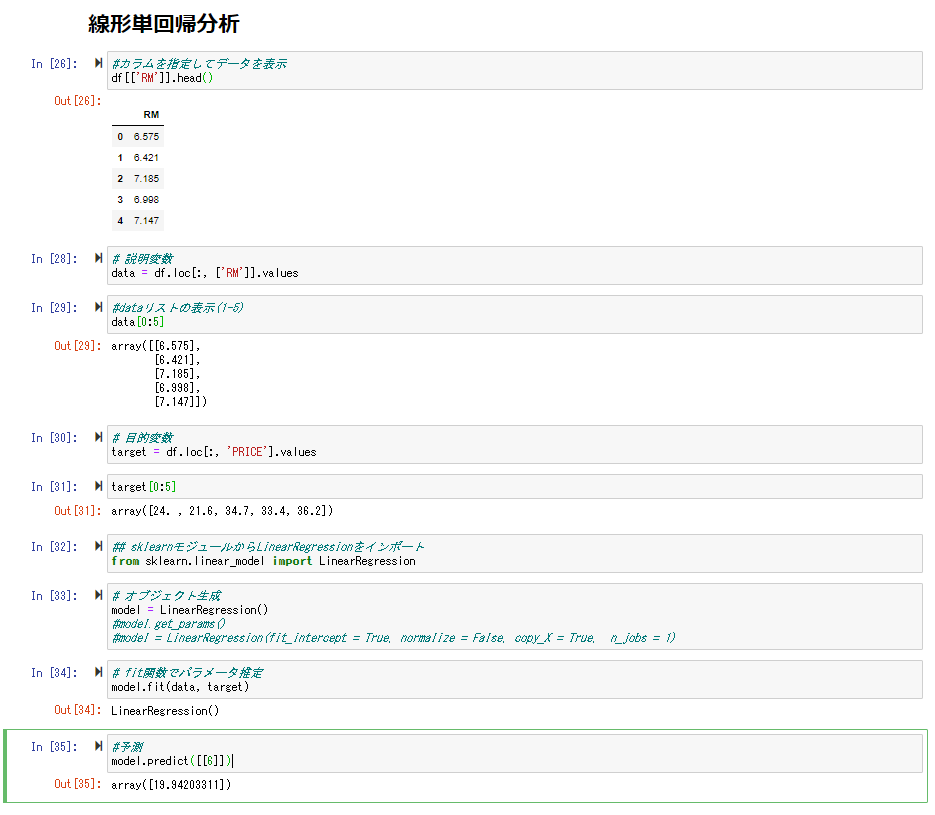
線形単回帰分析

説明変数を部屋数、目的変数を価格としてモデルを作成。

作成したモデルに部屋数「6」での価格を予測させた所、「19.94203311」という値が予測できた。

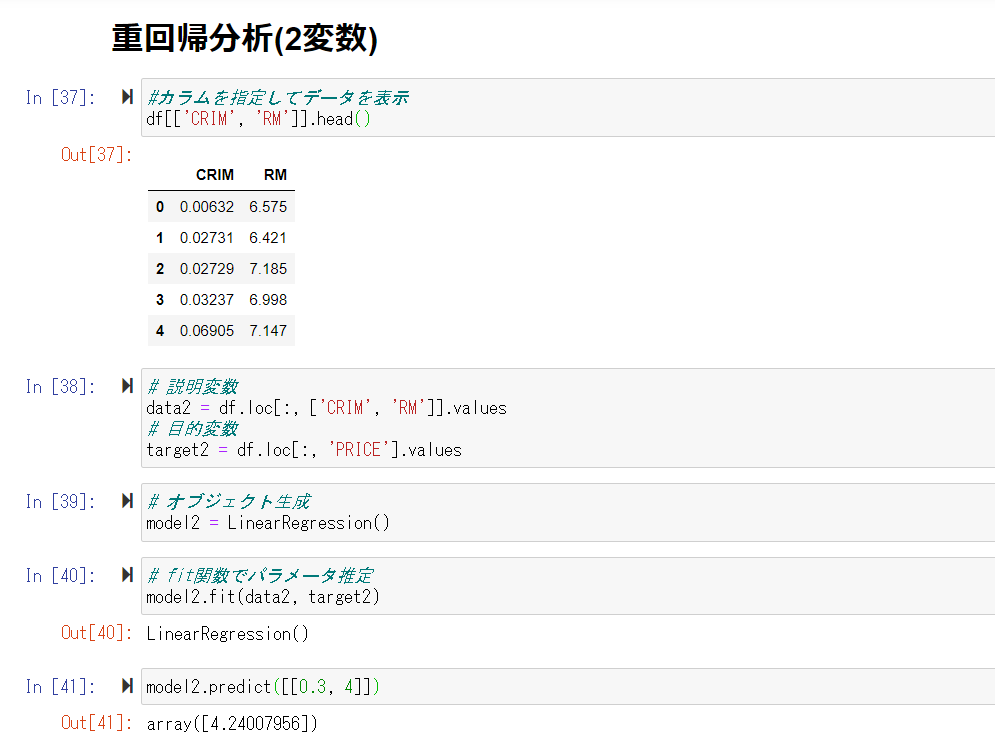
image.png

重回帰分析

次に犯罪率、部屋数から価格を予測する。

[課題] 部屋数が4で犯罪数が0.3の物件の価格を予測。「4.24007956」という値が予測できた。

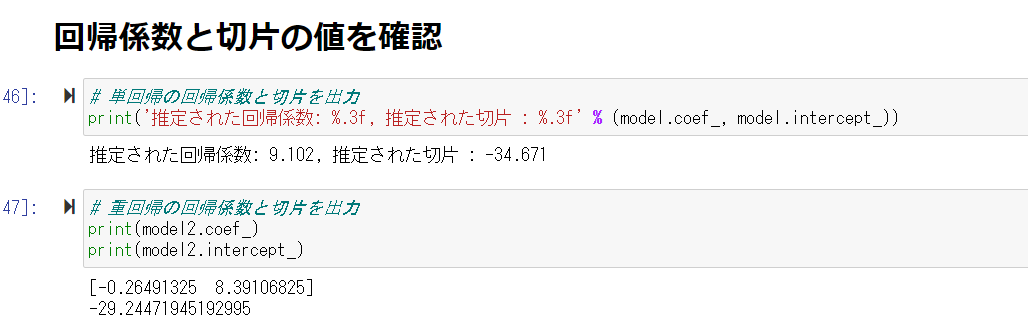
image.png

回帰係数と切片の値を確認

犯罪率が上がるほど価格は下がり、部屋の数が増えるほど価格が上がることがわかる。

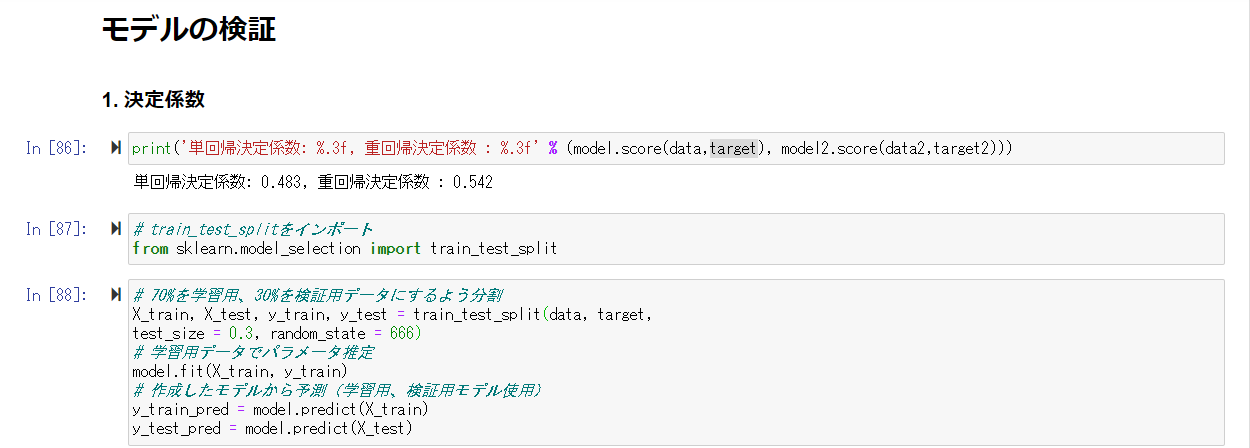
image.png

モデルの検証

  • 決定係数
    • 説明変数が目的変数のどれぐらいを説明できるかを表す値
    • 残差の二乗和を標本地の平均値yからの偏差の二乗和で割ったものを1から引いた値
    • 最小二乗法はこの定義を最大にするようなパラメータの選択方法である

先ほど利用したデータを学習用、検証用に分割しモデルを作成。

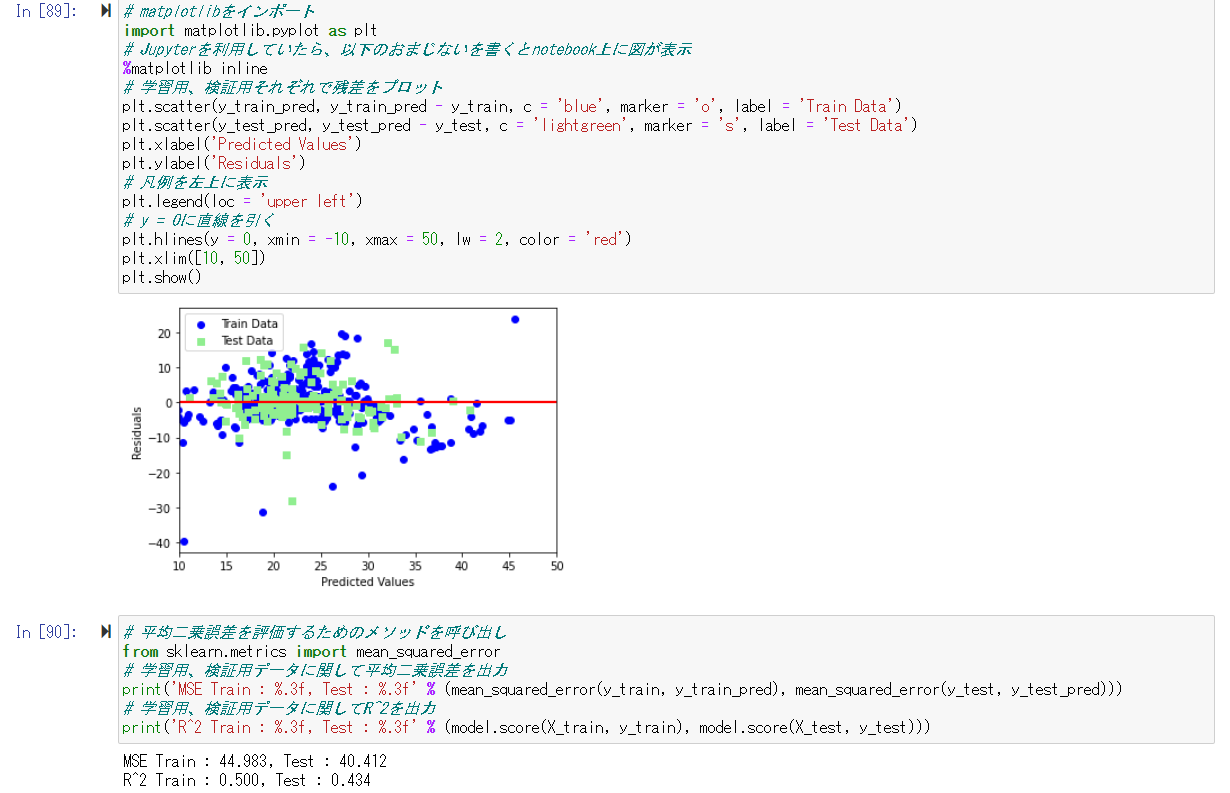
作成したモデルから学習用データ、検証用データに対しての予測を行う

image.png

image.png

決定係数は「0.434」となっており、よい精度とはならなかったことがわかる。

#2. 非線形回帰モデル

基底展開法

  • 回帰関数として、基底関数と呼ばれる既知の非線形関数とパラメータベクトルの線形結合を使用
  • 未知パラメータは線形回帰モデルと同様に最小2乗法や最尤法により推定
  • 基底関数として、多項式関数、ガウス型基底関数、スプライン関数などがよく利用される
y_{i} = f(x_i) + ε_i = w_o + \sum_{i=1}^{m} w_i\phi_j(x_i) + \epsilon_i
  • 説明変数
    • $x_i = (x_{i1},x_{i2},・・・,x_{im} ) \in \mathbb{R}^{m}$
  • 非線形関数ベクトル
    • $\phi(x_i) = (\phi_1(x_i),\phi_2(x_i),・・・\phi_k(x_i))^{T} \in \mathbb{R}^{k}$
  • 非線形関数の計画行列
    • $ \phi^{(train)} = (\phi_1(x_i),\phi_2(x_i),・・・\phi_k(x_i))^{T} \in \mathbb{R}^{n×k}$
  • 最尤法による予測値
    • $\hat{y} = \phi(\phi^{(train)T}\phi^{(train)})^{-1} \phi^{(train)T}y^{(train)}$

未学習(underfitting)

学習データに対して、十分小さな誤差が得られないモデル

  • 対策
    • 表現力の高いモデルを利用する

過学習(overfitting)

小さな誤差は得られたが、テスト集合誤差との差が大きいモデル

  • 対策
    • 学習データの数を増やす
    • 不要な基底関数を削除して表現力を抑止
      • 解きたい問題に対して多くの基底関数を用意してしまうと、過学習が発生する
    • 正則化法を利用して表現力を抑止

正則化法

モデルの複雑さに伴って、その値が大きくなる正則化項を課した関数を最小化する方法

単純にMSEを最小にする点を求めるのではなく、パラメータに制約を与え(原点に近づける)、その中でMSEを最小にする点を求める

S_\gamma = (y-\phi w)^{T}(y-\phi w) + \gamma R(w) \quad \gamma(>0)

正則化項

いくつもの種類があり、それぞれで推定量の性質が異なる

  • なし: ただの最小二乗推定量
  • L2ノルムを利用：Ridge推定量
    • ⇒ 縮小推定: パラメータを0に近づけるように推定
  • L1ノルムを利用：Lasso推定量
    • ⇒ スパース推定：いくつかのパラメーターを0に推定できる

正則化パラメータ

モデルの曲線のなめらかさを調節　

汎化性能

  • 学習に使用した入力だけではなく、未知のデータに対する予測性能
  • 汎化誤差が小さいものが良い性能を持ったモデルといえる

ホールドアウト法

有限のデータを学習用とテスト用の2つに分割し、予測精度や誤り率を推定する

  • 学習用を多くすればテスト用が減り学習制度はよくなるが、性能評価の精度は悪くなる
  • 手元に大量にデータがある場合を除いて、良い性能評価を与えないという欠点がある

基底展開法に基づく非線形回帰モデルでは、基底関数の数、位置、バンド幅の値とチューニングパラメータをホールドアウト値を小さくするモデルで決定する

交差検証法(クロスバリデーション)

検証データが被らないように複数のパターンでデータを分割し、モデルを作成する

それぞれで作ったモデルの精度の平均をCV値とし、

その中から一番良いモデルを採用する

3.ロジスティック回帰モデル

  • 分類問題(クラス分類)
  • 分類で扱うデータ
    • 入力(説明変数、特徴量)
      • m次元のベクトル
    • 出力(目的変数)
      • 0 or 1

説明変数: $ x = (x_1,x_2,・・・,x_m)^{T} \in \mathbb{R}^{m}$

目的変数: $y = \in {0,1}$

教師データ: ${(xi,yi);i = 1,・・・,n}$

ロジスティック線形回帰モデル

分類問題を解くための教師あり機械学習モデル

  • 入力とm次元パラメータの線形結合をシグモイド関数に入力
  • 出力はy=1になる確率の値になる

パラメータ: $ w = (w_1,w_2,・・・,w_m)^T \in \mathbb{R}^m$

線形結合: $ \hat{y} = w^Tx + w_0 = \sum_{j=1}^m w_jx_j + w_0$

シグモイド関数

  • 入力は実数・出力は必ず0~1の間
  • (クラス１に分類される)確率を表現
  • 単調増加関数
  • パラメータ(a）を変化されることで関数の形が変化する
\sigma(x) = \frac{1}{1+exp(-ax)}

シグモイド関数の性質

  • シグモイド関数の微分は、シグモイド関数自身で表現することが可能
  • 尤度関数の微分を行う際にこの事実を利用すると計算が用意
\frac{∂\sigma(x)}{∂x} = \frac{∂}{∂x}\bigg(\frac{1}{1+exp(-ax)}\bigg) \\
= (-1)\{1+exp(-ax)\}^{-2}exp(-ax)(-a) \\
= a\sigma(x) (1-\sigma(x))

ベルヌーイ分布

確率$p$で1,確率$1-p$で0をとる、離散確率分布（例：コイン投げ)

ある分布を考えた時、そのパラメータ(既知)によって、生成されるデータは変化する

データからそのデータを生成したであろう尤もらしい分布を推定したい(最尤推定)

  • 同時確率
    • あるデータが得られたとき、それが同時に得られる確率
    • 確率変数は独立であることを仮定すると、それぞれの確率の掛け算となる
  • 尤度関数
    • データは固定し、パラメータを変化させる
    • 尤度関数を最大化するようなパラメータを選ぶ推定を最尤推定という
P(y_1,y_2,・・・,y_n;p) = ∏_{i=1}^np^{yi}(1-p)^{1-y_i}

ロジスティック回帰モデルの最尤推定

尤度関数とは結局のところ、$w$のみに依存する関数となる

P(y_1,y_2,・・・,y_n|w_0,w_1,・・・,w_m) = ∏_{i=1}^{n}p_i^{yi}(1-p_i)^{1-y_i} \\
= ∏_{i=1}^{n}\sigma(w^Tx_i)^{yi}(1-\sigma(w^Tx_i))^{1-y_i} \\
= L(w)

勾配降下法(Gradient descent)

反復学習によりパラメータを逐次的に更新するアプローチの一つ

$\eta$は学習率と呼ばれるハイパーパラメーターでモデルのパラメータの収束しやすさを調整

パラメータが更新されなくなった場合、勾配が0=反復学習で探索した範囲では最適な解が求められたということとなる

w(k+1) = w^k - \eta\frac{∂E(w)}{∂w}

確率的勾配法(SGD)

データを一つずつランダムに選んでパラメータを更新

勾配降下法でパラメータを1回更新するのと同じ計算量でパラメータをn回更新できるので効率よく最適な解を探索可能

w(k+1) = w^k + \eta(y_i - p_i)x_i

モデルの評価

正解率

正解した数/予測対象となった全データ数

分類したいクラスには偏りがあることが多く、単純な正解率ではあまり意味が無い事が多い

\frac{TP + TN}{TP + FN + FP +TN}

再現率(Recall)

本当にPositiveなものの中からPositiveと予測できる割合

謝りが多少多くても抜け漏れが少ない予測をしたい際に利用

\frac{TP}{TP+FN}

適合率(Precision)

モデルがPositiveと予測したものの中で本当にPositiveである割合

見逃しが多くてもより正確な予測をしたい際に利用

\frac{TP}{TP+FP}

F値

RecallとPrecisionの調和平均

高ければ高いほどどちらの値も高くなる

ハンズオン

タイタニックの乗客データを利用して、ロジスティック回帰モデルを作成

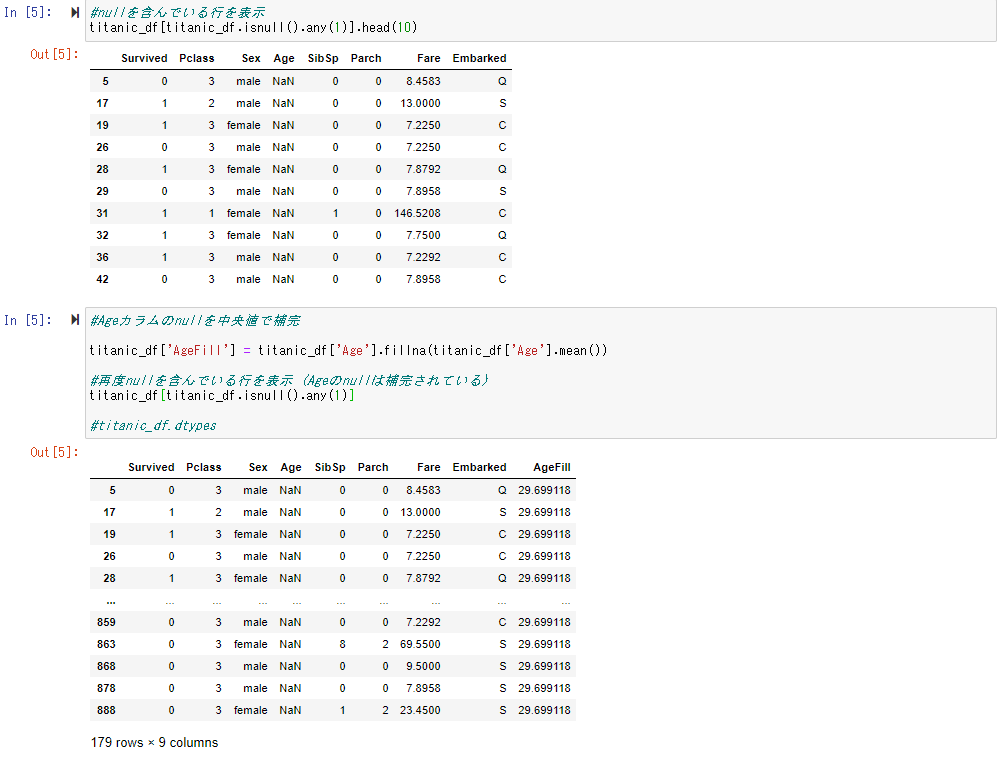
欠損している年齢データを平均値を用いて補完する

image.png

1変数から生死を判別する

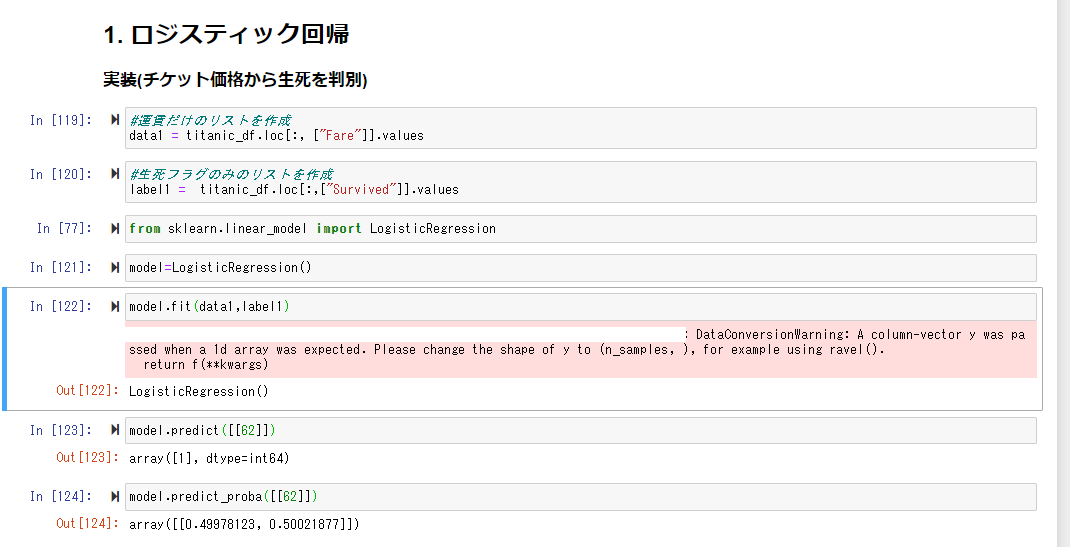
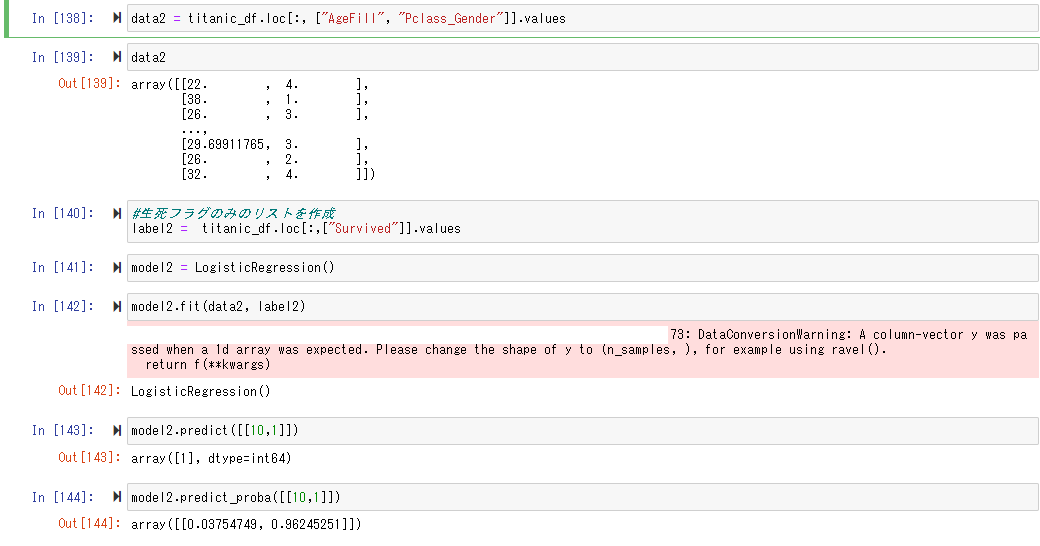
まず条件を運賃のみに絞った場合の生死を判別する

作成したモデルを利用し、運賃「62」の乗客は生き残る、ということが分かった

model_predict_probaというAPIを使うことで、確率pの値が分かる

image.png

2変数から生死を判別する

性別や階級を考慮する為に、femaleを0,maleを1とし、更にその値をPclass(階級、低いほどよい)と値を足し合わせることでPclass_Genderという値を設定。

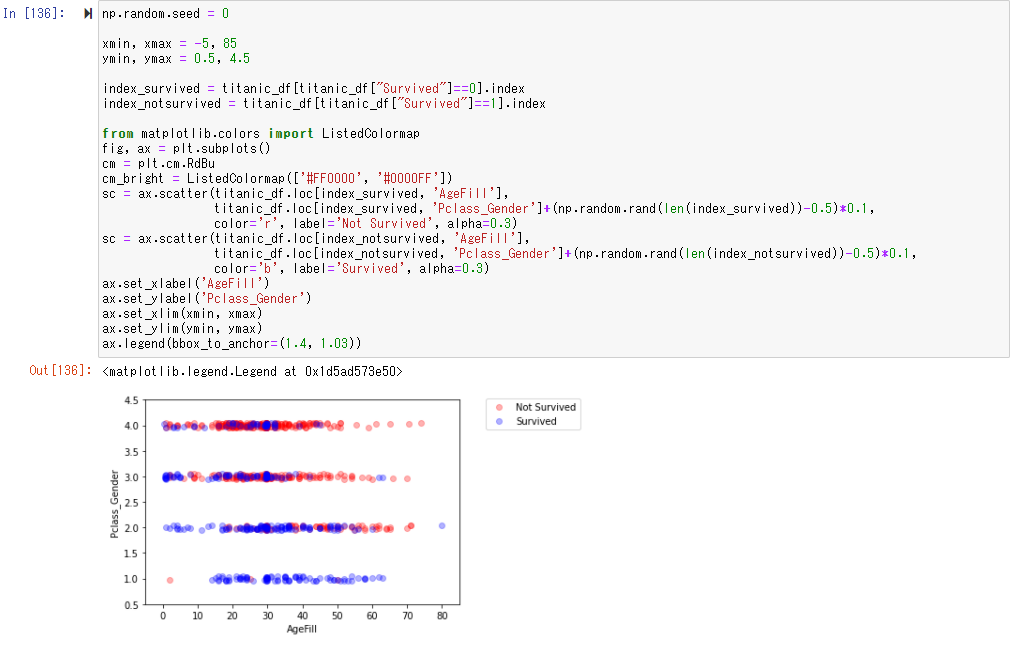
Pclass_Genderと年齢を軸に生死の関係性をグラフに表す

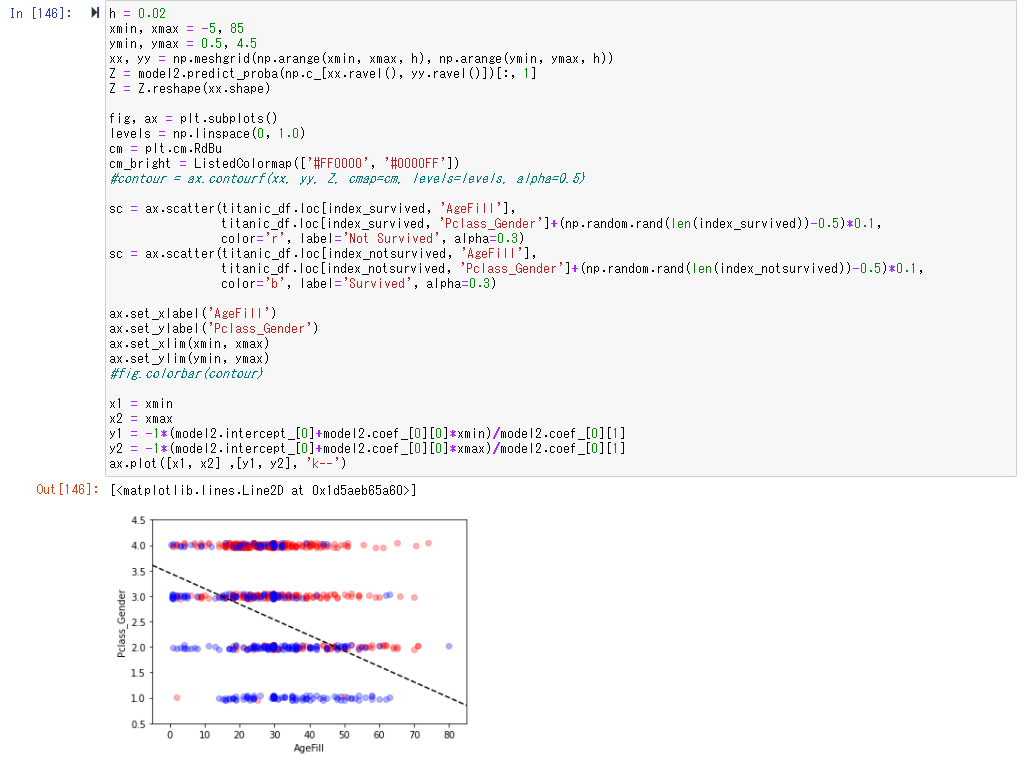
image.png

Pclass_Genderと年齢を説明変数とし、生死を判定するロジスティック回帰モデルを作成

「10歳」でPclass_Genderが「1」は生き残り、その確率もかなり高い値となっていることがわかる

image.png

プロットしてみると、年齢が低く、Pclass_Genderが少ないほど生存する可能性は高くなっていることがわかる

image.png

課題

年齢が30歳で男の乗客は生き残れるか？

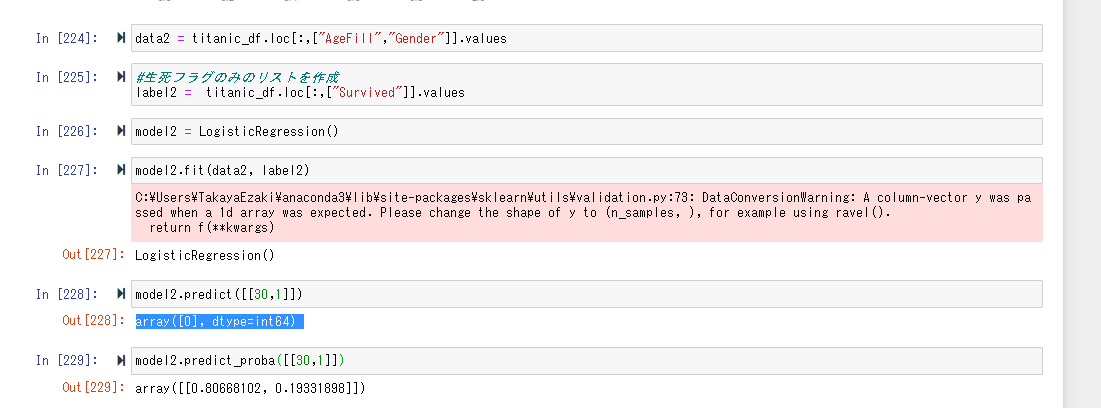
「AgeFill」と「Gender」を説明変数にとりモデルを生成。

結果は「0」で死亡。また生存する可能性は「0.1933..」とかなり低い値となった。

image.png

4.主成分分析

多変量データの持つ構造をより少数個の指標に圧縮(例:3次元データを2次元にする)

  • 変量の個数を減らすことに伴う、情報の損失を小さくしたい
  • 少数変数を利用した分析や可視化が実現可能

学習データ $ x_i = (x_{i1},x_{i2},・・・,x_{im}) \in \mathbb{R}^{m}$

平均(ベクトル) $ \vec{x} = \frac{1}{n}\sum_{i=1}^n x_i$

データ行列 $ \vec{X} = (x_1 - \vec{x},・・・,x_n - \vec{x} )^T$

分散共分散行列 $ \sum = Var(\vec{X}) = \frac{1}{n}\vec{X}^T\vec{X}$

線形変換後のベクトル $s_j = (s_{1j}、・・,s_{nj})^T = \vec{X}a_j \ a_j \in \mathbb{R}^m$

線形変換後の分散 $Var(s_j) = \frac{1}{n}s_{j}^Ts_j = \frac{1}{n}(\vec{x}a_j)^T(\vec{x}a_j) = \frac{1}{n}a_j^T\vec{X}^T\vec{X}a_j = a_j^TVar(\vec{X})a_j$

ラグランジュ関数

以下のような制約付き最適化問題を解く(ノルムが1となるようにする)

目的関数 $arg \quad \max_{a \in \mathbb{R}^m} a_j^T Var(\vec{X})a_j$

制約条件 $ a_j^Ta_j = 1$

この場合、ラグランジュ関数を最大にする係数ベクトルを探索すればよい

 E(a_j) = a_j^T Var(\vec{X})a_j-\lambda(a_j^Ta_j-1)$

微分すると元データの分散共分散行列の固有値と固有ベクトルが解となる。

\frac{\theta E(a_k)}{\theta a_j} = 2Var(\vec{X})a_j - 2\lambda a_j = 0 \\

⇒ $Var(\vec{X})a_j = \lambda a_j

射影先の分散=固有値となる

Var(s_1) = a_1^TVar(\vec{X})a_1 = \lambda_1a_1^Ta_1 = \lambda_1

寄与率

第k主成分の分散の全分散に対する割合(第k主成分の分散/主成分の総分散)

    c_k = \frac{\lambda _k}{ \sum_{i=1}^m \lambda_i}

累積寄与率

第1-k主成分まで圧縮した際の情報損失量の割合(第1~k主成分の分散/主成分の総分散)

    r_k = \frac{\sum_{j=1}^k \lambda _j}{\sum_{i=1}^m \lambda _i}

ハンズオン

ロジスティック回帰

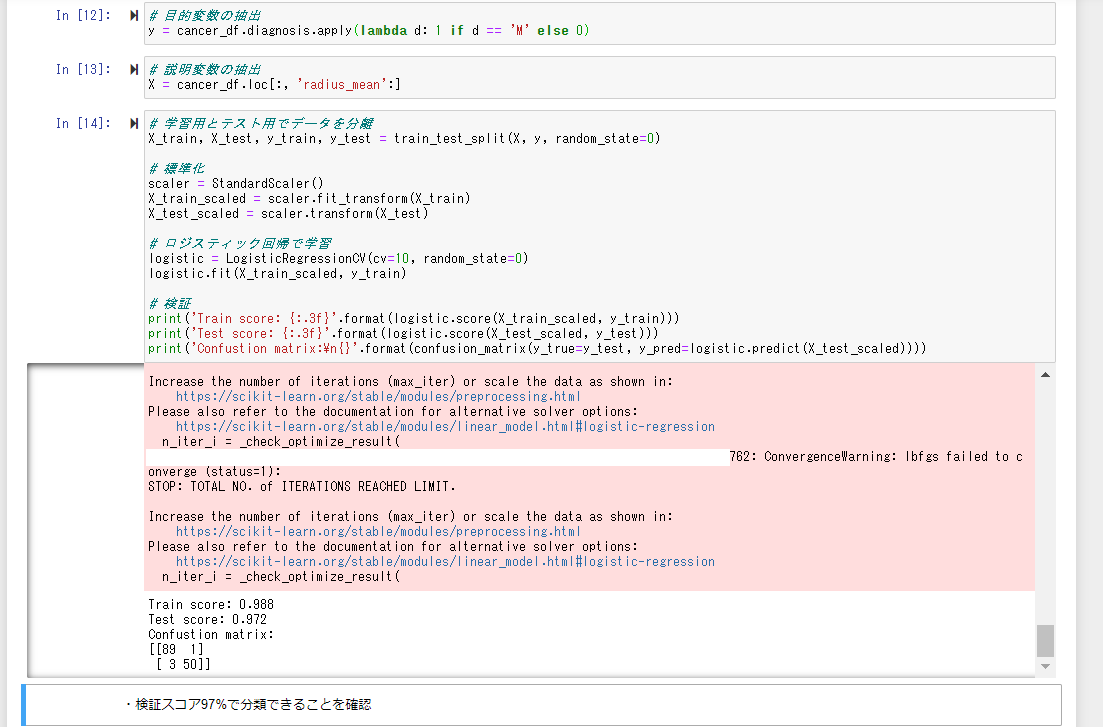
30次元のデータを使ってロジスティック回帰をしてみる

この時点でも97%が分類できていることが確認できる

image.png

主成分分析

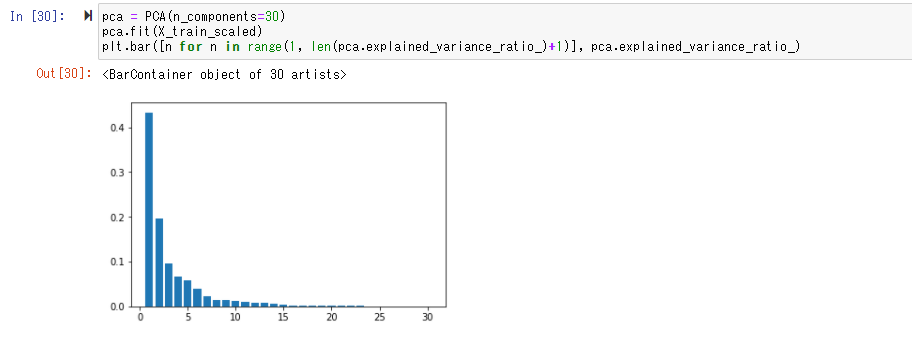
まずは30次元のデータを30個の主成分で次元圧縮をし、それぞれの主成分の情報量を求める

第一主成分は約40%,第二主成分は20％..の情報量があると読み取れる

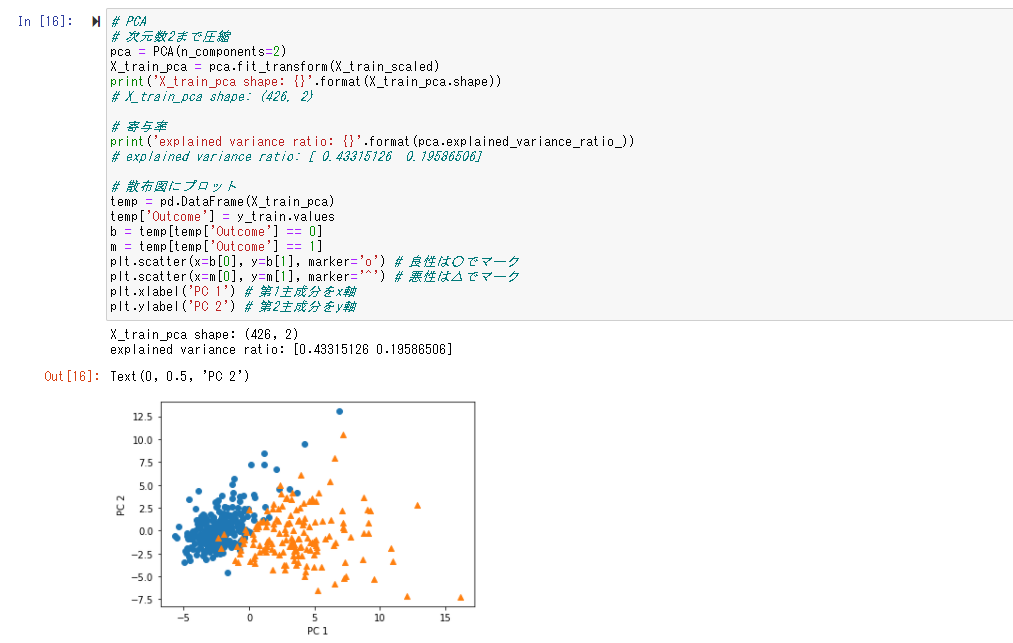
image.png

次にこれらを2次元まで圧縮した結果を以下のようにプロットする。

97%分類できていたデータでも、2次元まで圧縮すると60%ほどの情報量しか持たず、うまく境界を引くことはできないが、可視化することはイメージがしやすくなる等のメリットがあるので使い分けていく必要がある。

image.png

5.アルゴリズム

k近傍法(KNN)

分類問題の為の機械学習手法

最近傍のデータｋ個を取ってきて、それらがもっとも多く所属するクラスに識別

ハンズオン

課題

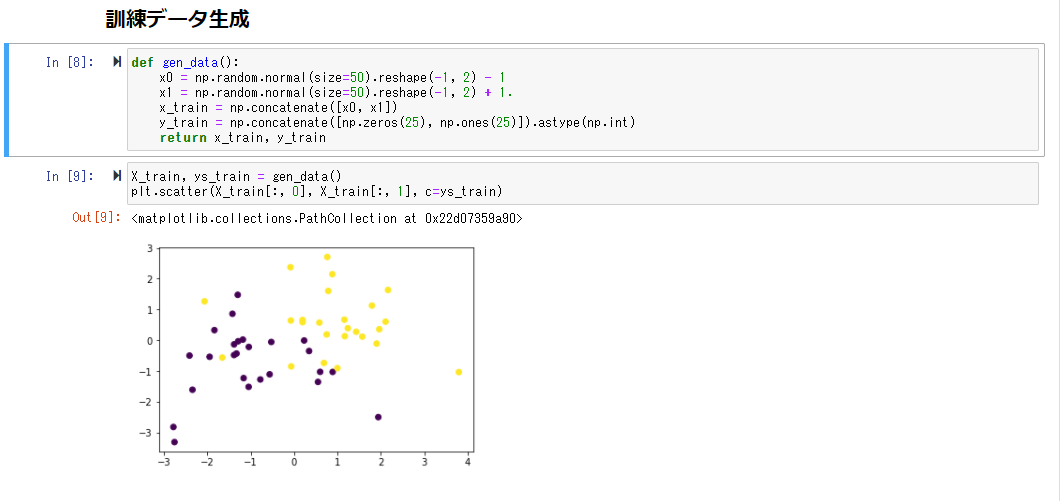
人口データと分類結果をプロットする

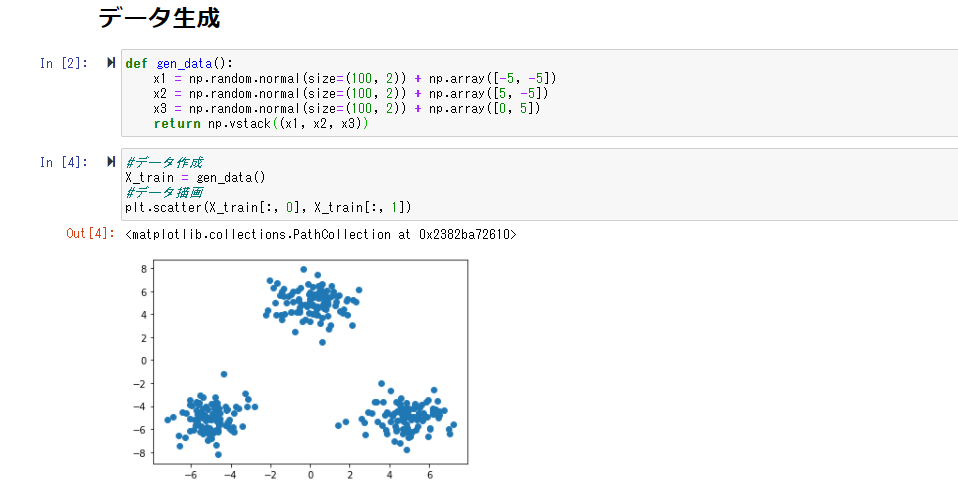
まずランダムなデータを作成すると、以下のような分布となった

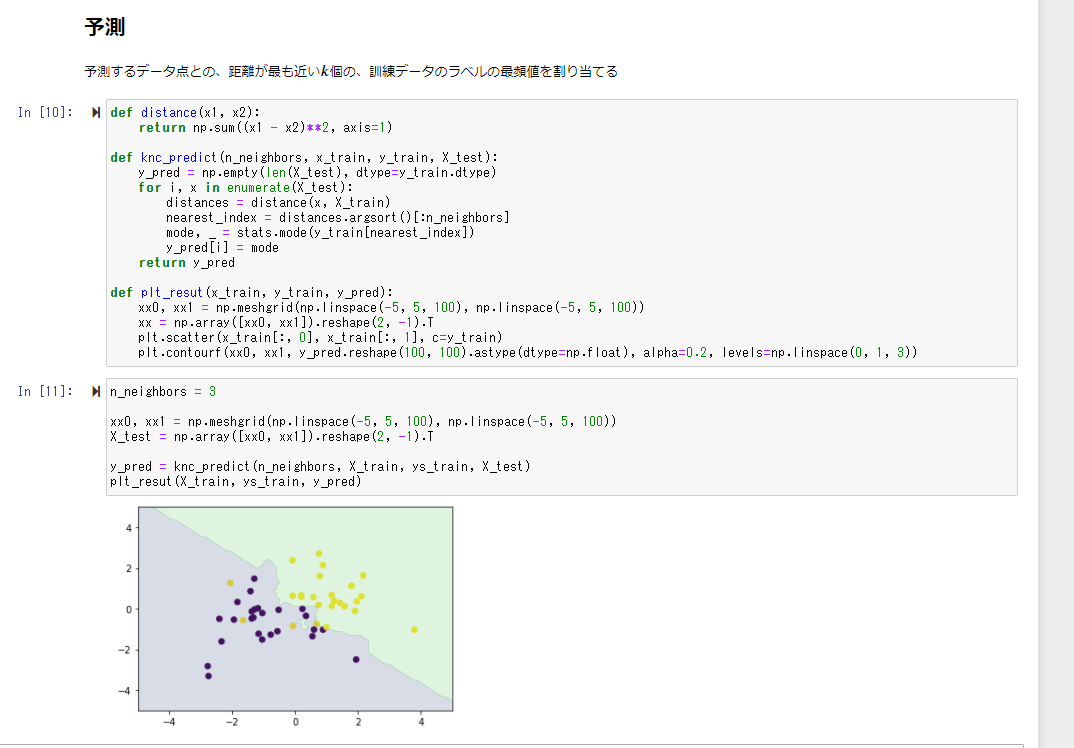
image.png

距離を求める関数、予測する関数、プロットする関数を作成し、

kを3として、numpyを用いて予測をしてみる

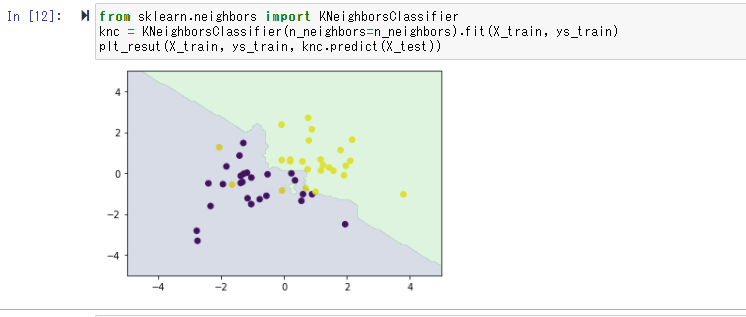
image.png

次にsklearnを用いて同様の処理を行う

image.png

同様の結果が出力されていることが確認できる

k平均法(k-means)

  • 教師無し学習
  • クラスタリング手法
  • 与えられたデータをk個のクラスタに分類する

中心の初期値にクラスタリングの結果が影響を受ける

⇒ k-means++という手法を用いることでこの問題は解決できる

ハンズオン

配布されているnotebookを実行してみる

まずクラスタリングしたいデータを作成する

image.png

次に以下の処理を実装、クラスタリングを行う

  1. 各クラスタ中心の初期値を設定する
  2. 各データ点に対して、各クラスタ中心との距離を計算し、最も距離が近いクラスタを割り当てる
  3. 各クラスタの平均ベクトル（中心）を計算する
  4. 収束するまで2, 3の処理を繰り返す

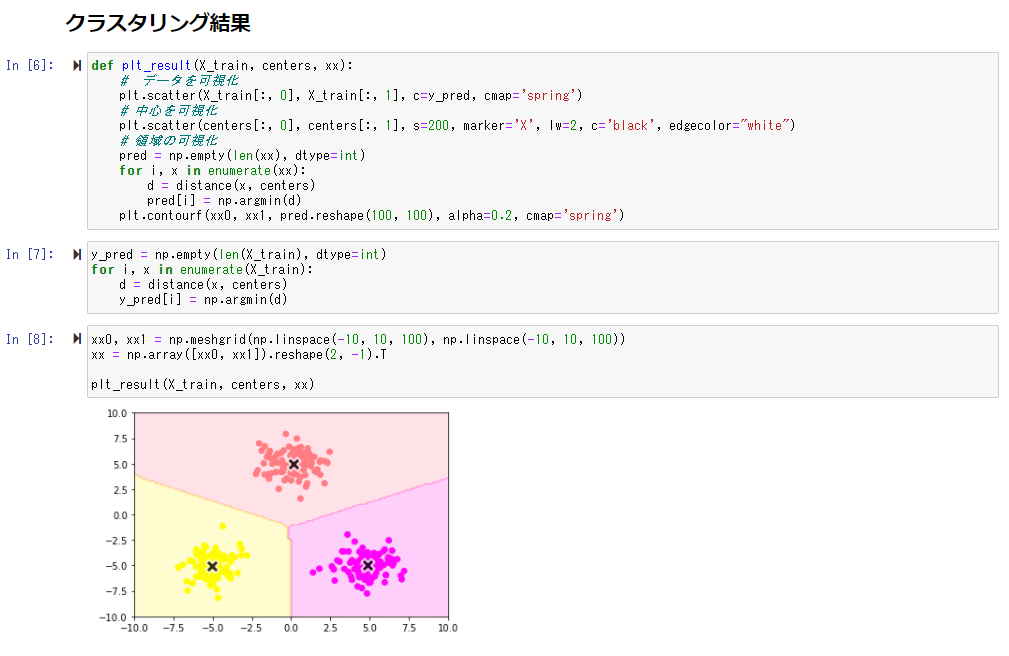
image.png

データ、領域、中心をそれぞれプロットする

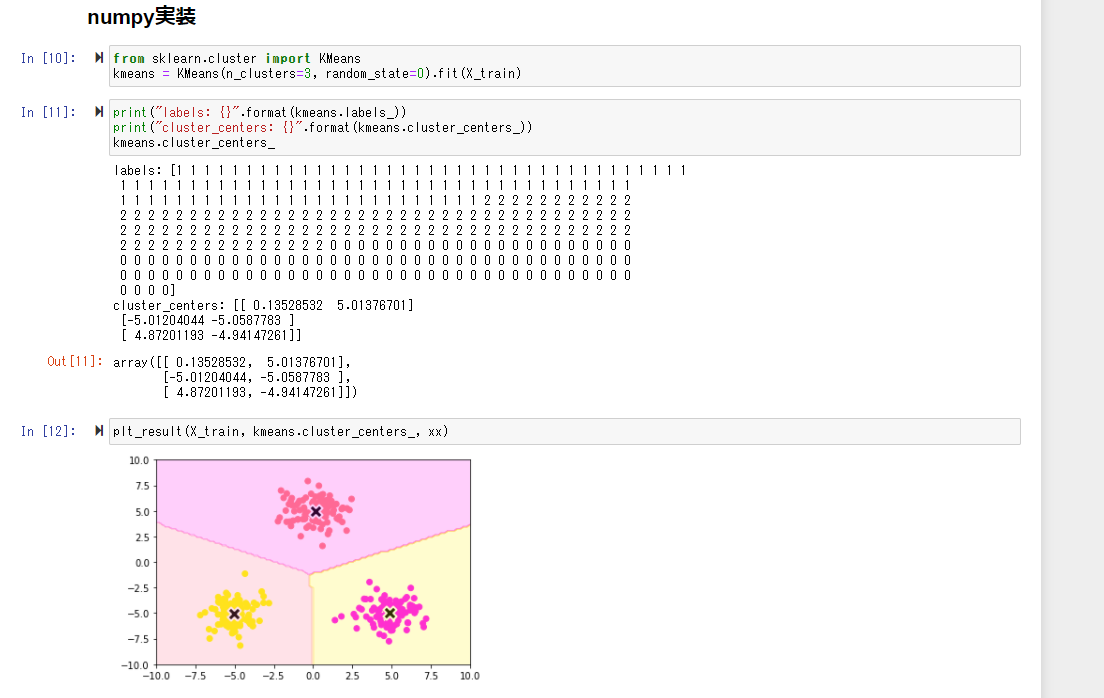
image.png

numpyでも同様の処理を実装する

image.png

同じような結果が出力されていることが確認できる

6.サポートベクターマシン(SVM)

2クラス分類のために利用される

線形モデルの正負で2値に分類できる

線形判別関数と最も近いデータ点との距離をマージンといい、これが最大になるものを求める

y = w^Tx + b = \sum_{j=1}^m w_ix_j + b

マージンを最大化することが目標であり目的関数は以下のようになり、

\max_{w,b}[\min_i \frac{t_i(w^Tx_i+b)}{||w||}]

さらに、マージン上の点において、$t_1(w^Tx_i+b) = 1$が成り立つため、以下のように変換できる

\max_{w,b} \frac{1}{||w||}

KKT条件

制約付き最適化問題において最適解が満たす条件

制約 $g_i(x) >=0(i=1,2…,n)$のもとで、$f(x)$が最小となる$x^*$は以下の条件を満たす

$\frac{theta L}{\theta x_j}|x^* = 0(j=1,2,…,n)$

$g_i(x^) <= 0, \lambda_i >= 0, \lambda_ig_i(x^) = 0 (i=0,1,…n)$

ラグランジュの未定乗数法

ラグランジュ関数 :$L(w,b,a) = \frac{1}{2}||w||^2 - \sum_{t=1}^n a_i (t_i(w^Tx_i +b)-1)$

$a_i > 0 (i=1,2,…,n)$はラグランジュ乗数である

そして最小となるw,bは以下を満たす

$\frac{\theta L}{\theta w} = w - \sum_{t=1}^n a_it_ix_i = 0$ => $w=\sum_{t=1}^n a_it_ix_i$

$\frac{\theta L}{\theta b} = - \sum_{t=1}^n a_it_i = 0$ => $\sum_{i=1}^n a_it_i = 0$

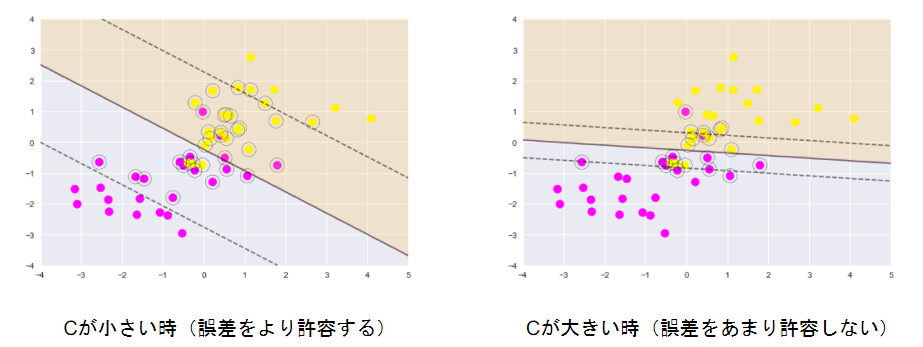
ソフトマージンSVM

サンプルを線形分離できないとき、誤差を許容し、誤差に対してペナルティを与える

目的関数: $\frac{1}{2}||w||^2 + C\sum_{t=1}^n \zeta_i$

制約条件: $t_i(w^Tx+b) >= 1 - \zeta_i(\zeta_i > 0)$

パラメータCの大小で決定境界が変化する

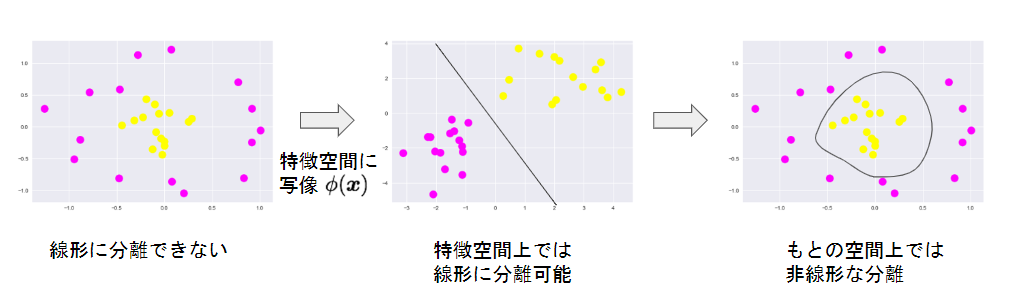
image.png

非線形分離

線形分離できない時、特徴空間に写像し、その空間で線形に分離する

image.png

ハンズオン

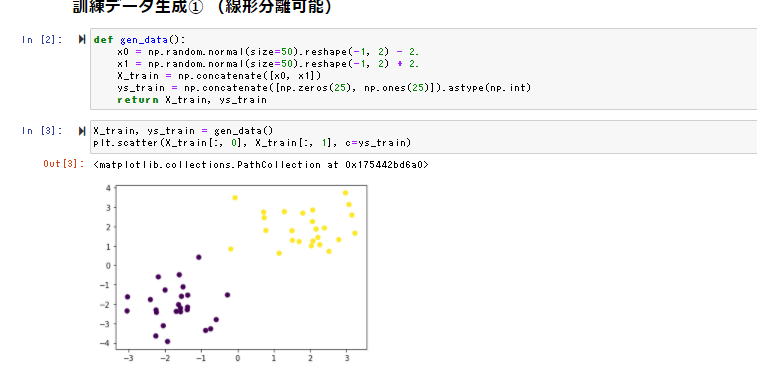
線形分離可能

データを作成

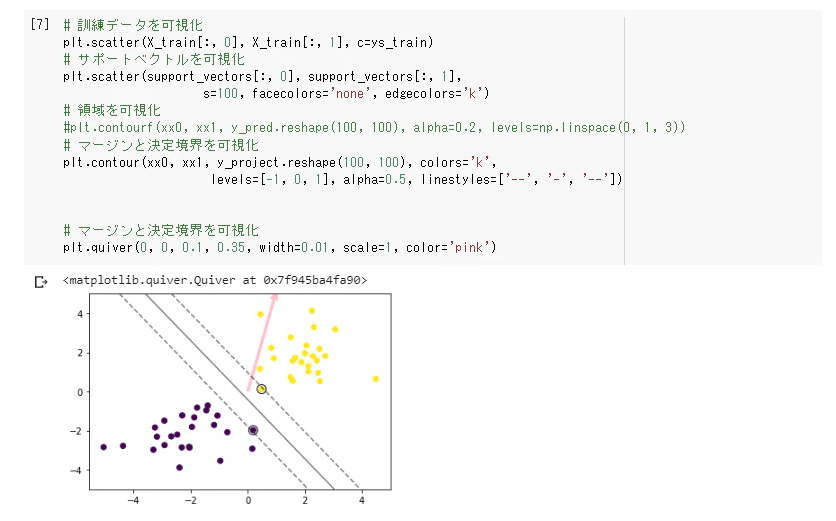
image.png

学習

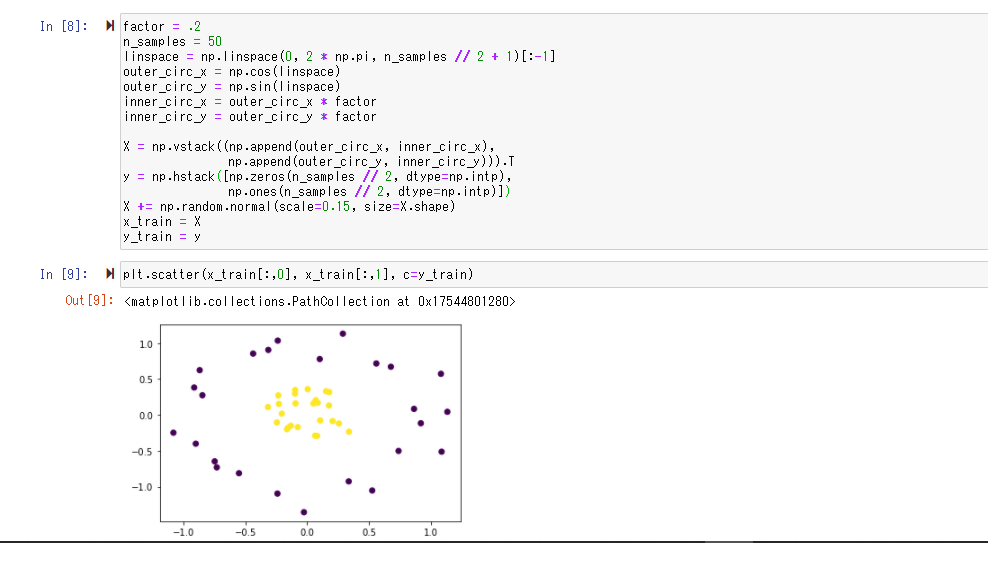
image.png

予測

image.png

image.png

線形分離不可

データ作成

image.png

学習

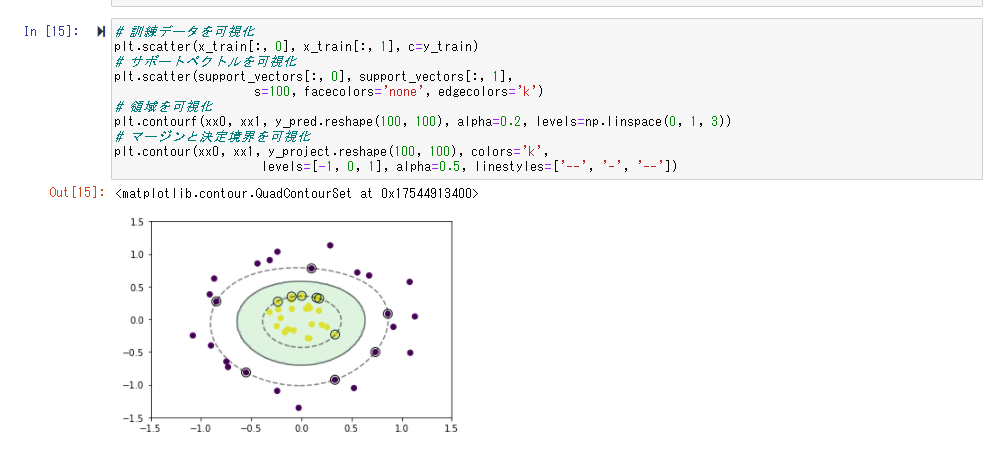
RBFカーネル(ガウネシアンカーネル)を利用する

image.png

予測

image.png

image.png

線形分離不可能なデータは特徴空間に落とし込むことで線形分離を行えることが確認できた

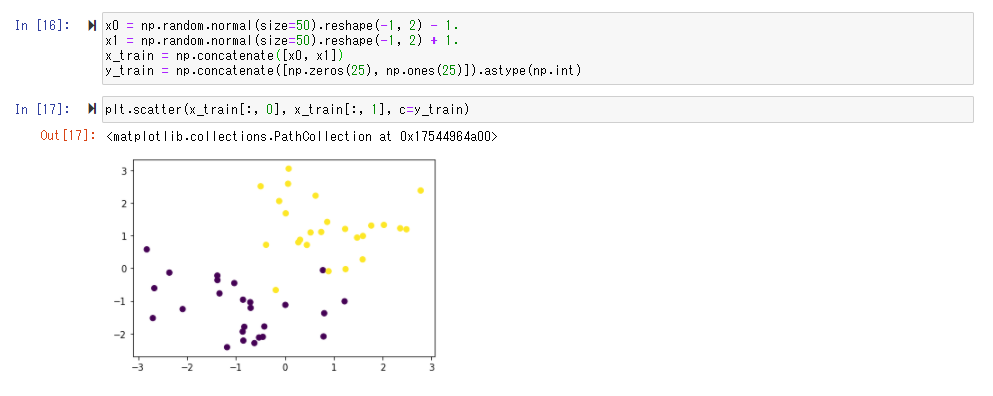
ソフトマージンSVM

データ作成

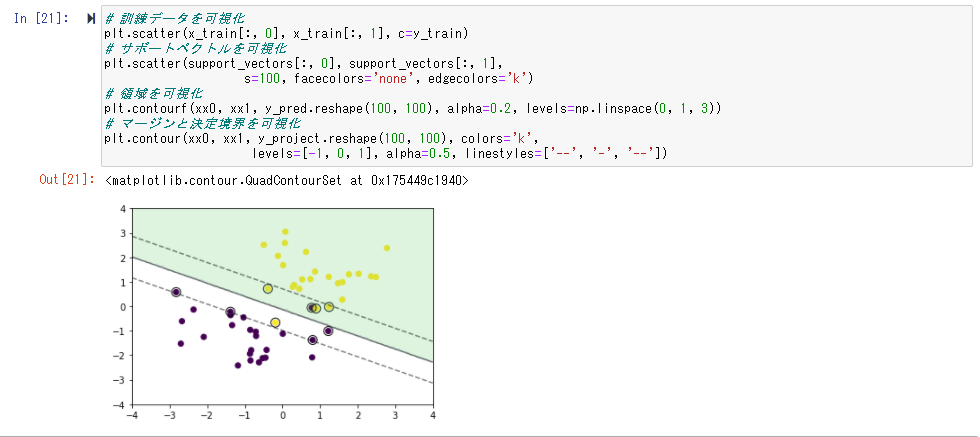
image.png

学習

image.png

予測

image.png

image.png

ソフトマージンSVMを使う事で、線形分離不可能な場合でも処理できることが確認できた

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?