統計学習の備忘録として、記事を書きました。今回はt分布・カイ二乗分布・F分布についてまとめました。関連する信頼区間の推定とF検定もまとめました。
t分布
母分散が未知でサイズの小さな標本から母平均などの推定・検定を行う場合に標準正規分布の代わりに用いる連続型の確率分布です。
t分布を説明する前にまず、標本平均$\bar x$に対してのz値についてみてます。
$$z_\bar x=\frac{\bar x -\mu}{\sqrt{\frac{\sigma^2}{n}}}$$
zは標準正規分布に従いますが、母分散$\sigma^2$がわかっていないと計算できません。現実的に母分散が明らかな場合は少ないです。そこで、この母分散$\sigma^2$を不偏分散${\hat{\sigma}}^2$で代用します。不偏分散とは、標本分散$s^2$の期待値が母分散に一致するように$\frac{n}{n-1}$をかけて調整した統計量です。$\frac{n}{n-1}$をかけるのは、nが十分に大きくないときは、標本分散の期待値は母分散よりも小さくなるためです。
$$t_\bar x=\frac{\bar x -\mu}{\sqrt{\frac{\hat\sigma^2}{n}}}=\frac{\bar x -\mu}{\sqrt{\frac{s^2}{n-1}}}$$
これがt値です。サイトなどによっては不偏分散で置き換えるのではなく、標本分散で置き換えているものもあります(下式)。
$$t_\bar x=\frac{\bar x -\mu}{\sqrt{\frac{s^2}{n}}}=\frac{\bar x -\mu}{\frac{s}{\sqrt{n}}}$$
ちなみに、$\frac{s}{\sqrt{n}}$は標本平均の標準誤差と言います。
そして、このt値は下記のような確率密度関数に従います。
$$f(t)=\frac{\Gamma((\nu+1) / 2)}{\sqrt{\nu \pi} \Gamma(\nu / 2)}\left(1+t^{2} / \nu\right)^{-(\nu+1) / 2}$$
$\nu$は自由度($n$-1)です。$\Gamma(\bullet)$はガンマ関数で、複素数を使った階乗を表す関数です。t分布は $\nu$によって形が変化します。
ここで、分布を実際に見てみましょう。
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
x = np.linspace(-6, 6, 1000)
fig, ax = plt.subplots(1,1, figsize=(10,7))
linestyles = [':', '--', '-.', '-']
deg_of_freedom = [1, 5, 30]
for df, ls in zip(deg_of_freedom, linestyles):
ax.plot(x, stats.t.pdf(x, df), linestyle=ls, label=f'df={df}')
ax.plot(x, stats.norm.pdf(x, 0, 1), linestyle='-', label='Standard Normal Distribution')
plt.xlim(-6, 6)
plt.ylim(0, 0.4)
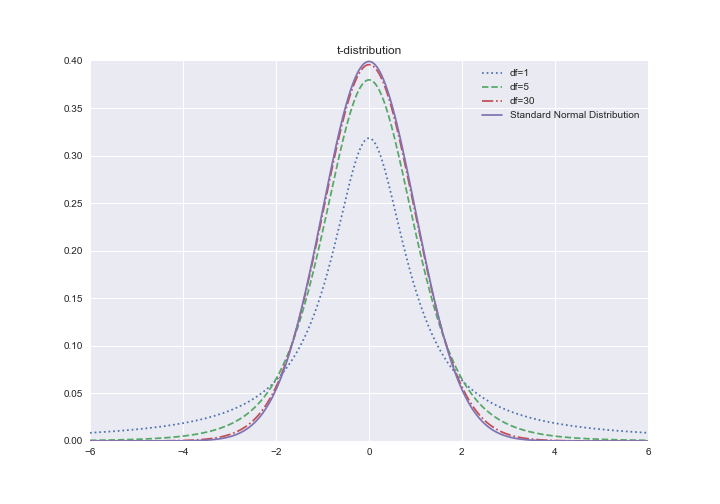
plt.title('t-distribution')
plt.legend()
plt.savefig('t-distribution.png')
plt.show()
自由度によって分布の形が変化していることがわかります。そして、標本サイズが大きいほど標準正規分布に近づいていることがわかります。
平均値の信頼区間の推定
この分布を使って母平均$\mu$が入ることを期待する信頼区間を推定してみます。
下記のようなデータが取れたとします。
data = [np.random.randn() for _ in range(10)]
print(data)
# >>> [-0.14917153222917484, 0.7951720064790415, 0.662152983830839, 0.430521357874449, -2.48235088848113, 0.6166315938744059, 1.055076432212844, 0.7400193126962409, 0.90477126838906, -0.10509107744284621]
print(f"標本平均:{np.mean(data)}")
# >>> 標本平均:0.24677314572037296
print(f"標本分散:{np.var(data)}")
# >>> 標本分散:0.9702146524752354
print(f"標本標準偏差:{np.sqrt(np.var(data))}")
# >>> 標本標準偏差:0.9849947474353533
このデータは標準正規分布に基づいて生成されているので、真の平均$\mu$は0になります。自由度が9、95%信頼区間の推定は、下記のような式変形で求めることができます。
$$-2.262≤t_{\bar x}≤2.262$$
$$-2.262≤\frac{\bar x-\mu}{\frac{s}{\sqrt{n-1}}}≤2.262$$
$$\bar x - 2.262\frac{s}{\sqrt{n-1}}≤\mu≤\bar x + 2.262\frac{s}{\sqrt{n-1}}$$
今回はデータが10と少ないので、不偏分散置換型で計算しました。また、2.262という数はt分布表から自由度9、2.5%の交差点の値を取ってきます。なので、標本平均が上記のデータは95%の確率で母平均が
bottom = np.mean(data) - 2.262*(np.sqrt(np.var(data))/(np.sqrt(len(data)-1)))
up = np.mean(data) + 2.262*(np.sqrt(np.var(data))/(np.sqrt(len(data)-1)))
print(f'{bottom} ≤ μ ≤ {up}')
# >>> -0.4959128938458835 ≤ μ ≤ 0.9894591852866295
ライブラリを使うと
bottom, up = stats.t.interval(alpha=0.95, loc=np.mean(data), scale=np.sqrt(np.var(data)/(len(data)-1)), df=len(data)-1)
print(f'{bottom} ≤ μ ≤ {up}')
# >>> -0.49596449533733994 ≤ μ ≤ 0.9895107867780859
のようになると推定できます。
カイ二乗分布
標本分散の分布など、複数の変数を一度に扱えるのがカイ二乗分布です。
まずカイ二乗値の定義を下記に示します。
$$\chi^2_{(n)}\equiv\sum^n_{i=1}z^2_i=\frac{\sum^n_{i=1}(x_i-\mu)^2}{\sigma^2}$$
$\chi^2$の下付きの$n$は自由度を表し母平均を基準としているため$自由度=n$としています。自由度が大きくなるとカイ二乗値も大きくなりやすくなっています。
そして、カイ二乗分布の確率密度関数は以下のようになります。
$$f(x ; k)=\frac{1}{2^{k / 2} \Gamma(k / 2)} x^{k / 2-1} e^{-x / 2}$$
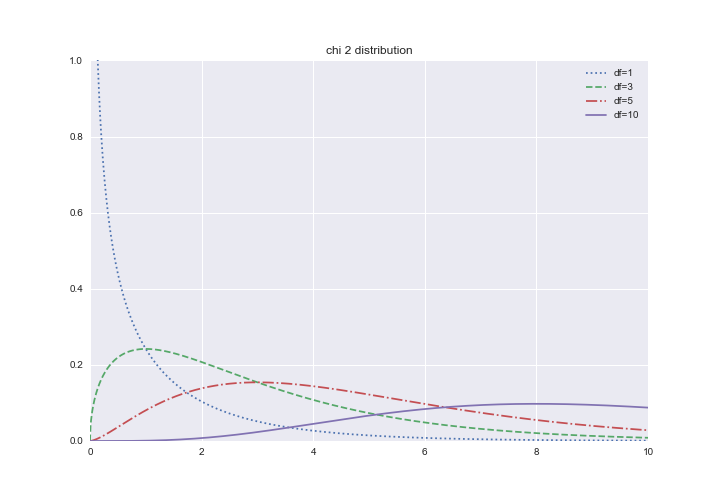
分布は以下のようになります。
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
x = np.linspace(0, 10, 1000)
fig,ax = plt.subplots(1,1, figsize=(10,7))
linestyles = [':', '--', '-.', '-']
deg_of_freedom = [1, 3, 5, 10]
for df, ls in zip(deg_of_freedom, linestyles):
ax.plot(x, stats.chi2.pdf(x, df), linestyle=ls, label=f'df={df}')
plt.xlim(0, 10)
plt.ylim(0, 1.0)
plt.title('chi 2 distribution')
plt.legend()
plt.savefig('chi2distribution.png')
plt.show()
母分散の区間推定
上記の式は母平均$\mu$だったので、標本平均$\bar x$で置き換えてみます。
$$\chi^2_{(n-1)}=\frac{\sum^n_{i=1}(x_i-\bar x)^2}{\sigma^2}$$
自由度はn-1しました。ここで、不偏分散$\hat \sigma^2$を使って表すと、
$$\chi^2_{(n-1)}=\frac{(n-1)\hat \sigma^2}{\sigma^2}$$
となり、$\chi^2$値が不偏分散と比例関係にあることがわかります。なので、母分散について解くと、
$$\sigma^2=\frac{(n-1)\hat \sigma^2}{\chi^2_{(n-1)}}$$
となるので、母分散の信頼区間を推定することができます。
データはt分布の時のものを使います。
data = [np.random.randn() for _ in range(10)]
print(data)
# >>> [-0.14917153222917484, 0.7951720064790415, 0.662152983830839, 0.430521357874449, -2.48235088848113, 0.6166315938744059, 1.055076432212844, 0.7400193126962409, 0.90477126838906, -0.10509107744284621]
print(f"標本平均:{np.mean(data)}")
# >>> 標本平均:0.24677314572037296
print(f"標本分散:{np.var(data)}")
# >>> 標本分散:0.9702146524752354
print(f"標本標準偏差:{np.sqrt(np.var(data))}")
# >>> 標本標準偏差:0.9849947474353533
自由度が9の時、信頼区間は以下のように計算できます。
$$\frac{(n-1)\hat \sigma^2}{\chi^2_{(n-1,\alpha/2)}}≤\sigma^2≤\frac{(n-1)\hat \sigma^2}{\chi^2_{(n-1,1-\alpha/2)}}$$
$$\frac{(n-1)\hat \sigma^2}{19.02}≤\sigma^2≤\frac{(n-1)\hat \sigma^2}{2.7}$$
よって、
bottom = ((len(data)-1)*np.var(data, ddof=1))/19.02
up = ((len(data)-1)*np.var(data, ddof=1))/2.7
print(f'{bottom} ≤ σ^2 ≤ {up}')
# >>> 0.5101023409438672 ≤ σ^2 ≤ 3.593387601760131
np.var(data, ddof=1))のddof=1とすることで不偏分散を求めています。
ライブラリを使うと、カイ二乗分布表の値を取得できます。
chi2_025, chi2_975 = stats.chi2.interval(alpha=0.95, df=len(data)-1)
bottom = ((len(data)-1)*np.var(data, ddof=1))/chi2_975
up = ((len(data)-1)*np.var(data, ddof=1))/chi2_025
print(f'{bottom} ≤ σ^2 ≤ {up}')
# >>> 0.5100281214306344 ≤ σ^2 ≤ 3.5928692971228506
F分布
F分布は、2つの母集団から無作為抽出した2つの標本に基づいた統計量が従う分布です。この性質を利用して、抽出元である2つの母集団の分散が同じかどうかを検定する際などに用いられます。
さて、F値に関してですが、F値は、正規分布に従う2つの母集団から無作為抽出してきた2つの$\chi^2$値の比です。正規分布に従うという点は重要です。
$$F_{(\nu_1, \nu_2)}=\frac{\chi^2_{(\nu_1)}/\nu_1}{\chi^2_{(\nu_2)}/\nu_2}$$
また、確率密度関数は以下のようになります。
$$f\left(x ; k_{1}, k_{2}\right)=\frac{\Gamma\left(\frac{k_{1}+k_{2}}{2}\right) x^{\frac{k_{1}-2}{2}}}{\Gamma\left(\frac{k_{1}}{2}\right) \Gamma\left(\frac{k_{2}}{2}\right)\left(1+\frac{k_{1}}{k_{2}} x\right)^{\frac{k_{1}+k_{2}}{2}}}\left(\frac{k_{1}}{k_{2}}\right)^{\frac{k_{1}}{2}}$$
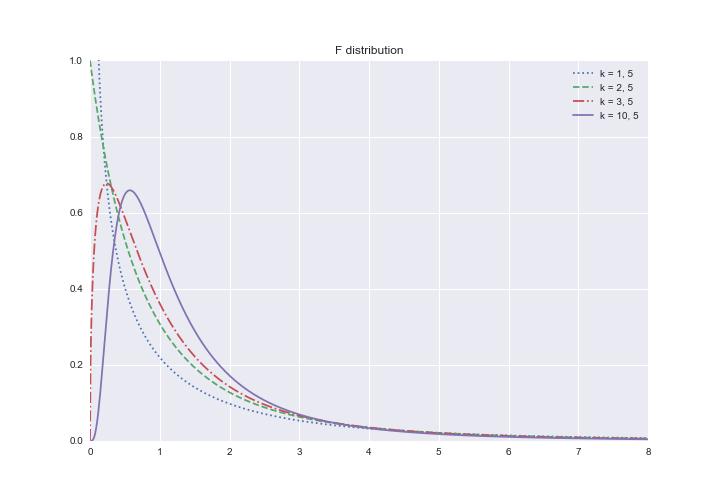
分布は以下のようになります。
F検定
F検定は2グループの分散に差があることを検定します。2グループの母分散($\sigma^2_1, \sigma^2_2$)が同じ場合F値は以下のようになります。
$$F=\frac{\chi^2_{(\nu_1)}/\nu_1}{\chi^2_{(\nu_2)}/\nu_2}=\frac{\frac{\nu_1\hat \sigma^2_1}{\sigma^2_1}/\nu_1}{\frac{\nu_2\hat \sigma^2_2}{\sigma^2_2}/\nu_2}=\frac{\hat \sigma^2_1}{\hat \sigma^2_2}$$
母分散が同じところから標本を抽出しているので、分散に差がなければ1に近づくはずです。逆にF値が1より大きい場合(普通分散が大きい方を分子とする)は、母分散は異なる可能性が高いです。
実際に検定してみます。
データは下記のようなデータを生成してみます。
# 日本人男性10人をサンプル
np.random.seed(1)
Japan = np.round([np.random.normal(64, 9, 10)],1).reshape(10)
jp_var = np.var(Japan, ddof=1)
# アメリカ人男性10人をサンプル
np.random.seed(1)
US = np.round([np.random.normal(87, 12, 10)],1).reshape(10)
us_var = np.var(US, ddof=1)
print(f'日本人の不偏分散:{jp_var}')
# >>> 日本人の標本分散:127.71955555555557
print(f'アメリカ人の不偏分散:{us_var}')
# >>> アメリカ人の標本分散:226.57377777777785
print(f'F値:{us_var/jp_var}')
# >>> F値:1.7739944113665709
F検定は
帰無仮説:2グループの分散は等しい
対立仮説:2グループの分散に差がある
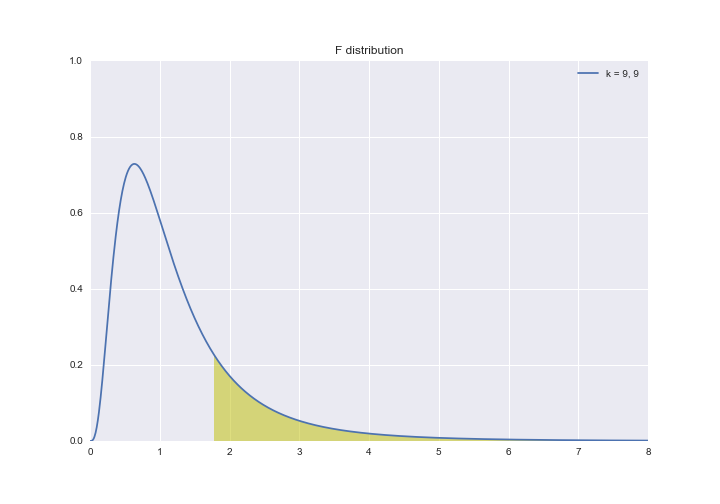
とします。自由度(9,9)のF分布で、下記のグラフの黄色い面積がp値にあたり、p値が0.05以下なら帰無仮説を棄却します。
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
x = np.linspace(0.000001, 8, 1000)
fig,ax = plt.subplots(1,1, figsize=(10,7))
df = (9,9)
ls = '-'
y = stats.f.pdf(x, df[0], df[1])
ax.plot(x, y, linestyle=ls, label=f'k = {df[0]}, {df[1]}')
plt.xlim(0, 8)
plt.ylim(0, 1.0)
plt.fill_between(x, y, 0, where=x>=us_var/jp_var, facecolor='y',alpha=0.5)
plt.title('F distribution')
plt.legend()
plt.savefig('fdistribution_p.png')
print(f'p-value:{stats.f.sf(us_var/jp_var, len(Japan)-1, len(US)-1)}')
# >>> p-value:0.20301975133837194
plt.show()
p値が0.203...で0.05より大きく帰無仮説は棄却できないので、2グループの分散に差があるとは言えなそうです。