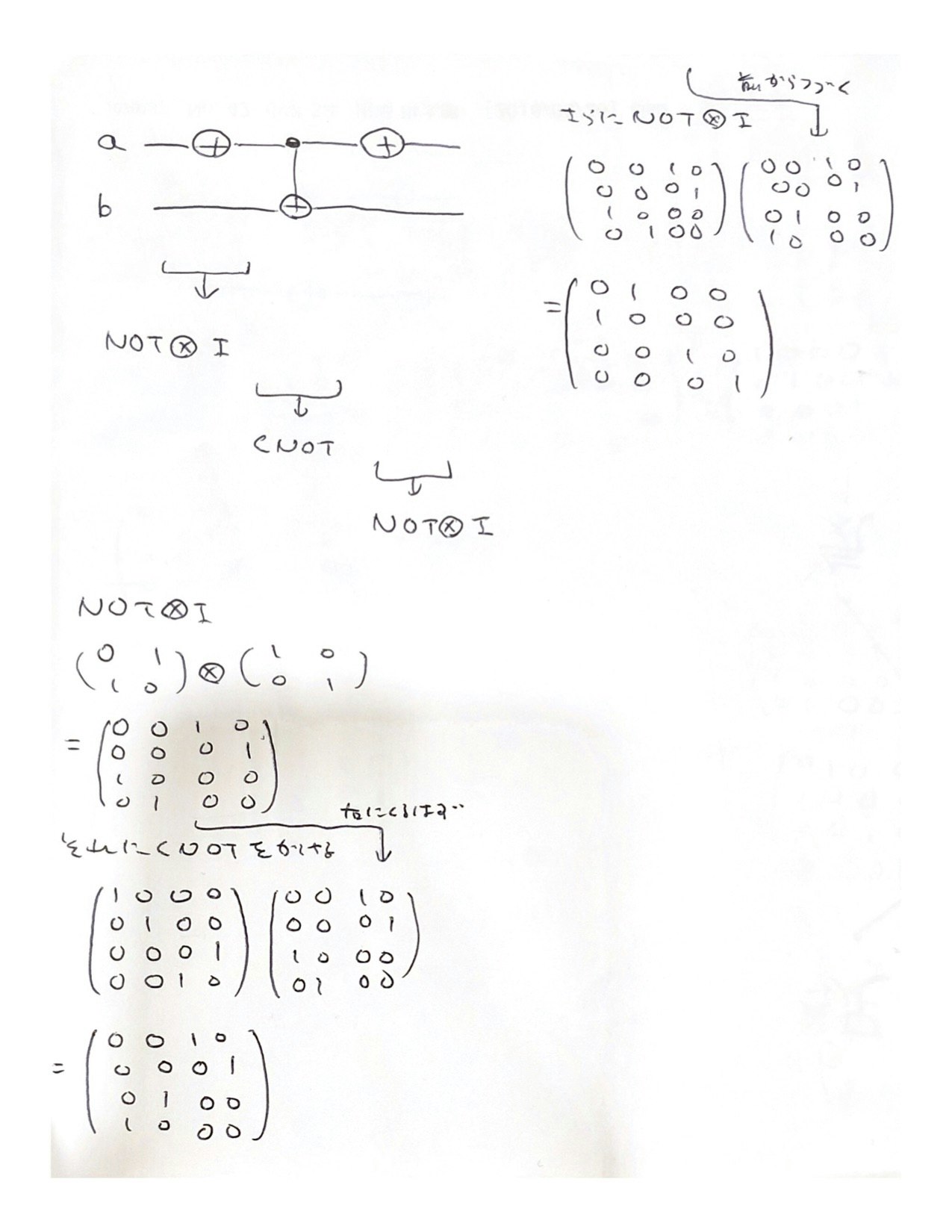今回は
前回に続き、量子コンピュータの講座を読み解いていこうと思います。
今回に限らず、タイトルで「旅立ち前夜」をうたっているように自分の理解もまだまだです。それでもこのシリーズを通じて自分なりの理解を書いていき、ご意見を頂きながら理解を深めていければと思っています!
さて第2回について。前回はあくまで導入で、計算や概念はそれほどややこしくなかったですが、ここから2量子ビットの系を扱い始めます。
複数量子ビットがあり、かつそれらがもつれあう状態にあることにより古典コンピュータを上回る性能を出しうる、というのが量子コンピュータの強みですので、かかる強みがどこからくるのか、イメージを掴んでおくことは大事だと思います。ただややこしいのは概念が非常に抽象的でとっつきにくく、かつ、先生すらも間違える点(ちなみに先生はよく間違えます)。以下、参考になりそうな書籍等にも触れながら読み解いていきます。
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
Tensor products and separable quantum states
このコマは何度も見ました。理由は3つあって、1)先生が結構間違えている 2)その割に重要な概念が続々出てきて、話題が飛ぶことに戸惑う 3)重要な概念が抽象的でとっつきにくい というのがあるためです。
自由度(degree of freedom)の議論が出てきますが、板書の書き間違いが多く混乱をきたしますのでご注意ください。
受講者の掲示板があるのですが、そちらによると、n量子ビットの系の自由度は、$2^{n+1}-2$です(板書では$2^n-2$)。
順に行きます。上式を使えば1量子ビットの自由度は$2$。当初黒板には「3」と書かれますが、これはのちに訂正されます。2つの基底ベクトルの係数がそれぞれ複素数なので、実数2つ分ずつ自由度があります。これで合計4つの自由度。一方規格化の条件(係数の2乗の和が1になる)が制約になるので自由度は1つ減ります。これで3。このイメージでショア先生は最初自由度を「$3$」としていたのだと思われます。ところが話はこれで終わりではなくて、グローバルの位相が変わっても状態は同じというのがあったので、その項をくくりだしてしまうと最後には2つの係数だけが残りますので、これで自由度が2ということになります。数式を使った考察についてはたとえばこちらをご覧ください。
間違いに気づいたショア先生は、「ブロッホ球の表面のどこかだから自由度は2」と訂正。シンプルな言い回しながら、確かに表面のどこかということであれば2つの角度で決まるので、自由度は2となります。これは直感的に捉えやすい説明と思いました。
続いて2量子ビットの場合です。この場合は、それぞれの量子ビットが$\ket{0}$と$\ket{1}$を取れるので、基底ベクトルは4つ。4つの係数は複素数なのでそれぞれ自由度が2ずつあるので8からスタート。ここから規格化条件で自由度が1つ減って、前述のとおりグローバル位相は状態に影響ないのでもう1つ減って、都合6つの自由度となります。
ここからの話が大事なところです。自由度が2の量子ビットを2つ持ってきたら自由度は4のはず。それなのに2量子ビットの系は自由度6とはこれいかに。これは、2量子ビットから構成される系の状態のうち、2つの量子ビットの状態に分解(factor into two things) できない 状態があることを指します。separable quantum statesとは、2量子ビットがそれぞれてんでの状態をとり、そのテンソル積として分解して記述できる状態(状態たち。states)のこと。この場合は自由度はそれぞれ2が2つ分。ところが先程の自由度6のほうが大きい。この差が、テンソル積に分解できない状態、言い換えれば2つの量子ビットが相関している状態であって、これがentangled state(日本語でいうともつれ合い)になります。後ほど練習問題で、どれがエンタングルしているかどうかを答えるものがありますが、その解き方がこれに当たります。つまり、2量子ビットの状態に分解可能なものはエンタングルしていないというわけです。
ちなみに、この回のレクチャーの題目にはseparableという表現があり、冒頭にdistinguishableという表現が使われています。似た言葉?と思うのですが、このseparableは複数量子ビットからなる状態を、ここの量子ビットのテンソル積に分解(separate)できる、という意味のようです。つまりエンタングルしている状態はseparableでないというわけです。
エンタングルメントについてはこのあとも何度も出てくるので今の段階で深く見ておく必要はないと思いますが、私が見た中でとても丁寧な説明だと思ったのは下記佐藤文隆先生の量子論の本 96ページあたりの説明がわかりやすいです。
そして、(ここでは)2つの量子ビットのそれぞれの状態を記述するのを、テンソル積として初めて説明しているセッションでもあります。行列表示も出てきていないのであくまでサラッとですので、手を動かすのはこれから。。
The no-cloning theorem
「(量子状態の)クローンを作る」からと言って、1つの量子ビットの状態を2つの量子ビットにコピーすると、次元数2の状態から次元数4の状態になり、具合が悪いことになります。そこで$\ket{0}$の状態の量子ビットを追加して(レジスタ)次元数をあわせます。このように仕切り直した上で、ある未知の状態$\ket\psi$と$\ket{0}$の量子ビットを使ったときに、$\ket{\psi}$の状態の量子ビット2つにできるかどうか、というお話です。(結論からいうとこれはできない)
同じく$\ket{\phi}$という状態をコピーできるかというとできない。その証明ですが、ユニタリー変換をしても内積が維持されるという性質を使う、、といっているのですがどうこの性質が活かされているかわからず。。これ自体の証明はなしにここでは使っています。$\ket{\psi}$$\ket{0}$と$\ket{\phi}$$\ket{0}$の内積を取ると、$\braket{\psi}{\phi}\braket{0}{0}$になります。で、仮に上記のクローンが作れるとすると、$\braket{\psi}{\phi}\braket{0}{0} = \braket{\psi}{\phi}\braket{\psi}{\phi}$ということになります。$\braket{0}{0}$は1ですから、$x = x^2$となります。これを解くと$x$は0か1。
読み取り方が難しいのですが、もし$\ket{\psi}$と$\ket{\phi}$がdistinguishable、つまり直交した独立の2つの状態(この場合$x=0$)のときにはコピーは作れる(測定を行って2つの基底状態のどちらかわかっているのでそれを使う)。2つの状態が同じなら(この場合$x=1$)、これもコピーできる(っていうかすでに同じ状態が2つあるということがすでにわかっている)。式が成り立つのはこの2パターンの特殊事例のみであって、このいずれとも違うより一般的なパターン、つまり未知の量子状態が2つ重ね合わさっているとこの式は成り立たず、未知の量子状態をコピーできないということになります。
ここでdistinguishableという表現がされていますが、少し前のTensor products and separable quantum statesの冒頭でdistinguishable spaceという表現をつかっているのを思い出すとイメージがわくとおもいます。これは例えば2量子ビットなら00,01,10,11などの基底状態を指し、1つ目の量子ビットを計測すれば1つ目と3つ目の基底状態が区別(distinguish)できるし、同じく2つ目の量子ビットを計測すれば2つ目と4つ目が区別できる、ということになります。
Tensor products of vectors - brief recap
先生の講義が早すぎて全然わからないので、別の所で調べたほうが早いです。たとえばこちら。
すごくざっくりとした捉え方としては、テンソル積印の左側のベクトル(行列でもよいのですが)のそれぞれの要素に、右側のベクトルや行列をまるっとかけていくような計算になります。それを上記の資料ではわかりやすく説明してくれているので参考になります。
Tensor products of matrices
行列のテンソル積の計算の仕方。この講座の中で最も重要と言っても過言ではないと思います。とはいえこれについても上で紹介したところのやり方のほうが理解しやすいです。ここからさき練習問題で何度も出てくるので、このコマの内容を頭に入れておくと良いかと思います。
A tensor product state in the Hadamard basis
$\ket{0}$ $\ket{1}$ で表記されるエンタングルした状態を、$\ket{+}$ $\ket{-}$ の基底で見てみるとどうなるか?という問い。アダマールゲート2つ($H \otimes H$) を作用させた結果を見ることになります。なぜかというと、アダマールゲートは$\ket{0}$から$\ket{+}$へと基底を置き換える操作をしてくれるからです。
具体的な計算ですが、先に計算していた4x4の行列を使って計算しています。結果として、$\ket{+}$ $\ket{-}$ の基底で見てもエンタングルしているということが確認されます。
4X4の行列を使うだけでなく、直接ケットベクトルを開いて計算するやり方もやっています。これは結構わかりやすくて、エンタングルした状態の中で01となっていればこのゼロを+に変換して、1をーに変換して、として計算するものです。この講義のシリーズ(Quantum Information Science I, Part 1)が終わったあと、第2シーズンの冒頭でこの辺の計算が再度出てきますので、覚えておくと良いです。
質問のところで、学生から、掛け合わせる行列はテンソル積である必要はあるか?との質問が出ています。答えはNoで、ユニタリーである必要はあるけれどもテンソル積である必要はないという回答になっています。そして、むしろ全部テンソル積だと量子コンピュータが成り立たないとも。この回答が意図するところは、掛け合わせるものが全部テンソル積だと、それぞれの量子ビットがてんでバラバラに動くだけなので、量子ビット同士が相互に連携することがなくなります(エンタングルもしなくなっちゃう、ということもあるのでしょう)。とすると量子計算が成り立たないという回答。深い回答ですが、そもそも深い質問でさすがです。
Gates for quantum circuits
ここは特にひねりはないので素直に講義を聞けば良いと思います。講義では出てきませんがあとで別のところで関係するCNOTの表現として、外積をつかって
\ket{0}\bra{0} \otimes I + \ket{1}\bra{1}\otimes X
と表現するやり方があります。これをどこかで思い出すと良いと思います。
CQ: Matrix description of quantum circuit
第1量子ビット側にNOTゲート 、次にCNOT、その後に再びNOTゲートという構成になっています。
ステップが3つあるので3つの行列の積を考えるやり方と、始状態(00,01,10,11)が3つのステップを経てどうなるかを書いて、それを行列で表すやり方をやってみました。結果は模範解答に一致しましたので大丈夫と思います。
解法1はこんな感じだと思います。行列表記に慣れていないので自分自身なかなか思い浮かばなかったのですが、1ステップ目はNOTゲートと単位行列のテンソル積になります。第1,第2量子ビットはそれぞれ別個に動くのでテンソル積で表現できるし、ゲートが作用するのは第1量子ビットだけだからです。それを順番にやっていくのですが、回路図で左から右に移動していくのをベクトルの積で表現することになるので、右側から順番にかけていくことになるはずです。(わかりにくくてすいません、左下から右上に続きます)
もう一つのやり方は上述の通り全パターンを網羅するやりかた。先生が講義でやっているやり方はこちらに近いですね。
続けていきます。