本記事の元ネタの「幅優先探索とビームサーチでWater Jug Problemを解いてみた」は、Water Jug Problemという馴染みがあって理解しやすい問題をプログラムで解いていくという素晴らしい記事なのですけど、コードを見てみると、なんだか私の知っているビーム・サーチと違う。というわけで、私の知っているビーム・サーチと、あと、元ネタの解法に近い(と思う)最良優先探索を実装してみました。
(2019年11月1日追記)
元ネタの方が記事を修正してくださいました。本稿で「元ネタのビーム・サーチ」と呼んでいる部分は、修正後の元ネタの最良優先探索の部分です。本稿は、RustのサンプルやC++17のサンプルを見たい場合や、冗長でもよいから詳しく説明して欲しいという場合にご利用ください。
実行方法
作成したプログラム(プログラミング言語はRust)はGitHubにあります。以下の手順で実行してみてください。
- 未インストールなら、GitとRustをインストールする
git clone https://github.com/tail-island/water-jug-problem.gitcd water-jug-problemcargo run --release
#一応、C++版も作りました。
#https://github.com/tail-island/water-jug-problem-cpp
私の知っているビーム・サーチ
私のへなちょこな英語力でWikipedia英語版のBeam searchを読んでみたら、以下のようなことが書かれていました(多分)。
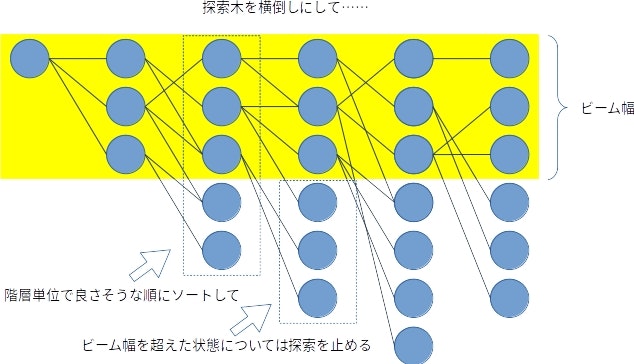
ビーム・サーチでは、幅優先探索と同様に探索木を構築する。探索木のそれぞれの階層で現在の階層に含まれる状態からすべての次の階層の状態を生成し、そして、ヒューリスティックで求めたコストが小さい順にソートする。生成した次の階層の状態は、良い方から順に、事前に定義したβ個(ビーム幅と呼ぶ)しか保持しない。その保持した状態からのみ、さらに次の階層の状態を生成していく。
私の理解を図にすると、こんな感じ。
つまり、私の理解だと、ビーム幅ってのは探索木の階層単位での幅なんです。
元ネタのビーム・サーチ
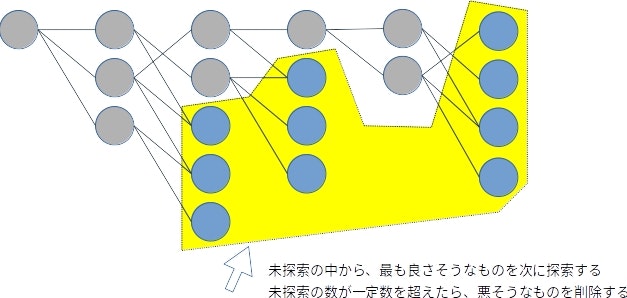
元ネタでは、階層は無関係で、未探査の探索木のノードの数が指定した数を超えないようにしています。図にすると、こんな感じ。
このアルゴリズムは、私には足切りを追加した最良優先探索に見えます。本稿では最良優先探索も作成してみますので、確認してみてください。
今回扱う問題
元ネタと同じ問題を使います。
ユウキ君は8dLのピッチャーに入ったヨーグルトスムージーをレイちゃんと半分にする方法を考えています。
ユウキ君は8dL、5dL、3dL入るピッチャーを使うことができます。
スムージーを最低何回移し替えればいいでしょうか?
この問題のルールを、最近勉強しているので使いたくてしょうがないRustで実装したら、以下のようになりました。
use std::cmp::*;
use std::iter::*;
use itertools::iproduct;
// ゲーム。今回は、ピッチャーの容量の集合。
pub struct Game {
pitcher_capacities: Vec<i32>
}
// 状態。今回は、ピッチャーに入っているヨーグルト・スムージーの量の集合。
# [derive(Clone, Eq, Hash, PartialEq)]
pub struct State {
pitchers: Vec<i32>
}
// 手。今回は、移動元と移動先のピッチャーのインデックス。実装が面倒だったので、型エイリアスで。
pub type Action = (usize, usize);
impl Game {
// 新しいゲームを作成します。
pub fn new(pitcher_capacities: &[i32]) -> Game {
Game {
pitcher_capacities: pitcher_capacities.to_vec()
}
}
// ピッチャーの容量の集合を取得します。
pub fn pitcher_capacities(&self) -> &Vec<i32> {
&self.pitcher_capacities
}
// 初期状態を取得します。
pub fn initial_state(&self) -> State {
State {
pitchers: self.pitcher_capacities.iter().take(1).copied().chain(repeat(0)).take(self.pitcher_capacities.len()).collect() // 最初のピッチャーはいっぱい、他は空。
}
}
// 合法手一覧を取得します。
pub fn legal_actions(&self, state: &State) -> Vec<Action> {
iproduct!(0..self.pitcher_capacities.len(), 0..self.pitcher_capacities.len()).filter(|&(f, t)| {
f != t && state.pitchers[f] != 0 && state.pitchers[t] != self.pitcher_capacities[t] // ピッチャーが異なっていて、移動元が空でなくて、移動先がいっぱいでないなら、合法。
}).collect()
}
// 次の状態(stateにactionを実行した結果)を取得します。
pub fn next_state(&self, state: &State, action: &Action) -> State {
let mut next_pitchers = state.pitchers.clone();
let &(f, t) = action;
next_pitchers[f] = max(state.pitchers[f] - (self.pitcher_capacities[t] - state.pitchers[t]), 0);
next_pitchers[t] = min(state.pitchers[t] + state.pitchers[f], self.pitcher_capacities[t]);
State {
pitchers: next_pitchers
}
}
// ゴールに到達したかチェックします。
pub fn is_goal(&self, state: &State) -> bool {
state.pitchers.iter().any(|&pitcher| pitcher == self.pitcher_capacities[0] / 2) // 最初のピッチャーのサイズの半分のピッチャーがあるなら、はんぶんこ成功!
}
}
impl State {
// ピッチャーに入っているヨーグルト・スムージーの量の集合を取得します。
pub fn pitchers(&self) -> &Vec<i32> {
&self.pitchers
}
}
問題そのものをゲーム(Game)、ゲームを進めていく中で変わっていく状態(State)、状態を変えるアクション(Action)に分割しました。ルールを表現するメソッドの実装は、元ネタのままです(legal_actions()メソッドの、移動元移動先の処理だけ追加)。
さて、このコードは冗長に感じるかもしれません。ですが、この程度にでも抽象化しておくと、探索処理の作成がとても容易になるんです。それを証明するために、ランダムで適当に探索するプログラムを作ってみました。そのコードは、こんな感じ。
use rand::*;
use rand::seq::*;
use super::game::*;
pub fn answer(game: &Game) -> Option<Vec<Action>> {
// ランダム・ナンバー・ジェネレーター。
let mut rng = thread_rng();
// 初期状態を取得します。
let mut state = game.initial_state();
// 解答の入れ物を作成します。
let mut answer = Vec::new();
// 10000回ほど……
for _ in 0..10000 {
// 合法手の中からランダムで一つ手を選んで、
let action = game.legal_actions(&state).into_iter().choose(&mut rng).unwrap();
// 次の状態に遷移します。
state = game.next_state(&state, &action);
// 解答も作成します。
answer.push(action);
// もしゴールなら、解答をリターンします。
if game.is_goal(&state) {
return Some(answer);
}
// ゴールでないなら、処理を繰り返します。
}
// 正解が見つからない場合は、Noneを返します。
None
}
ほら、コードがとても単純です。あと、ゲームの内容が変わっても、このコードはそのまま使えるでしょ?
とはいえ、正しく動作しないのでは意味がありませんから、上のコードが正しく動くか確かめてみましょう。
use water_jug_problem::game::*;
use water_jug_problem::random_search;
// 解答出力。
fn print_answer(game: &Game, answer: &[Action]) {
let mut state = game.initial_state();
for action in answer {
state = game.next_state(&state, &action);
println!("{:?}, {:?}", action, state.pitchers());
}
}
// メイン・ルーチン。
fn main() {
// 8dL、5dL、3dLのピッチャーで問題を作成して、
let game = Game::new(&[8, 5, 3]);
// ランダム・サーチで解いてみます。
if let Some(answer) = random_search::answer(&game) {
print_answer(&game, &answer);
} else {
println!("no answer...");
}
}
(0, 2), [5, 0, 3]
(2, 1), [5, 3, 0]
(1, 2), [5, 0, 3]
(省略)
(1, 2), [6, 0, 2]
(0, 1), [1, 5, 2]
(1, 2), [1, 4, 3]
左側がアクション(どのピッチャーからどのピッチャーへ移すのか)、右側が状態(各ピッチャーに入っているヨーグルト・スムージーの量)です。最後の行で2つめのピッチャーが4dLになっているので、はんぶんこは成功ですね。はい、これで、ゲームのルールの実装は完了しました。
幅優先探索
でも、先程のランダム・サーチの解答は、なんだかあまりにひどい。長すぎますし、実は何度も初期状態まで戻ったりしています。もっと短い手数ではんぶんこする素敵な解答があるはず。というわけで、最短手数の解答を見つけてくれる、幅優先探索を作成してみましょう。
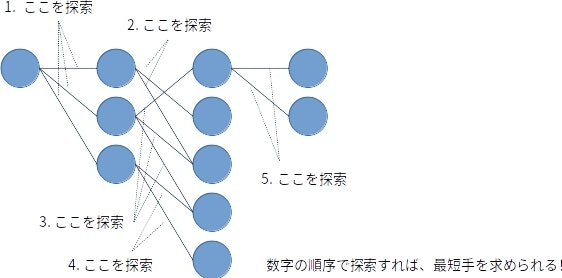
さて、ランダム・サーチの問題点は、たくさんある合法手の中からたった一つだけを選んで、残りは試さないことだと考えます。残りも試せば、具体的には合法手1を試した結果、合法手2……とすべての合法手を試してみて、で、まだゴールできていないなら合法手1を試した結果の状態での合法手すべててで同じことをして、合法手2を試した結果の状態での合法手すべてで……という順でやっていくなら、最短手数の解答を導けるはずです。
で、上で書いたアルゴリズムをそのまま実装してもよいのですけど、これ、「合法手を試した結果の状態を、順序を保って処理する」とやるだけでも結果は同じになりますよね? 順序を保てば、階層の順序も自ずと守られますから。で、コンピューターで順序を保って処理したい場合は、先入れ先出し(先に入れたものが先に出てくる)を実現してくれる「キュー」を使うのが定石です。というわけで、幅優先探索のコードは、以下のようになります。
use std::collections::*;
use super::game::*;
// 次の解答を取得します。clone()してpush()するだけでもよいのですけど、少しだけ、メモリ効率を考えてみました。
fn next_answer(answer: &[Action], action: &Action) -> Vec<Action> {
let mut result = Vec::with_capacity(answer.len() + 1);
result.extend_from_slice(answer);
result.push(action.clone());
result
}
// 幅優先探索。
pub fn answer(game: &Game) -> Option<Vec<Action>> {
// ノード。状態と、その状態に至る解答です。
struct Node {
state: State,
answer: Vec<Action>
}
// キューと探索済みの集合を管理するためのセットを作成します。
let mut queue = VecDeque::new();
let mut visited = HashSet::new();
// キューに初期状態を追加します。
queue.push_back(Node {
state: game.initial_state(),
answer: Vec::new()
});
// 初期状態を探索済みにしておきます。
visited.insert(game.initial_state());
// キューが空でなければ、処理を繰り返します。
while !queue.is_empty() {
// 次のノードを取得します。
let node = queue.pop_front().unwrap();
// 合法手すべてでて……
for action in game.legal_actions(&node.state) {
// 次の状態を取得します。
let next_state = game.next_state(&node.state, &action);
// 次の状態が探索済みでなければ……
if visited.insert(next_state.clone()) {
// 次の解答を取得します。
let next_answer = next_answer(&node.answer, &action);
// ゴールなら、その解答をリターンして終了します。
if game.is_goal(&next_state) {
return Some(next_answer);
}
// 新しいノードをキューに追加します。
queue.push_back(Node {
state: next_state,
answer: next_answer
});
}
}
}
// 正解が見つからない場合は、Noneを返します。
None
}
まずは、利便性と効率のためにnext_answer()関数を作成しました。幅優先探索ではすべての合法手を試さなければならないので、手を試す前のStateやanswerを残しておかなければなりません(そうしないと、次の手を同じ状態から試せませんもんね)。stateについてはnext_state()メソッドが新しい状態を作成して返すようになっているので問題ないのですけど、answerはどうしましょうか? 先程のランダム・サーチのように単純にanswerにpush()してしまうと、元のanswerは失われてしまいますもんね。というわけで、clone()してpush()しなければならないのですけど、Vec構造体では要素数が増えるときにメモリの再割当てが発生してパフォーマンスを損なう危険性があります。なので、少しだけ効率に考慮したnext_answer()関数を作成してみました。
コードの残り、実際に幅優先探索をするanswer()関数の説明に移りましょう。上のコードのように、Rustでキューを使いたい場合はVecDequeという構造体を使用します。あと、探索済みの状態で探索を続けても無意味なので、visitedに探索済みの状態を保存しておいて、未探索の場合にのみ処理するようにしています。このような処理は、上のコードのようにHashSetを使うと実装が容易です。あとはそう、元ネタではキューから取り出したあとで探索済みチェックやゴール・チェックをしていたのですけど、Wikipediaの幅優先探索の疑似コードにならって、キューに追加する前にこれらの処理を入れました。こちらのほうが処理が速いですもんね(初期状態がゴールになりえる場合、麻雀の天和みたいなのがある場合はダメですけど)。
というわけで、これで完成です。試してみましょう。
(0, 1), [3, 5, 0]
(1, 2), [3, 2, 3]
(2, 0), [6, 2, 0]
(1, 2), [6, 0, 2]
(0, 1), [1, 5, 2]
(1, 2), [1, 4, 3]
やりました。元ネタと同じ最適解が出ました。やっぱり幅優先探索は良いじゃん!
最良優先探索
でも、幅優先探索って無駄がありそうな気がします。たとえば迷路のゴールを目指して歩いているときに、ゴールから遠ざかる道よりはゴールに近づく道を先に試した方が良さそうですよね? でも、幅優先探索ではどちらの道も同様に扱わなければなりません……。というわけで、「良さ」を計算して、で、その「良さ」の順に探索をしようってのが最良優先探索です。無駄がなくて良さそうでしょ?
とはいっても、最適解を出せるかは「良さ」の精度次第なんですけどね。たとえば迷路なんかの場合は、スタートから現在位置までの歩数と、現在位置からゴールまでの歩数の予測値(ただし、実際のゴールまでの歩数以下でなければならない)を使うことで、最良優先探索で最短ルートを導けるんです(これがいわゆるA*)。実際のゴールまでの歩数よりも小さい、かつ、現在位置からゴールまでの歩数の予測値には、壁がない場合のゴールまでの歩数を使用しちゃえばオッケー。壁があるので、必ず実際の歩数は大きくなりますもんね。
でも、今回の問題だと、これまでに移し替えた回数は分かるけれど、正解に至るまでにこの先移し替える回数以下の、かつ、妥当な回数を計算する計算式なんか全く思いつきません。なので、最適解にはならないかもしれないけど、幅優先探索より短時間でそこそこの解答を出す手段としての最良優先探索になります。コードはこんな感じ。
use std::collections::*;
use std::cmp::*;
use super::game::*;
// 次の解答を取得します。clone()してpush()するだけでもよいのですけど、少しだけ、メモリ効率を考えてみました。
fn next_answer(answer: &[Action], action: &Action) -> Vec<Action> {
let mut result = Vec::with_capacity(answer.len() + 1);
result.extend_from_slice(answer);
result.push(action.clone());
result
}
// 評価関数。元ネタと同じ。ここが超絶凄ければ、最適解が出せます。そういえば、深層学習でゴールまでの手数を学習させてルービック・キューブを解くというのがあって面白かった。この問題も深層学習で精度を挙げられるかもしれないけど、誰かやってくれないかなぁ……
fn score(game: &Game, state: &State, answer: &[Action]) -> i32 {
let target = game.pitcher_capacities()[0] / 2;
-(answer.len() as i32) + state.pitchers().iter().fold(0, |acc, pitcher| acc + if pitcher % target == 0 { 10 } else { 0 } - (target - pitcher).abs())
}
// 最良優先探索。
pub fn answer(game: &Game) -> Option<Vec<Action>> {
// ノード。評価結果を入れるscoreを追加しました。
struct Node {
state: State,
answer: Vec<Action>,
score: i32
}
// BinaryHeap(priority queueが必要な場合はこれを使えとRustのドキュメントに書いてあった)で使えるように、PartialEqとEq、PartialOrd、Ordを実装します。
impl PartialEq for Node {
fn eq(&self, other: &Self) -> bool {
self.score == other.score
}
}
impl Eq for Node {}
impl PartialOrd for Node {
fn partial_cmp(&self, other: &Self) -> Option<Ordering> {
Some(self.cmp(&other))
}
}
impl Ord for Node {
fn cmp(&self, other: &Self) -> Ordering {
self.score.cmp(&other.score)
}
}
// 優先度付きキューと探索済みの集合を管理するためのセットを作成します。
let mut queue = BinaryHeap::new();
let mut visited = HashSet::new();
// キューに初期状態を追加します。
queue.push(Node {
state: game.initial_state(),
answer: Vec::new(),
score: 0
});
// 初期状態を探索済みにしておきます。
visited.insert(game.initial_state());
// キューが空でなければ、処理を繰り返します。
while !queue.is_empty() {
// 次のノードを取得します。
let node = queue.pop().unwrap();
// 合法手すべてでて……
for action in game.legal_actions(&node.state) {
// 次の状態を取得します。
let next_state = game.next_state(&node.state, &action);
// 次の状態が探索済みでなければ……
if visited.insert(next_state.clone()) {
// 次の解答を取得します。
let next_answer = next_answer(&node.answer, &action);
// ゴールなら、その解答をリターンして終了します。
if game.is_goal(&next_state) {
return Some(next_answer);
}
// 次のスコアを取得します。
let next_score = score(&game, &next_state, &next_answer);
// 新しいノードをキューに追加します。
queue.push(Node {
state: next_state,
answer: next_answer,
score: next_score
});
}
}
}
// 正解が見つからない場合は、Noneを返します。
None
}
なにはともあれ、「良さ」を評価する評価関数score()を作りました。内容は元ネタのまま。前半部分はこれまでの手数ですけど、後半は手数とは異なる単位の値なので大小関係が分かりません。だから最適解が出る保証はなし……。でも、現実の問題では、最良優先探索で最適解が出せる場合の方が少ないんだよ! A*は特殊例なんだよ! 元ネタの人はもちろん、私だって悪くないんだよ!
あと、「評価値が最も良いものから順に」の部分を手でソートしてやるのは面倒な上に遅そうなので、priority queueを使用しました。Rustのドキュメントを見たら、priority queueを使いたい場合はBinaryHeapを使えと書いてあったので、BinaryHeapを使用します(C++の場合はstd::priority_queueを使ってください)。RustのBinaryHeapは大きい順にソート(なので、いわゆるコストや損失ではなくてスコアになる)なのですけど、元ネタもcomp()関数で大きい順になるようにソートしていますから、先程の評価関数はこのままでよいはず。
というわけで、先程の幅優先探索のQueueをBinaryHeapに変更して、Nodeにスコアを追加してやるだけでよい……はずだったのですけど、RustでBinaryHeapを使う場合は同じ値かを調べたり大小比較ができることを保証しなければならないみたい。だから、NodeにPartialEqとEq、PartialOrd、Ordを実装するコードも追加になってしまいました。その部分を除けば、ほら、最良優先探索と幅優先探索とほぼ同じでしょ?
ともあれ、実行してみます。すると、元ネタと同じ解答が出ました。
(0, 2), [5, 0, 3]
(2, 1), [5, 3, 0]
(0, 2), [2, 3, 3]
(2, 1), [2, 5, 1]
(1, 0), [7, 0, 1]
(2, 1), [7, 1, 0]
(0, 2), [4, 1, 3]
あれ? 元ネタにはあった枝狩り処理がないのに同じ解答? どうして?
というものですね、元ネタのコードを動かしてみるとわかるのですけど、探索木が小さすぎるので元ネタの枝狩りする部分のコードは動いていないんですよ(printfデバッグで調べました)。評価関数が最適解ではない解を良いと主張したから、その解の方が先に処理されたというだけなんです(元ネタのループをbreakする部分でdequeの残りを出力してみれば、残りに最適解が入っていることがわかります)。
というわけで、たとえば評価関数を以下のように少し修正すれば、上の最良優先探索のコードは最適解を出力します。我ながらへっぽこな評価関数なので、たまたまうまくいっただけな気もしますけどね。
fn score(game: &Game, state: &State, answer: &[Action]) -> i32 {
let target = game.pitcher_capacities()[0] / 2;
-(answer.len() as i32) - (state.pitchers().iter().map(|pitcher| (target - pitcher).abs()).min().unwrap())
}
ともあれ、最良優先探索は作るの簡単なのに効率よさそうで良いじゃん!
ビーム・サーチ
でもね、最良優先探索では、探索木が大きい場合には膨大な時間がかかってしまうんですよ。良さそうな手なので少し進めてみたのだけどやっぱりそんなに良くなさそうなので戻って別の手を……と進んだり戻ったりすると、いつまでたっても先の局面まで進みません。ほら、現実的な時間では終わらなそうでしょ?
というわけで、探索木をバッサリと枝狩りしてしまいましょう。階層単位で、良さそうに思える一定数の状態を残して他は捨てちゃう。これなら、一定時間で必ず先に進みます。解に至る枝を削除してしまって答えが出ないかもしれませんし、最適解も出ないかもしれませんけど、いつまで待っても返ってこない答えを待つよりはるかにマシ。と、こんな少し乱暴な探索がビーム・サーチなんです。
で、この階層単位で一定数の状態しか保存しないってのをそのまま実装しても良いのですけど(状態をVecに入れてソートして後ろを削るとか)、最良優先探索で使用したpriority queueを2つ使用して、次の階層の状態をすべて保存するけど一定数しかpopしない、という実装にするととても簡単です。こんな感じ。
use std::collections::*;
use std::cmp::*;
use super::game::*;
// 次の解答を取得します。clone()してpush()するだけでもよいのですけど、少しだけ、メモリ効率を考えてみました。
fn next_answer(answer: &[Action], action: &Action) -> Vec<Action> {
let mut result = Vec::with_capacity(answer.len() + 1);
result.extend_from_slice(answer);
result.push(action.clone());
result
}
// 評価関数。同じ手数同士での比較なので、手数は評価に含めません。それ以外は、元ネタと同じ。
fn score(game: &Game, state: &State, _answer: &[Action]) -> i32 {
let target = game.pitcher_capacities()[0] / 2;
state.pitchers().iter().fold(0, |acc, pitcher| acc + if pitcher % target == 0 { 10 } else { 0 } - (target - pitcher).abs())
// -(state.pitchers().iter().map(|pitcher| (target - pitcher).abs()).min().unwrap())
}
// ビーム・サーチ。
pub fn answer(game: &Game, beam_width: i32) -> Option<Vec<Action>> {
// ノード。評価結果を入れるscoreを追加しました。
struct Node {
state: State,
answer: Vec<Action>,
score: i32
}
// BinaryHeap(priority queueが必要な場合はこれを使えとRustのドキュメントに書いてあった)で使えるように、PartialEqとEq、PartialOrd、Ordを実装します。
impl PartialEq for Node {
fn eq(&self, other: &Self) -> bool {
self.score == other.score
}
}
impl Eq for Node {}
impl PartialOrd for Node {
fn partial_cmp(&self, other: &Self) -> Option<Ordering> {
Some(self.cmp(&other))
}
}
impl Ord for Node {
fn cmp(&self, other: &Self) -> Ordering {
self.score.cmp(&other.score)
}
}
// 優先度付きキューと探索済みの集合を管理するためのセットを作成します。
let mut queue = BinaryHeap::new();
let mut visited = HashSet::new();
// キューに初期状態を追加します。
queue.push(Node {
state: game.initial_state(),
answer: Vec::new(),
score: 0
});
// 初期状態を探索済みにしておきます。
visited.insert(game.initial_state());
// キューが空でなければ、処理を繰り返します。
while !queue.is_empty() {
// 「次の」優先度付きキュー。
let mut next_queue = BinaryHeap::new();
// ビーム幅まで……
for _ in 0..min(beam_width, queue.len() as i32) {
// 次のノードを取得します。
let node = queue.pop().unwrap();
// 合法手すべてでて……
for action in game.legal_actions(&node.state) {
// 次の状態を取得します。
let next_state = game.next_state(&node.state, &action);
// 次の状態が探索済みでなければ……
if visited.insert(next_state.clone()) {
// 次の解答を取得します。
let next_answer = next_answer(&node.answer, &action);
// ゴールなら、その解答をリターンして終了します。
if game.is_goal(&next_state) {
return Some(next_answer);
}
// 次のスコアを取得します。
let next_score = score(&game, &next_state, &next_answer);
// 新しいノードを「次の」キューに追加します。
next_queue.push(Node {
state: next_state,
answer: next_answer,
score: next_score
});
}
}
}
// 「次の」キューを今のキューに設定します。
queue = next_queue;
}
// 正解が見つからない場合は、Noneを返します。
None
}
次の階層用のnext_queueを用意して、次の階層のノードをpushする先をnext_queueにして、あと、queueからpopする回数をbeam_widthまでにしただけ。それ以外は、最良優先探索のコードと同じなのでとってもかんたん。
で、これを実行してみる……にはbeam_widthの値を決めなければならないのですけど、今回の問題は単純すぎて、調べてみたところ、階層単位での状態数は最大でも3しかありませんでした。なので、beam_widthを2にして呼び出してみます。
(0, 2), [5, 0, 3]
(2, 1), [5, 3, 0]
(0, 2), [2, 3, 3]
(2, 1), [2, 5, 1]
(1, 0), [7, 0, 1]
(2, 1), [7, 1, 0]
(0, 2), [4, 1, 3]
はい、元ネタと同じ解答が出ました。最適解へ辿り着くためのノードがビームから漏れたという理由で、最適解が出なかったわけですな(最短手数の次の階層まで探索しているので、最適解は綺麗サッパリ捨てられちゃってます)。前述したように今回の問題は単純なので探索木の階層単位での状態数は最大でも3しかありませんから、ビーム幅を3にすると枝狩りされなくなって、どんなへっぽこな評価関数でも最適解が出ちゃいます。あと、評価関数を少し変えるだけでも、beam_widthが2でも最適解がでます。まぁ、元ネタの人もおっしゃっているように今回の問題は単純すぎて幅優先探索で十分なだけで、現実の複雑な問題では、ビーム・サーチはとても良いモノですよ。
まとめ
- 間違いを見つけたら、遠慮なくツッコミお願いします。
- ルール → 幅優先探索 → 最良優先探索 → ビーム・サーチの順で作ったら、とても楽でした。
- Rust良いよRust。このコード、C++と変わらない速度で動くんですよ!