More than 1 year has passed since last update.

BrainPad Advent CalendarAdvent Calendar 2021

3-SAT問題の量子ウォークによる探索～NumPyで実装してみた～

Last updated at 2021-12-24Posted at 2021-12-23

はじめに

今回は、量子ウォークの探索問題への応用について解説します。最初に量子ウォークの導入も兼ねて1次元の量子ウォークを解説します。続いて、3次元格子上の量子ウォークを定義します。その際、3次元格子上の条件式を命題論理と読み替えることで、条件式を満たす格子点の量子ウォークによる探索が、充足可能性問題（SAT）の解を探索することに等しいことを解説します。数式による解説だけでなく、NumPy による量子ウォークの実装とその計算結果も記載しました。

本記事の執筆に当たって、中山茂氏による書籍「量子アルゴリズム」¹ を参考にさせていただきました。3-SAT問題への適用もこの書籍で紹介されているテーマです。書籍においてブラ-ケット記法を使って説明されている量子ウォークの計算過程をすべて NumPy で再現するため、本記事では状態ベクトルや演算子をすべて行列で表現する工夫をしました。

量子ウォークについては、他にも多数の書籍が出版されています。特に、今野紀雄氏は、様々な応用を研究されていて書籍 ² もたくさん出版されているので、興味のある方はそちらも参考にしてください。

1次元の量子ウォーク

まずはじめに、量子ウォークの概念を理解するための導入として、1次元の量子ウォークを説明します。量子ウォークとは簡単にいうと、ランダムウォークを量子系へ拡張したものです。ランダムウォークでは等しい確率（コイン投げ）で右、または左に酔歩しますが、各ステップでは右か左のどちらかの向きしか選択できません。これに対して、量子ウォークでは、裏と表が重ね合わさった状態にあるコイン（量子コイン）により、右と左の両方を同時に選ぶことができます。この性質の違いが、以下で見るように確率分布に違いとして現れます。

1次元量子ウォーカーの状態ベクトル

ここでは、量子ウォークを $N$ ステップ進んだときのウォーカーの位置の確率振幅を求めます。最初に、初期状態を量子ウォーカーの位置状態と向きの状態（右か左）のテンソル積として定義します。具体的には、状態ベクトルを $2\times(2N+1)$ の行列と見なして、行列の1行目を右向き状態、2行目を左向き状態、行列の $n＋N$ 列目を一次元座標の位置 $n$ $(n=-N,\dots,-1,0,1,\dots,N)$ に対応づけます。このとき、量子ウォーカーの状態ベクトルと行列表現との対応は以下のようになります。

|n, R\rangle\quad \rightarrow \quad
\left[{\Psi_R \atop \Psi_L}\right] = 
\left[{0 \atop 0}{\dots \atop \dots}{1 \atop 0}{\dots \atop \dots}{0 \atop 0}\right]
{\leftarrow R \atop \leftarrow L}\\
\hspace{36 mm}\uparrow\\
\hspace{36 mm}n

量子コインの定義

量子コインは、量子ウォーカーの向きの状態（右向き、左向き）を変化させるユニタリ―変換として定義されます。古典コインとの違いとして、量子コインでは右向きと左向きを重ね合わせた状態を作り出すことができます。ここでは、量子コインを、アダマール変換として定義します。

|n, R\rangle \xrightarrow{C} {1 \over \sqrt{2}}\left(|n,R\rangle +|n, L\rangle\right), \quad
|n, L\rangle \xrightarrow{C} {1 \over \sqrt{2}}\left(|n,R\rangle -|n, L\rangle\right), \quad

ここで、記号 $C$ は、量子コインに対応するユニタリ―変換を表します。状態ベクトルの行列表現では、量子コイン $C$ は、以下の $2 \times 2$ 行列 $C$ により定義できます。

C = {1 \over \sqrt{2}}\left[{1 \atop 1}\quad{1 \atop -1}\right], \quad
\left[{\Psi_R \atop \Psi_L}\right] \rightarrow C \left[{\Psi_R \atop \Psi_L}\right]

1次元量子ウォーカーの移動

量子ウォーカーが右向き状態にあるときには右に1ステップ移動、左向き状態にあるときには左に1ステップ移動します。状態ベクトルで書くと、以下のようになります。

|n, R \rangle \xrightarrow{S} |n+1, R\rangle, \quad 
|n, L \rangle \xrightarrow{S} |n-1, L\rangle

ここで、記号 $S$ は、この移動に対応するユニタリ―変換を表します。右向きを正とするので左に1ステップ移動することは座標 $n$ を1減らすことになります。状態ベクトルの行列表現では、シフト演算子 $S$ は、上下の各行をそれぞれ右左に1ステップだけシフトする行列で定義できます。

S_R=\left[
\begin{array}{cc}
0 & 1 & 0 & \cdots & 0 & 0 & 0 \\
0 & 0 & 1 & \cdots & 0 & 0 & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\
0 & 0 & 0 & \cdots & 0 & 1 & 0 \\
0 & 0 & 0 & \cdots & 0 & 0 & 1 \\
1 & 0 & 0 & \cdots & 0 & 0 & 0 \\
\end{array}
\right], \quad
S_L=\left[
\begin{array}{cc}
0 & 0 & 0 & \cdots & 0 & 0 & 1 \\
1 & 0 & 0 & \cdots & 0 & 0 & 0 \\
0 & 1 & 0 & \cdots & 0 & 0 & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\
0 & 0 & 0 & \cdots & 1 & 0 & 0 \\
0 & 0 & 0 & \cdots & 0 & 1 & 0 \\
\end{array}
\right]

シフト変換を状態ベクトルの行列表現で表すと、以下のように行列の掛け算で定義できます。

\Psi_R \rightarrow \Psi_R S_R, \quad 
\Psi_L \rightarrow \Psi_L S_L

1次元量子ウォークのNumPyによる実装

以上見てきたように、1次元量子ウォークは状態ベクトル、演算子ともに行列で定義できます。本節では、量子ウォークの行列演算をNumPyを使って実装します。

import numpy as np

N = 20
Psi0 = np.zeros((2*N+1)*2).reshape((2,2*N+1)).astype(np.int)
Psi0[0, N] = 1

C = np.array([[1,1],[1,-1]])

SR = np.zeros((2*N+1)**2).reshape((2*N+1,2*N+1)).astype(np.int)
for i in range(2*N+1):
    SR[i,(i+1) % (2*N+1)] = 1

SL = np.zeros((2*N+1)**2).reshape((2*N+1,2*N+1)).astype(np.int)
for i in range(2*N+1):
    SL[i,(i-1) % (2*N+1)] = 1

量子ウォークの実施

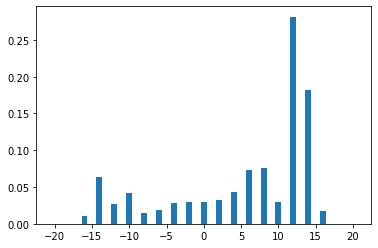
それでは、量子ウォークを実験してみましょう。20ステップ進んだ時の量子ウォーカーの位置の分布を求めます。初期状態として、右向き状態で座標原点 0 にいる状態 $|0, R\rangle$ からスタートすると20ステップ後の確率分布は右に偏った分布となります。

import numpy as np
import matplotlib.pyplot as plt

N = 20
Psi = Psi0
for n in range(N):
    tmp = np.dot(C,Psi)
    Psi = np.stack([np.dot(tmp[0,:],SR),
                    np.dot(tmp[1,:],SL)]).reshape(2,2*N+1)

prob = np.sum(np.square(Psi), axis=0)/2**N
print('確率分布の累積和:{:.1f}'.format(np.sum(prob)))

left = np.arange(2*N+1)-N
height = prob
plt.bar(left, height)

上記のように位置の分布が右に偏ってしまったのは、初期状態が右向き状態だったからです。量子ウォークの場合、次式のように初期状態を右向き状態と左向き状態の重ね合わせとして用意することができます。

{1 \over \sqrt{2}}\left(
|0,R\rangle + j|0,L\rangle
\right), \quad j \equiv \sqrt{-1}

NumPyだと以下のように書けます。

Psi0 = np.zeros((2*N+1)*2).reshape((2,2*N+1)).astype(np.complex)
Psi0[0, N] = 1/np.sqrt(2)
Psi0[1, N] = 1j/np.sqrt(2)

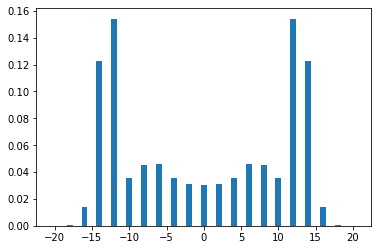
この初期状態からスタートして量子ウォークを20ステップ実施した場合の分布が下の図です。分布が原点を中心に左右対称になっていることが分かります。

量子ウォークの位置分布は、古典的なランダムウォークとは著しく異なります。ランダムウォークの場合、試行回数を増やしていくと位置分布は原点を中心とする正規分布に近づいていきます。それに対して、量子ウォークの位置分布はピークが原点から離れた両端付近にあります。実際、ステップ数 $N$ に対する平均移動距離の振る舞いで比較すると、ランダムウォークが $O(\sqrt{N})$ であるのに対して、量子ウォークは $O(N)$ であり、探索範囲が広く効率が良いことが分かります。

3次元格子上の量子ウォーク

つぎに、3次元格子上の量子ウォークについて解説します。3次元格子とは、立方体の8個の頂点（格子点）と12本の辺からなる有限な探索空間です。量子ウォーカーは、この有限な探索空間の上を動きながら、ある条件を満たす格子点を探索します。ある条件とは、格子点を2進数で付番したときに、その番号に対する条件式として定義されます。後で見るように、2進数の3桁を3つ論理値、条件式を命題論理式と読み替えることで、量子ウォークによる探索は、充足可能性問題の解法となります。

3次元格子点と3-SAT問題との対応

3-SAT問題とは、充足可能性問題（satisfiability problem, SAT）の一つです。充足可能性問題とは、Wikipediaによれば、「一つの命題論理式が与えられたとき、それに含まれる変数の値を偽 (False) あるいは真 (True) にうまく定めることによって全体の値を'真'にできるか、という問題」のことです。例えば、True か False の何れかの値を持つ変数 $x_1, x_2$ の関数 $f(x_1,x_2)$ を次式で定義します。

f(x_1,x_2)=(x_1 \vee x_2) \wedge (x_1 \vee \neg x_2) \wedge (\neg x_1 \vee \neg x_2)

ここで、$\neg$ は論理否定、$\vee$ は論理和、$\wedge$ は論理積を表します。このとき、関数 $f$ に関する充足可能性問題は、「$f(x_1, x_2) = {\small\tt True}$ となる $x_1$ と $x_2$ の組合せが存在するか？」という問題になります。上記の $f$ については、$(x_1, x_2) = ({\small\tt True}, {\small\tt False})$ の場合に $f$ は $\small\tt True$ となるので答えは 'Yes' となります。もちろん、関数（あるいは命題論理式）$f$ の定義によっては、$x_1$ と $x_2$ の如何なる組合せについても $f$ が $\small\tt False$ であり、答えが 'No' となる場合もあります。

関数 $f$ が表す命題論理式において括弧 $(,)$ で囲われた部分を節、節に含まれる変数をリテラルといいます。命題論理式において節が高々3つのリテラルを含むSATは、3-SATと呼ばれます。3-SATはNP完全な組合せ最適化問題であることが知られています。ここでは、書籍「量子アルゴリズム」で紹介されている3-SAT問題の3次元格子上の量子ウォークによる探索を、行列演算で定式化してNumPyで実装することを試みます。ただし、問題を簡単化するため3-SAT問題で使用できるリテラル変数を3変数に限定しています。

それでは、量子ウォークの探索空間である3次元格子がリテラル集合として解釈できることを説明します。3次元格子は立方体の8個の頂点（格子点）と12本の辺で構成され、8個の頂点は $0$ から $7$ までの整数で付番されています。量子ウォーカーは、これら8個の格子点を量子コインを振りながら辺に沿って移動します。このとき、量子ウォーカーの位置状態は格子点の番号で特定できるので、対応する状態ベクトルは、格子点の番号 $x$ により以下のように表すことができます。

|x\rangle \equiv |x_2 x_1 x_0 \rangle \quad x=0,1,\dots,7

ここで $x_2 x_1 x_0$ は、インデックス $x$ の2進数表記を表します。例えば、$x=3$ は2進数表記では $011$ なので $(x_2,x_1,x_0)=(0,1,1)$ となります。そこで、この2進数表記の3つの桁 $(x_2, x_1, x_0)$ を論理値と読み替えることで3-SATの3つのリテラルと解釈できます。例えば、$(x_2,x_1,x_0)=(0,1,1)$ は、リテラルとしては $({\small \tt False},{\small\tt True},{\small\tt True})$ となります。この読み替えにより、3次元格子において条件式 $f(x)=1$ を満たす解を量子ウォークで探索する問題は、$x$ の2進数表記をリテラルとする命題論理式 $f(x)$ で定義される3-SAT問題として解釈できます。

3-SAT命題論理式の定義関数の実装

関数 $f(x)$ の命題論理式としての実装を説明します。以下の手順で行います。

命題論理式を $\neg$, $\vee$, $\wedge$ を使って定義する。
$x$ を2進数表記 $(x_2, x_1, x_0)$ に変換する。
2進数の各桁の数値 0 または 1 を論理値 False または True に変換する。
命題論理式に手順3の論理値を代入して得られた結果を整数値に変換して出力する。

以下に、関数 $f(x)= x_2 \wedge \neg x_1 \wedge \neg x_0$ のNumPyによる実装例を示します。

def f(x):
    b = np.array([x % 2, (x % 4) // 2, x //4])
    b = b.astype(np.bool)
    #y = (b[0] & b[1] & b[2])|(~b[0] & ~b[1] & ~b[2])
    y = (b[0] & ~b[1] & ~b[2])
    return y.astype(np.int)

量子ウォークによる探索アルゴリズム

ここでは、量子ウォークによる3次元格子の探索アルゴリズムについて説明します。基本となるのは、Groverの探索アルゴリズムです。このアルゴリズムでは、条件式 $f(x)=1$ を満たす探索点については確率振幅を反転させ、それ以外の探索点については確率振幅をそれらの平均値の周りで反転させる演算（拡散）$D=2 |\Psi\rangle \langle \Psi|-{\mathbb I}$ を行います。こうすることで、$f(x)=1$ を満たす確率振幅がもっとも大きく増幅されるので、探索後の確率分布のピークを拾うことで条件式を満たす探索点を見つけることができるというアルゴリズムです。探索空間の規模 $N$ に対して、解を見つけるのに必要なステップ数は、古典的なランダムサーチが $O(N)$ であるのに対して、Groverのアルゴリズムでは $O(\sqrt{N})$ になることが知られています。

量子ウォークによる探索アルゴリズムにおいても、条件式 $f(x)=1$ を満たす格子点における反転演算子 $I_f$、それ以外の格子点における拡散演算子 $D_f$ を定義さえすれば、Groverのアルゴリズムと同様に探索後の確率分布のピークを拾うことで、条件式を満たす格子点を見つけることができます。

3次元格子上の状態ベクトル

3次元格子上の状態ベクトル（あるいは確率振幅）は、量子ウォーカーの位置（格子点）を表す8次元状態ベクトル $|x \rangle$ $(x=0,\dots,7)$ と移動方向（格子点で交わる辺）を表す3次元状態ベクトル $|i\rangle$ $(i=0,1,2)$ のテンソル積 $|x\rangle \otimes |i\rangle$ として定義されます。これらのテンソル積で表される基底ベクトルは、24次元の one-hot ベクトルとして表すことができます。

|x=1\rangle \otimes |i=0\rangle \quad \leftrightarrow \quad
\left[
\begin{array}{cl}
0 & \\
1 & \leftarrow x=1 \\
\vdots & \leftarrow i=0 \\
0 & \\
- & \\
0 & \\
\vdots & \leftarrow i=1 \\
0 & \\
- & \\
0 & \\
\vdots & \leftarrow i=2 \\
0 &
\end{array}
\hspace{-23 mm}\right]

したがって、これら基底ベクトルの均等な重ね合わせ状態 $|\Psi_0\rangle$ は、以下のようにすべての成分が1である24次元ベクトルとして表されます。

|\Psi_0 \rangle = {1 \over \sqrt{24}}\sum_{x=0}^7 \sum_{i=0}^2 |x\rangle \otimes |i\rangle
\quad \leftrightarrow \quad
\Psi_0 = {1 \over \sqrt{24}}\left[
\begin{array}{c}
1 \\
\vdots \\
1 \\
- \\
1 \\
\vdots \\
1 \\
- \\
1 \\
\vdots \\
1
\end{array}
\right]

3次元格子上の量子コイン

量子ウォークによる探索を実現するには、Groverの探索アルゴリズムにおける反転演算子と拡散演算子に相当するものを3次元格子について定義する必要があります。反転演算子は、条件式 $f(x)=1$ を満たす格子点のみ状態ベクトルに $-1$ を掛ける演算子として定義されます。一方、拡散演算子は、条件式を満たさない格子点だけに作用します。これらの演算子を実現するには、条件式を満たす格子点のみ抽出する射影演算子 ${\bf P}_f$ が必要です。これは $1-f(x)$ を成分とする $8\times8$ 対角行列として定義できます。

{\bf P}_f = {\rm diag} \left\{1-f(x); x=0, \dots,7\right\}

実際、${\bf P}_f$ を状態ベクトルに作用した場合、条件式 $f(x)=1$ を満たす格子点の状態ベクトルは $0$ となり、条件式を満たさない状態ベクトルはそのままであることが分かります。ゆえに、反転演算子 ${\bf I}_f$ は射影演算子を用いて次式のように定義できます。

{\bf I}_f = {\bf P}_f - {\mathbb I}_8 = {\rm diag} \left\{-f(x); x=0, \dots,7\right\}

一方、拡散演算子 ${\bf D}$ は、移動方向の3次元状態ベクトルについて均等な状態ベクトル $|\psi\rangle = {1 \over \sqrt{3}}[1,1,1]^t$ を用いて、次式のように定義できます。

{\bf D} = 2|\psi\rangle \langle \psi|-{\mathbb I}_3 
= {1 \over 3}\left[
\begin{array}{ccc}
-1 & 2 & 2 \\
2 & -1 & 2 \\
2 & 2 & -1
\end{array}
\right]

以上より、位置状態ベクトルと向き状態ベクトルのテンソル積に作用する演算子として、反転演算子 $I_f$ および拡散演算子 $D_f$ を次式のように定義できます。

I_f = {\bf I}_f \otimes {\mathbb I}_3
= \left[
\begin{array}{ccc}
{\bf I}_f &  &  \\
 & {\bf I}_f &  \\
 &  & {\bf I}_f
\end{array}
\right], \quad
D_f = {\bf P}_f \otimes {\bf D}
= {1 \over 3} \left[
\begin{array}{ccc}
-{\bf P}_f & 2{\bf P}_f & 2{\bf P}_f \\
2{\bf P}_f & -{\bf P}_f & 2{\bf P}_f \\
2{\bf P}_f & 2{\bf P}_f & -{\bf P}_f
\end{array}
\right]

上式の反転演算子 $I_f$ と拡散演算子 $D_f$ は格子点について互いに排他的なので、これらを足した演算子を量子コイン $C_f$ と定義することができます。

C_f = I_f + D_f = {1 \over 3} \left[
\begin{array}{ccc}
2{\bf P}_f - 3\,{\mathbb I}_8 & 2{\bf P}_f & 2{\bf P}_f \\
2{\bf P}_f & 2{\bf P}_f - 3\,{\mathbb I}_8 & 2{\bf P}_f \\
2{\bf P}_f & 2{\bf P}_f & 2{\bf P}_f - 3\,{\mathbb I}_8
\end{array}
\right]

量子コインのNumPyによる実装は以下の通りです。

import numpy as np

P = np.diag([1-f(x) for x in range(8)])
I = np.diag(np.ones(8)).astype(np.int)
zero8 = np.zeros(64).reshape(8,8).astype(np.int)

C = np.vstack(
[
    np.hstack((2*P-3*I, 2*P, 2*P)),
    np.hstack((2*P, 2*P-3*I, 2*P)),
    np.hstack((2*P, 2*P, 2*P-3*I))
]
)

3次元格子点上のシフト演算子

向き状態の基底ベクトル $|0\rangle$, $|1\rangle$, $|2\rangle$ は、それぞれ格子点の2進数1桁目、2桁目、3桁目を反転する方向を示しています。これに対応して、3次元格子上のシフト演算子 ${\bf S}_0$, ${\bf S}_1$, ${\bf S}_2$ は、それぞれ格子点の2進数1桁目、2桁目、3桁目を反転する演算子として定義できます。行列表現は、以下のように書けます。

{\bf S}_0 = \left[
\begin{array}{cccc}
{\bf X} & {\mathbb O}_2 & {\mathbb O}_2 & {\mathbb O}_2 \\
{\mathbb O}_2 & {\bf X} & {\mathbb O}_2 & {\mathbb O}_2 \\
{\mathbb O}_2 & {\mathbb O}_2 & {\bf X} & {\mathbb O}_2 \\
{\mathbb O}_2 & {\mathbb O}_2 & {\mathbb O}_2 & {\bf X}
\end{array}
\right], \quad
{\bf S}_1 = \left[
\begin{array}{cccc}
{\mathbb O}_2 & {\mathbb I}_2 & {\mathbb O}_2 & {\mathbb O}_2 \\
{\mathbb I}_2 & {\mathbb O}_2 & {\mathbb O}_2 & {\mathbb O}_2 \\
{\mathbb O}_2 & {\mathbb O}_2 & {\mathbb O}_2 & {\mathbb I}_2 \\
{\mathbb O}_2 & {\mathbb O}_2 & {\mathbb I}_2 & {\mathbb O}_2
\end{array}
\right], \quad
{\bf S}_2 = \left[
\begin{array}{cccc}
{\mathbb O}_2 & {\mathbb O}_2 & {\mathbb I}_2 & {\mathbb O}_2 \\
{\mathbb O}_2 & {\mathbb O}_2 & {\mathbb O}_2 & {\mathbb I}_2 \\
{\mathbb I}_2 & {\mathbb O}_2 & {\mathbb O}_2 & {\mathbb O}_2 \\
{\mathbb O}_2 & {\mathbb I}_2 & {\mathbb O}_2 & {\mathbb O}_2
\end{array}
\right]

上式において $2 \times 2$ 行列 ${\bf X}$, ${\mathbb O}_2$, ${\mathbb I}_2$ を以下のように定義しました。

{\bf X}=\left[
\begin{array}{cc}
0 & 1 \\
1 & 0 
\end{array}
\right], \quad
{\mathbb O}_2=\left[
\begin{array}{cc}
0 & 0 \\
0 & 0 
\end{array}
\right], \quad
{\mathbb I}_2=\left[
\begin{array}{cc}
1 & 0 \\
0 & 1 
\end{array}
\right]

定義式から、${\bf S}_0$ が格子点のシフト $0 \leftrightarrow 1$, $2 \leftrightarrow 3$, $4 \leftrightarrow 5$, $6 \leftrightarrow 7$ を誘導することが分かります。さらに、${\bf S}_1$ は $[0,1] \leftrightarrow [2,3]$, $[4,5] \leftrightarrow [6,7]$、${\bf S}_2$ は $[0,1,2,3] \leftrightarrow [4,5,6,7]$ を誘導することも明らかです。

これら3つのシフト演算子をブロック対角にまとめることで、3次元格子上のシフト演算子 $S$ を定義します。

S=\left[
\begin{array}{ccc}
{\bf S}_0 & {\mathbb O}_8 & {\mathbb O}_8 \\
{\mathbb O}_8 & {\bf S}_1 & {\mathbb O}_8\\
{\mathbb O}_8 & {\mathbb O}_8 & {\bf S}_2
\end{array}
\right]

シフト演算子のNumPyによる実装は以下の通りです。

import numpy as np

sigma1 = np.array([[0,1],[1,0]])
sigma0 = np.array([[1,0],[0,1]])
zero = np.array([[0,0],[0,0]])

S0 = np.vstack(
[
    np.hstack([sigma1, zero, zero, zero]),
    np.hstack([zero, sigma1, zero, zero]),
    np.hstack([zero, zero, sigma1, zero]),
    np.hstack([zero, zero, zero, sigma1])
]
)

S1 = np.vstack(
[
    np.hstack([zero, sigma0, zero, zero]),
    np.hstack([sigma0, zero, zero, zero]),
    np.hstack([zero, zero, zero, sigma0]),
    np.hstack([zero, zero, sigma0, zero])
]
)

S2 = np.vstack(
[
    np.hstack([zero, zero, sigma0, zero]),
    np.hstack([zero, zero, zero, sigma0]),
    np.hstack([sigma0, zero, zero, zero]),
    np.hstack([zero, sigma0, zero, zero])
]
)

S = np.vstack(
[
    np.hstack([S0, zero8, zero8]),
    np.hstack([zero8, S1, zero8]),
    np.hstack([zero8, zero8, S2])
]
)

量子ウォークによる3次元格子の探索

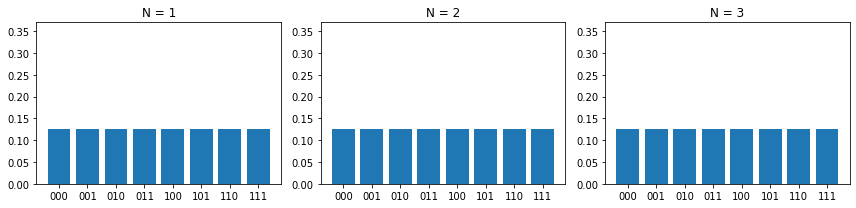
これまでに定義した量子コインとシフト演算子を用いて、3次元格子上の量子ウォークによる探索を実施します。初期状態として、基底ベクトルの均等な重ね合わせ状態 $\Psi_0$ からスタートします。探索のステップ数 $N=3$ として各ステップにおける格子上の確率分布を見比べてみます。

import numpy as np
import matplotlib.pyplot as plt

SC = np.dot(S, C)

N = 3
prob = []
Psi = Psi0
for n in range(N):
    Psi = np.dot(SC, Psi)/3
    tmp = Psi.reshape(3, 8)
    prob.append(np.sum(np.square(tmp), axis=0)/24)

left = ['000','001','010','011','100','101','110','111']

fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(12, 3),
                         tight_layout=True)
for n in range(N):
    height = prob[n]
    axes[n].bar(left, height)
    axes[n].set_title('N = ' + str(n+1))
    axes[n].set_ylim(0,0.37)

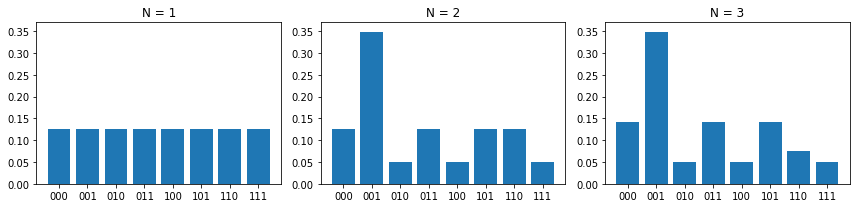
グラフから分かる通り、$N=1$ では確率分布は格子点によらず一様です。$N=2$ において、条件式を満たす $x=001$ において確率分布にピークが見られます。$N=3$ では、確率分布において $N=2$ から大きな変化はなく、2ステップの探索で解が見つかりました。

他の3-SAT問題への適用

量子ウォークの有効性を見るために、ここでは、幾つかの3-SAT問題に量子ウォークを適用してみます。3-SAT問題は命題論理式を記述する関数 $f(x)$ によって決まります。関数 $f(x)$ の定義式を変更すると、それに伴い位置状態の射影演算子が変更を受けるので、量子コインの再定義が必要になります。Pythonコードを書きかえる際は、以下のように $f(x)$ と ${\bf P}_f$ および $C_f$ を再定義した上で量子ウォークによる探索を実行します。

def f(x):
    b = np.array([x % 2, (x % 4) // 2, x //4])
    b = b.astype(np.bool)
    y = (b[1] | b[2]) & (b[1] | ~b[2]) & (~b[1] | ~b[2])
    #y = (b[1] | b[2]) & (~b[1] | b[2]) & (b[1] | ~b[2]) & (~b[1] | ~b[2])
    #y = (b[0] & b[1] & b[2])|(~b[0] & ~b[1] & ~b[2])
    #y = (b[0] & ~b[1] & ~b[2])
    return y.astype(np.int)

P = np.diag([1-f(x) for x in range(8)])
C = np.vstack(
[
    np.hstack((2*P-3*I, 2*P, 2*P)),
    np.hstack((2*P, 2*P-3*I, 2*P)),
    np.hstack((2*P, 2*P, 2*P-3*I))
]
)

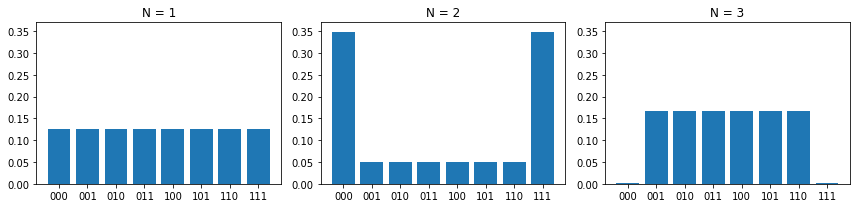
3-SAT問題として以下の3つを試します。

$(x_1 \vee x_2) \wedge (x_1 \vee \neg x_2) \wedge (\neg x_1 \vee \neg x_2)$
$(x_1 \vee x_2) \wedge (\neg x_1 \vee x_2) \wedge (x_1 \vee \neg x_2) \wedge (\neg x_1 \vee \neg x_2)$
$(x_0 \wedge x_1 \wedge x_2) \vee (\neg x_0 \wedge \neg x_1 \wedge \neg x_2)$

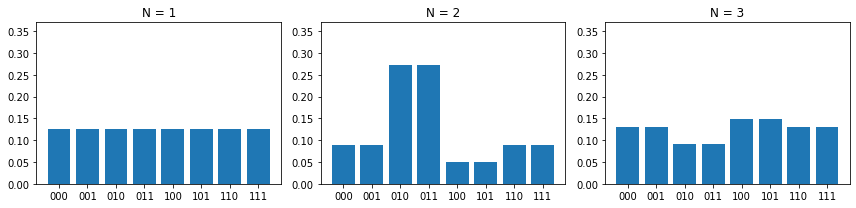
最初の命題は、$x_1=\small \tt True$、$x_2=\small \tt False$ のとき $\small \tt True$ なので、$010$ または $011$ においてピークが確認できます。

2番目の命題は、$x_1$ と $x_2$ のすべての組合せについて $\small \tt False$ なので確率分布は一様でピークは現れません。

最後の命題は、書籍「量子アルゴリズム」でも取り上げられているもので、すべてのリテラルが $\small \tt True$ または $\small \tt False$ のとき $\small \tt True$ となります。したがって、$000$ と $111$ に2つのピークが現れます。

まとめ

今回は、量子ウォークをテーマとして取り上げました。量子ウォークの応用例は他にも多数あります。例えば、検索エンジンのページランクアルゴリズムの改良 ³ などの試みは、身近な機械学習アルゴリズムへの応用例として興味深いです。さらに、IBM Q や Amazon Braket など量子コンピュータの実機を使った実験をおこなうのも一興かと思います。量子ウォークの原論文 ⁴ については、本記事で紹介した書籍の参考文献を参照してください。

中山茂著「量子アルゴリズム]」2014年技報堂出版（本書は、量子アルゴリズムの詳細な解説がなされており、私は多くを学ばせていただきました。ただし、3.1節における密度行列の運動方程式の解釈に誤りがあります。密度行列の時間発展はハイゼンベルグ描像ではなくシュレディンガー描像です。） ↩
今野紀雄著「量子探索～量子ウォークが拓く最先端アルゴリズム～」2021年近代科学社（他にも多数の著書があります。） ↩
大関真之監訳「量子コンピュータによる機械学習」2020年共立出版 ↩
Ambainis, "Quantum walks and their algorithmic application" ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

3-SAT問題の量子ウォークによる探索 ～NumPyで実装してみた～