Quaternion：四元数と回転群のトポロジーについて

0. はじめに

最近、機械学習の界隈でも四元数（Quaternion）という言葉をよく耳にします。四元数は、端的に行ってしまえば3次元実空間の回転群の表現のひとつであり、電子スピンや量子ビット演算を記述するパウリ行列とも関係しています。ジャイロ制御や3Dコンピュータグラフィックスなど工学的な応用との関連で、Qiitaにおいても四元数に関する多くの解説記事¹が見つけられます。しかし、ジンバルロックの解消など回転群のトポロジーとの関連まで踏み込んだ解説は見受けられません²。本記事では、その辺の数学的な背景を踏まえて四元数によるジンバルロックの解消について解説します。

1. オイラー角による回転の表現

オイラー角とは、3次元空間における任意の回転を3軸の周りの回転で表現する試みであり、軸の取り方により幾つかの定義があります。ここでは、例として飛行機の姿勢制御を考えます。飛行機の胴体の軸を x 軸、翼が拡がる方向を y 軸、機体の上下を貫く方向を z 軸と定義し、x-y-z が左手系を成すように座標軸を定義します。このとき、機体を左右に振る回転（z 軸周り）をヨー（yaw）、機体を上下に振る回転（y 軸周り）をピッチ（pitch）、機体の胴体軸周りの回転（x 軸周り）をロール（roll）と呼びます（下図を参照）。

3次元の回転操作は、3行3列の行列によって表現できます。回転軸が x, y, z の3軸の何れかに一致する場合、3次元回転は残りの2軸がなす平面上での2次元回転に帰着します。ヨー、ピッチ、ロールの回転角が $\alpha, \beta, \gamma$ に対応する回転の行列表現 $\bf R$ は以下の様に3つの回転行列の積として記述できます。

{\bf R} = \left[
\begin{matrix}
1 & 0 & 0 \\
0 & \cos\alpha & -\sin\alpha \\
0 & \sin\alpha & \cos\alpha 
\end{matrix}\right]\left[
\begin{matrix}
\cos\beta & 0 & \sin\beta\\
0 & 1 & 0\\
-\sin\beta & 0 & \cos\beta
\end{matrix}\right]\left[
\begin{matrix}
\cos\gamma & -\sin\gamma & 0\\
\sin\gamma & \cos\gamma & 0\\
0 & 0 & 1
\end{matrix}\right]

2. ジンバルロック

次に、ジンバルロック³について考えてみましょう。ジンバルロック（Gimbal lock）とは、オイラー角の3軸に対応する3つの回転面のうち2つが一致してしまい、制御が効かなくなる問題です。例えば、ヨーを振った後にピッチを90度振って機首を鉛直上向きにすると、ロールの回転面がヨーの回転面と一致してしまいます（下図）。つまり機首の方向を変えようとしても機体が自転（ロール）してしまって制御不能に陥ってしまいます。このような状況のことをジンバルロックといいます（ヨーとロールの回転面（ジンバル）が一致してしまうので）。実際、人類を月に送ったアポロ計画でも、ジンバルロックを如何に回避するかに頭を悩ませたそうです³。

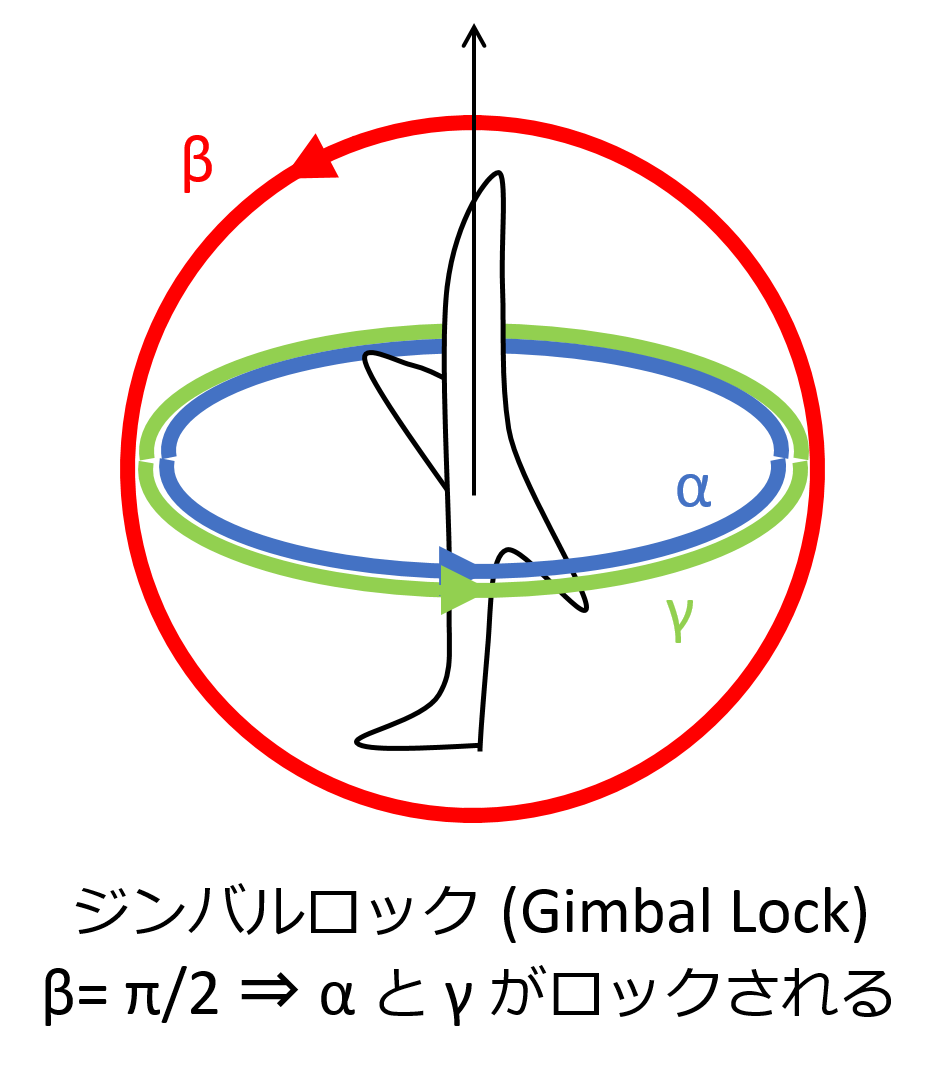
3. オイラー角による回転表現のトポロジー

ジンバルロックが生じる原因は、回転群の表現とオイラー角による表現との間でトポロジーが異なることにあります。そこで、オイラー角による回転表現のトポロジーを考察しましょう。

オイラー角のうちヨーとピッチを考えます。両変数ともに1次元の回転なので、その範囲は0~2$\pi$であり、0と2$\pi$は周期的境界条件により同一視されます。2つの回転角を平面であらわすと長方形のシートとなり上辺と下辺、右辺と左辺が向きも含めて一致しています。そこで向きが一致するようにシートの上辺と下辺を貼り合わせるとチューブ状になります。さらに、このチューブの両端を向きが一致するように貼り合わせるとドーナツ状の形になります。数学では、このような形をトーラスと呼びます。つまり、ヨーとピッチの成す多様体は、2次元トーラス $T^2$ であることがわ分かりました。

この2次元トーラス上の各点における法線ベクトルは、ロールの回転軸に対応しています。3次元回転をユニークに定義するには、トーラス上の異なる2点で法線ベクトルの向きが異なる必要がありますが、トーラス上のピッチが90度に対応する円周上では、法線ベクトルが全て同じ方向に揃ってしまいます。結果として、この円周上ではヨーの値を変えてもロール軸の向きを変えることはできません。こうしてジンバルロックが生じることになります。

4. 回転群の表現とトポロジー

オイラー角の表現空間では、回転軸の向きを決める多様体が2次元トーラス $T^2$ であり、その部分空間（ピッチ$\pm$90度の円周）上では法線ベクトルの方向が揃ってしまうことがジンバルロックの原因でした。ということは、回転軸を決める2次元多様体として、場所ごとに法線ベクトルの向きが異なる多様体を選べば、ジンバルロックは解消するはずです。そのような2次元多様体として最も簡単なものは2次元球面 $S^2$ です。

実際、3次元回転は、回転軸の向きを決める単位ベクトル $\vec{n}$ とその周りの回転角 $\psi$ によってユニークに記述できます。単位ベクトル $\vec{n}$ の終点は、2次元球面 $S^2$ 上に拘束されており、その向きは2次元極座標 $(\phi, \theta)$ により以下の様に表すことができます。

$$
\vec{n} = (\sin\theta\cos\phi,,\sin\theta\sin\phi,,\cos\theta)
$$

極座標系は、緯度と経度により球面上の点を記述する座標系であり、同心円群とそれらに直行する放射状の直線群とからなります。円形のシートを考えると、その中心が緯度0度（北極）、境界円周が緯度180度（南極）に対応しています。このシートの境界円周上の点は全て同一と見なされるので、円形シートの境界円周を縮めるように変形していくと、巾着袋が閉じるように2次元球面 $S^2$ へと変形されます。

5. Quaternion による回転群の表現

3次元回転のパラメータは、単位ベクトル $\vec{n}$ とその周りの回転角 $\psi$ でユニークに記述できることがわかりました。次に、これらのパラメータを使って回転操作（演算）を定義する必要があります。ここで四元数が登場します。

四元数（quaternion）は、単位元 $\bf 1$ と、積において互いに非可換な3つの虚数 $\bf i$, $\bf j$, $\bf k$ によって定義される代数です。以下のルールに従います。

{\bf i}^2 = {\bf j}^2 = {\bf k}^2 = -{\bf 1} \\
{\bf i j} = -{\bf j i} = {\bf k}, \quad
{\bf j k} = -{\bf k j} = {\bf i}, \quad
{\bf k i} = -{\bf i k} = {\bf j}

任意の回転操作 $Q(\vec{n};\psi)$ は、四元数を使って以下の様に定義できます。

Q(\vec{n};\psi) = {\bf 1} \cos\left({\psi \over 2}\right) 
- (\vec{n} \cdot \vec{q}) \sin\left({\psi \over 2}\right)

ここで、便宜上、quaternion ベクトル $\vec{q} = ({\bf i}, {\bf j}, {\bf k})$ を定義しました。

回転角が2で割られているのは、四元数による表現が、回転群の2価表現 $SU(2)$ に対応しているからです。複数の回転操作は、四元数 $Q \equiv Q(\vec{n}, \phi)$ の積演算で表されます。四元数は積演算について閉じているので、四元数の積もまた四元数であり一つの3次元回転に対応しています。

ちなみに、以下の変換式により、四元数による回転操作から対応する3次元空間の回転行列 ${\bf R}(\vec{n},\psi)$ を計算することもできます。

Q^\dagger(\vec{n},\psi)\,\vec{q}\,Q(\vec{n},\psi) = {\bf R}(\vec{n},\psi) \,\vec{q}

ここで $Q^\dagger(\vec{n},\psi)$ は、$Q$ の複素共役であり次式で定義されます。

Q^\dagger(\vec{n},\psi)= {\bf 1} \cos\left({\psi \over 2}\right) 
+ (\vec{n} \cdot \vec{q}) \sin\left({\psi \over 2}\right),\quad

計算の詳細は示しませんが、上記の変換式から以下の結果が得られます（$R_{ab}$ は回転行列 $\bf R$ の $a$ 行 $b$ 列成分を意味します）。

R_{ab}(\vec{n},\psi)= (\delta_{ab} - n_a n_b)\cos\psi 
- \epsilon_{abc} n_c \sin\psi + n_a n_b

ここで $\delta_{ab}$ はクロネッカーのデルタ記号、$\epsilon_{abc}$ は、3次元の完全反対称テンソル（レビチビタ記号）を意味します。

6. Quaternion によるジンバルロックの解消

ジンバルロックが quaternion により具体的に解消することを計算で確かめます。前節で説明したようにジンバルロックは、オイラー角でピッチを90度にしたときに生じます。ヨー、ピッチ、ロールの軸 x-y-z が左手系をなし、それらの回転角を $(\alpha, \beta, \gamma)$ と定義すると、対応する回転操作は3次元回転行列の積として計算されます（次式参照、$e_x$, $e_y$, $e_z$ は、それぞれ $x$, $y$, $z$ 方向の単位ベクトル）。

\begin{aligned}
{\bf R} &= {\bf R}(e_x,\alpha){\bf R}(e_y,\beta=\pi/2){\bf R}(e_z,\gamma)\\
&=\left[
\begin{matrix}
1 & 0 & 0 \\
0 & \cos\alpha & -\sin\alpha \\
0 & \sin\alpha & \cos\alpha 
\end{matrix}\right]\left[
\begin{matrix}
0 & 0 & 1\\
0 & 1 & 0\\
-1 & 0 & 0
\end{matrix}\right]\left[
\begin{matrix}
\cos\gamma & -\sin\gamma & 0\\
\sin\gamma & \cos\gamma & 0\\
0 & 0 & 1
\end{matrix}\right]\\
&=\left[
\begin{matrix}
0 & 0 & 1 \\
\sin(\alpha+\gamma) & \cos(\alpha+\gamma) & 0\\
-\cos(\alpha+\gamma) & \sin(\alpha+\gamma) & 0
\end{matrix}\right]
\end{aligned}

最後の行列は、x 軸と z 軸を交換した後、z 軸周りに $\alpha+\gamma$ 回転する操作を表しており、ヨーとロールの軸が区別できない状況を表しています。

同じ回転操作を、今度は quaternion で計算すると、計算の詳細は省略しますが以下の結果が得られます。

\begin{aligned}
Q &= Q(e_x,\alpha)Q(e_y,\beta=\pi/2)Q(e_z,\gamma) \\
&= \bigg[{\bf 1} \cos\left({\alpha \over 2}\right) 
+ {\bf i} \sin\left({\alpha \over 2}\right)\bigg]\left[
{\bf 1}{1 \over \sqrt 2} + {\bf j}{1 \over \sqrt 2}\right]\bigg[
{\bf 1} \cos\left({\gamma \over 2}\right) 
+ {\bf k} \sin\left({\gamma \over 2}\right)\bigg] \\
&= {1 \over \sqrt 2}\bigg[{\bf 1} \cos\left({\alpha+\gamma \over 2}\right)
+{\bf i} \sin\left({\alpha+\gamma \over 2}\right)
+{\bf j} \cos\left({\alpha+\gamma \over 2}\right)
+{\bf k} \sin\left({\alpha+\gamma \over 2}\right)\bigg]
\end{aligned}

こうして計算された $Q$ もまた quaternion ですから、対応する回転軸ベクトル $\vec{n}$ と回転角 $\chi$ を使って以下の様に記述することができるはずです。

Q = {\bf 1} \cos\left({\chi \over 2}\right) 
- (\vec{n} \cdot \vec{q}) \sin\left({\chi \over 2}\right) 

$Q$ の2つの表式が等しいことから、回転角 $\chi$ および回転軸 $\vec{n}=(n_1, n_2, n_3)$ は次式で表されることが分かります。

\cos\left({\chi\over 2}\right) = 
{1 \over \sqrt 2}\cos\left({\alpha+\gamma\over 2}\right), \quad
\sin\left({\chi\over 2}\right) = 
{1 \over \sqrt 2}\sqrt{ 1 + \sin^2 \left({\alpha+\gamma\over 2}\right)}\\
n_1 =\,n_3 = \frac{\sin\left({\alpha+\gamma\over 2}\right)}{\sqrt{ 1 + \sin^2 \left({\alpha+\gamma\over 2}\right)}}, \quad
n_2 =  \frac{\cos\left({\alpha+\gamma\over 2}\right)}{\sqrt{ 1 + \sin^2 \left({\alpha+\gamma\over 2}\right)}} 

この場合、回転軸 $\vec{n}$ は、z-y-z 軸の何れとも一致しない方向を向いており、回転角も $\alpha+\gamma$ とは一致しません。オイラー角による表現では、ヨーとロールの回転軸が一致してジンバルロックが生じてしまう状況でも、quaternion 表現では非自明な回転軸周りの回転として一意に定義できています。

実際、x-y-z の3軸に対応する四元数 $\bf i$, $\bf j$, $\bf k$ をそれぞれquaternion 演算子 $Q$ で回転させると以下の結果が得られます。

\begin{aligned}
Q^\dagger {\bf i}\, Q &= {\bf k} \\
Q^\dagger {\bf j}\, Q &= {\bf i} \sin(\alpha+\gamma) + {\bf  j}\cos(\alpha+\gamma)\\
Q^\dagger {\bf k} Q &= -{\bf i} \cos(\alpha+\gamma) + {\bf  j}\sin(\alpha+\gamma)
\end{aligned}

つまり単位ベクトル $\vec{n}$ 周りの角度 $\chi$ の回転により、x-y-z 軸が先に計算した回転行列 $\bf R$ による回転を再現していることが分かります。

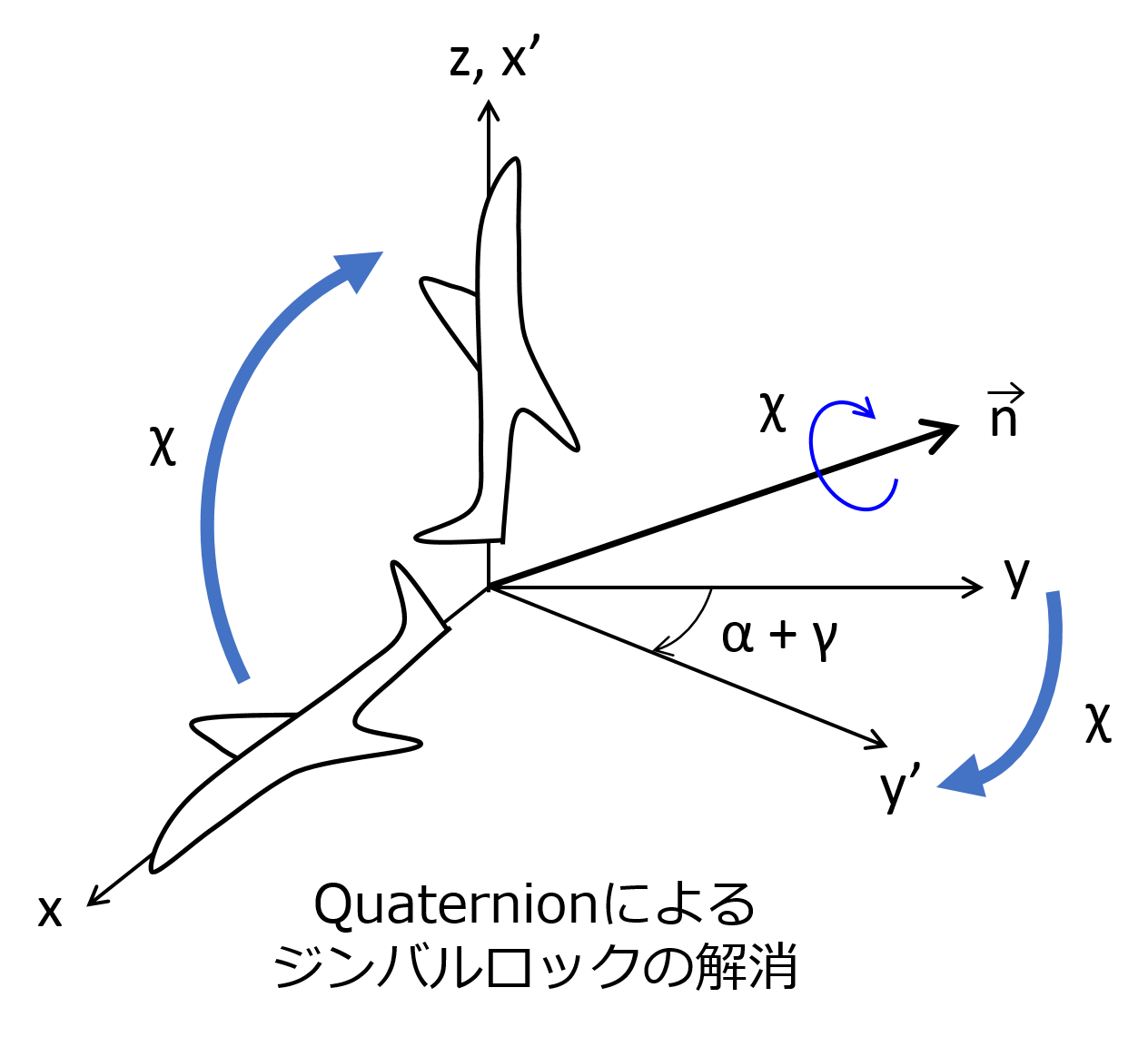
7. まとめ

今回は、いままで気になっていたジンバルロックと四元数との関係についてトポロジーの観点から考察を行いました。トポロジーの違いがジンバルロックという工学上の問題を引き起こすというのは大変に興味深いと思います。最近では、深層強化学習を使った機械制御なども研究されてきていますが、四元数は回転群のスムースな表現形式として活用されているようです。

付録：Quaternion とパウリ行列との関係

四元数の3つの虚数 $\bf i$, $\bf j$, $\bf k$ は積について非可換な代数にしたがいます。数の概念に非可換性を取り込んで拡張したものは Grassmann 数と呼ばれ数学や物理学で使われています。しかし、行列演算を用いれば非可換積を具体的にイメージすることができます。実際、四元数の基底は、$2\times2$ 単位行列とパウリ行列（Pauli matrices）により表現できます。

I =\left[\begin{matrix} 1 & 0 \\ 0 & 1\end{matrix}\right], \quad
\sigma_x = \left[\begin{matrix} 0 & 1 \\ 1 & 0\end{matrix}\right], \quad
\sigma_y = \left[\begin{matrix} 0 & -i \\ i & 0\end{matrix}\right], \quad
\sigma_z = \left[\begin{matrix} 1 & 0 \\ 0 & -1\end{matrix}\right].

四元数の単位元 $\bf 1$ を単位行列 $I$ として、3つの虚数基底 $\bf i$, $\bf j$, $\bf k$ は、それぞれパウリ行列と以下の様に関係づけられます。

{\bf i} = -i \sigma_x, \quad {\bf j} = -i \sigma_y, \quad {\bf k} = -i \sigma_z.

1. つい最近も詳しい解説記事が投稿されています。例えば https://qiita.com/drken/items/0639cf34cce14e8d58a5 ↩

2. ジンバルロックとの関連に触れた記事として以下があります。https://qiita.com/takaishi78/items/a0fc972188d1db057194 ↩

3. ジンバルロックについては、Wikipediaの英語版記事が分かりやすいです。本稿もこの解説をもとにしています。https://en.wikipedia.org/wiki/Gimbal_lock ↩ ↩²