今回は、応用数学からテーマを選びました。空間充填曲線の一つであるヒルベルト曲線とそれを用いた空間インデックスについて解説します。
はじめに
インターネットやスマートフォンの普及にともない、リアルタイムで位置情報をやり取りするサービスが増えてきました。これらサービスを支える技術として、位置時間情報を効率的に検索するための空間インデックスを生成する技術が不可欠です。空間インデックスには、kd木などに代表される木構造にもとづくインデックスの他に、空間充填曲線を利用したインデックスがあります。
空間充填曲線とはフラクタル図形の一種であり、一本の曲線により2次元平面(さらには3次元以上の高次元空間も)を埋め尽くすことができます。こうした曲線にそって空間上の任意の点に1次元の文字コードをインデックスとして付与することができます。こうした技術は、カーナビなどGPSによる位置・時間情報の通信などでも実際に使われています。また、ウェブ上のサービスとしては、Geohash1やGeocoding2が有名です。
以下では、空間充填曲線の一つであるヒルベルト曲線を紹介し、実際にそれを用いて緯度・経度の情報を16進数でコード化する方法を解説します3。
空間充填曲線について
ヒルベルト曲線とは?
通常、微分可能な(滑らかな)曲線は局所的には太さがない直線で近似できます。一次元(=太さゼロ)の直線をどれだけ並べても平面を埋めることはできません。しかし、自己相似図形のように同じパターンが再帰的に繰り返す構造(フラクタル構造)を持つ曲線の場合、局所的な構造が大域的な構造と同様の複雑さを保つため、いたるところ微分可能ではなく通常の曲線とは異なった性質を示します。実際、このような曲線を使えば平面を埋め尽くすことができ、平面状の任意の点に、一本の曲線に沿ってたどり着くことができます。
こうしたアイデアのもと、空間充填曲線の具体例が数学者ペアノにより提唱され、その後いろんな数学者がその実例を提唱しました。今回は、その中でも有名なヒルベルト曲線を紹介します。ヒルベルト曲線は、下図にあるようにコの字を向きを変えながら再帰的に繰り返すことで正方形領域を充填する曲線として定義されます。
まず最初に正方領域を考えます。この正方形を4分割しておいてコの字で4領域の重心点を結びます(図の左端)。次に正方形の各4領域をさらに4分割して同様に小さなコの字の描き、その向きを変えつつ大きなコの字に沿って移動しながら連結させていくと、正方形の16領域を1本の曲線でたどることができます(図の左から2番目)。16個の領域を、曲線に沿ってつないだ順に16進数でコード化することで、この正方形領域に1桁の16進数による空間インデックスが付与されます(図の中央)。
空間インデックスの解像度を上げるには、上述の16領域分割と16進数コード化を再帰的に繰り返しつつ16進数コードの桁を上げていけばよいのです。すなわち、$N$桁の16進数による空間インデックスは、元の正方形領域を$16^N$個の領域に分割したときの解像度を保持しています(図の右側)。
16分割領域と位置情報との紐付け
前章で説明したように、16個の点を結んで得られるインベーダゲームのインベーダのような形が、ヒルベルト曲線による16進数インデックスの基本パターンとなります。
16進数の桁を上げる毎に、各領域に基本パターンを適切な方向に向けて嵌め込んでいきます。下図の左端の場合を上向きと定義すると、それを時計回りに90度ずつ回転しながら、右向き、下向き、左向き、のパターンが得られます。このパターンの向きを変える演算を、$u$, $r$, $l$, $d$ の記号で表すことにします。それぞれ、up, right, left, downの頭文字から採りました。
16進数と正方領域の16個のセルとの対応付けは、基本パターンを上向きに配置したとき、左下セルから曲線をたどって右下セルに至る順序にしたがって付与します(下図の左端)。16進数の桁をあげる場合、16個のセルのそれぞれに基本パターンを決められた向きで嵌め込みます(下図の右端)。この操作を繰り返し行うことで任意の桁数の16進数コードが得られます。
空間インデックスの生成ルール
この章では、前章で説明したヒルベルト曲線による16進数コード化の手順を、変換ルールとして書き下します。
ルール1:コード変換表
最初に、正方形領域を16分割して得られる各セルを表す16進数コードに、セル重心の$X$座標、$Y$座標、およびセルに嵌め込む基本パターンの方向を対応づけるルールが必要です。このルールを対応表にしたのが下表です。例えば、16進数コードの"A"に対応するセル重心は、右上隅の$(3,3)$であり、そこに嵌め込む基本パターンは上向き$(u)$であることが下表から読み取れます。

ルール2:パターン方向への座標変換
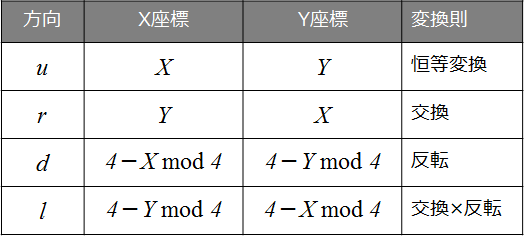
次に必要となる操作は、各セルにおける$(X,Y)$座標を基本パターンの向きに一致するように変換する操作です。$u$, $r$, $d$, $l$ の4方向には、それぞれ、恒等変換、交換、反転、交換×反転の各操作が対応します(下図を参照)。
基本パターンの向きを表す記号$u$, $r$, $d$, $l$ をそのまま対応する座標変換を表す演算子記号として用いることにします(下表)。実際の演算操作では、16進数コードの桁数だけ、座標変換とスケール変換を繰り返すことになります。例えば16進数コードが2桁のコードが"4B"の場合、最初のセル"4"は座標は$(0,2)$で、基本パターンは右向き$(r)$なので、2桁目のセル"B"の座標$(3,2)$の$X$座標と$Y$座標を交換して、スケールを$1/4$に縮小したうえで、1桁目のセル重心に加算します。このコードに3桁目を追加する場合は、2桁目の"B"において基本パターンの向きが左向き$(l)$なので、3桁目のセル座標に"4B"に対応する変換 $lr$、すなわち、(交換×反転)×交換≡反転を行ってから、スケールを$(1/4)^2 = 1/16$に縮小して加算することになります。
桁数だけ座標変換を積算することになるので$u$, $r$, $d$, $l$ の演算ルールをまとめておくと便利です。16進数コードの桁の並び順にしたがって、左から演算子を作用させるとして、以下の等式が成り立ちます。
- $l \equiv r d = d r$($r$ と $d$ は可換)
- $u r = r u = r$
- $u d = d u = d$($u$ は単位元)
- $r r = d d = u$($r, d$ は2回作用して元に戻る)
ルール3:任意の桁数の16進数コードから位置座標への変換
最後に、これまでのルールをもとに任意の桁数の16進数コードから空間座標$(X,Y)$への変換式を導出します。16進数コードの$n$桁目を$Z_n$としたとき、対応する空間座標を$\hat{X}(Z_n)$, $\hat{Y}(Z_n)$、基本パターンの向きを$\hat{c}(Z_n)$と表記します。$n$桁目の座標の向きは、直前の桁に対する相対的な方向なので、絶対的な向き付けは、それ以前の$(n-1)$個の変換演算子$\hat{c}(Z_1)$,...,$\hat{c}(Z_{n-1})$の積により決定されます。さらに、$n$桁目の空間座標は、$(1/4)^n$倍に縮小されています。まとめると、以下の変換公式が得られます。
16進数コード: $Z_1 Z_2 … Z_n … Z_N$
変換後の位置座標: $(X, Y)$
(X, Y) = \sum_{n=1}^N \left({1 \over 4}\right)^n
\left(\prod_{s=1}^n \hat{c}(Z_s) \right)
\left(\hat{X}(Z_n), \hat{Y}(Z_n)\right)
変換事例
前章の変換公式を使って4桁の16進数コードの変換事例を示します。
16進数コード:C4AB

\begin{eqnarray}
(X, Y) &=& \left({1\over4}\right)(3, 1)+ \left({1\over4}\right)^2 d(0, 2)+\left({1\over4}\right)^3 rd (3, 3)+\left({1\over4}\right)^4 urd(3, 2)\\
&=& \left({1\over4}\right)(3, 1)+\left({1\over16}\right)(0, 2) +\left({1\over64}\right)(1, 1)+\left({1\over256}\right)(2, 1)\\
&=& \left({3\over4} + {0\over16} + {1\over64} + {2\over256},
\,{1\over4} + {2\over16} + {1\over64} + {1\over256} \right)\\
&=& \left({198\over256}, \,{101\over256}\right)
=(0.773438, \,0.394531)
\end{eqnarray}
ここで、$180X$を東経、$90Y$を北緯として定義すると、上の結果は、北緯35.507813度、東経139.21875度を表します。Geocoding2で調べると丹沢山の麓にある御殿森という場所であることが分かります。ただし、4桁の解像度は80kmと粗いので東京都港区白金台も御殿森も同じセルに含まれてしまいます。
16進数コードが12桁の場合の解像度を計算すると、正方領域が北緯0~90度、東経0~180度の領域として、1辺の長さが (地球の半径 6400km)×(円周率 3.14) の正方形領域を$(1/4)^{12}$倍に縮小した長さになります。実際に計算すると、以下の通り約1mとなります。
\begin{eqnarray}
&& 6400 \,{\rm km} \times 3.14 \times \left({1\over4}\right)^{12} \fallingdotseq 1\,{\rm m}
\end{eqnarray}
実用上は、12桁以上の桁数が必要そうです。
まとめ
今回は、ヒルベルト曲線を使って位置情報を16進数コードで表す方法について解説しました。本文では16進数コードを緯度、経度に変換する公式を導きましたが、その逆変換として緯度、経度の情報を16進数コードに変換するほうが空間検索の実用上は重要です。実際、ヒルベルト曲線をベースとした高速な空間検索のアルゴリズムが提唱されています4。また、ヒルベルト曲線とは別のZ曲線を使った空間インデックス5や、空間充填曲線の画像処理への応用6についても研究されているようです。



