PythonでBode線図と系の時間応答を求める

制御工学の問題で以下のように出題されたため，sympyによって数値計算させたので備忘録として記録します．（課題内容と数値を変更しています）

問1)
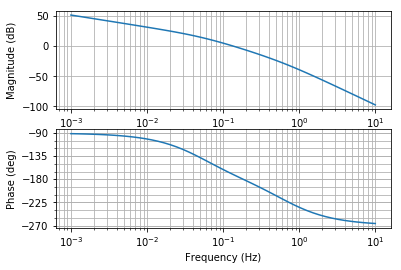
以下の伝達関数のBode線図をかけ．
$$G(s) = \frac{10}{s(s+4)(3s+1)} $$

from sympy import *​

def main():​
    x = Symbol("x")         # symbolとして使う変数の宣言
    y = Symbol("y")
    f = x* (x+4) *(3*x+1)         # 関数f(x)の定義
    f1 = expand(f)          # 関数f(x)を展開
    f2 = factor(f1)         # 関数f(x)を因数分解
    print("f = "+str(f))    # 計算結果の表示
    print("f1 = "+str(f1))
    print("f2 = "+str(f2))
​
if __name__ == '__main__':
    main()

f = x*(x + 4)(3*x + 1)
f1 = 3*x3 + 13*x2 + 4*x
f2 = x(x + 4)*(3*x + 1)
が出力されます．（ただの展開なので頭で計算しても問題ありません．）これより以下のパラメータに係数を入れていきます．

from control.matlab import *
from matplotlib import pyplot as plt

# 伝達関数のパラメータ
num = [ 10]     # 分子の係数
den = [3, 13, 4,0]     # 分母の係数
sys = tf(num, den)  # 伝達関数モデルの作成
bode(sys)           # ボード線図のプロット
plt.show()

ボード線図が出力されました．

問2)
以下の系を制御する場合のシステムの時間応答を求めよ．

\frac{dx(t)}{dt} = \begin{pmatrix} 
0 & 1 \\
-4 & -5\\
\end{pmatrix}x(t) + \begin{pmatrix} 0 \\ 1 \\ 
\end{pmatrix}u(t) \\
x(0) = \begin{pmatrix} 1 \\ 0 \\ \end{pmatrix}, u(t) = Heaviside(t)

from control.matlab import *
from matplotlib import pyplot as plt
import sympy as sym
import numpy as np

def main():
    var("a:z")
    var("A:Z")
 var("X0")
    A = [[0,1], [-4,-5]]
    B = [[0], [1]]
    X0 = [[1],[0]]
    A = sym.Matrix(A)  
    X = (sym.eye(2)*s - A).inv()    
    Y = inverse_laplace_transform(X,s,t) #exp(At)  
    X0 = sym.Matrix(X0)#これはx0
   #print(Y *X0 )#第一項

    #積分の項を計算していく    
    var("tau")#積分のためのtau
    Z = inverse_laplace_transform(X,s,t-tau)#再度計算
    B = sym.Matrix(B)#b
    W = integrate(Z * B ,(tau,0,t))#積分　eAt * b * u(t)
    #print(W)
    Answer = Y * X0 + W

    print(sym.simplify(Answer[0,0]))
    print(sym.simplify(Answer[1,0]))

if __name__ == "__main__":
    main()

Heaviside(t)/4 + exp(-t)*Heaviside(t) - exp(-4*t)*Heaviside(t)/4
-exp(-t)*Heaviside(t) + exp(-4*t)*Heaviside(t)
と出力されました．これより，$$ x(t)= [x_1(t),x_2(t)]$$とした場合，
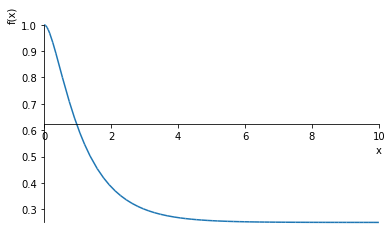
$$x_1(t) = \frac{1}{4} + exp(-t) - \frac{exp(-4t)}{4}$$

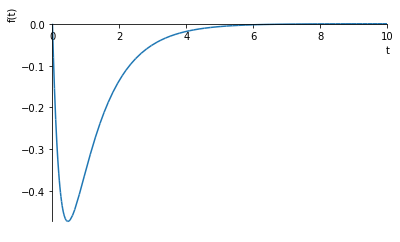
$$x_2(t) = -exp(-t) + exp(-4t)$$
これが解答となりますが，この関数を念のためプロットします．

import sympy as sym
var("t")
sym.plotting.plot((1/4 + exp(-t) - exp(-4*t)/4,(t,0,10)))
sym.plotting.plot(-exp(-t) + exp(-4*t),(t,0,10))

参考になった記事
https://algorithm.joho.info/seigyoriron/python-control-simulation/
https://qiita.com/nnn_anoken/items/ada16e29ef8282498bb7
＋sympyでの数値計算に関する諸々の記事