[入門]二分探索木を解説しながら自力実装してみた
目的
- 二分探索木を学ぶことで、データ構造とアルゴリズムに対する理解を深めたい。
- pythonで二分探索木とデータ構造を実装する。
- データ構造を一次元のリストに畳み込んでしまえば実装は楽かもしれないが、木データ構造の理解を深めるために敢えてノードクラスを定義して二分探索木を実装する
内容
二分探索木の定義
二分探索木とは、順序関係が定義されているノードの値(数値とか順列の定義された文字など)を有した二分木データ構造である。
木構造に関してはこちらを参照。
各ノードは0,1,2個の子ノードを有し、自らより値が小さいものを左子ノード、大きいものを右子ノードと定義されている。
同値のノードに関しては筆者が調べた限り厳密な定義が確認できなかったため、本記事では右子ノードに含める。
場合によっては重複は削除する手法もあるので、注意されたい。
二分探索木の性質
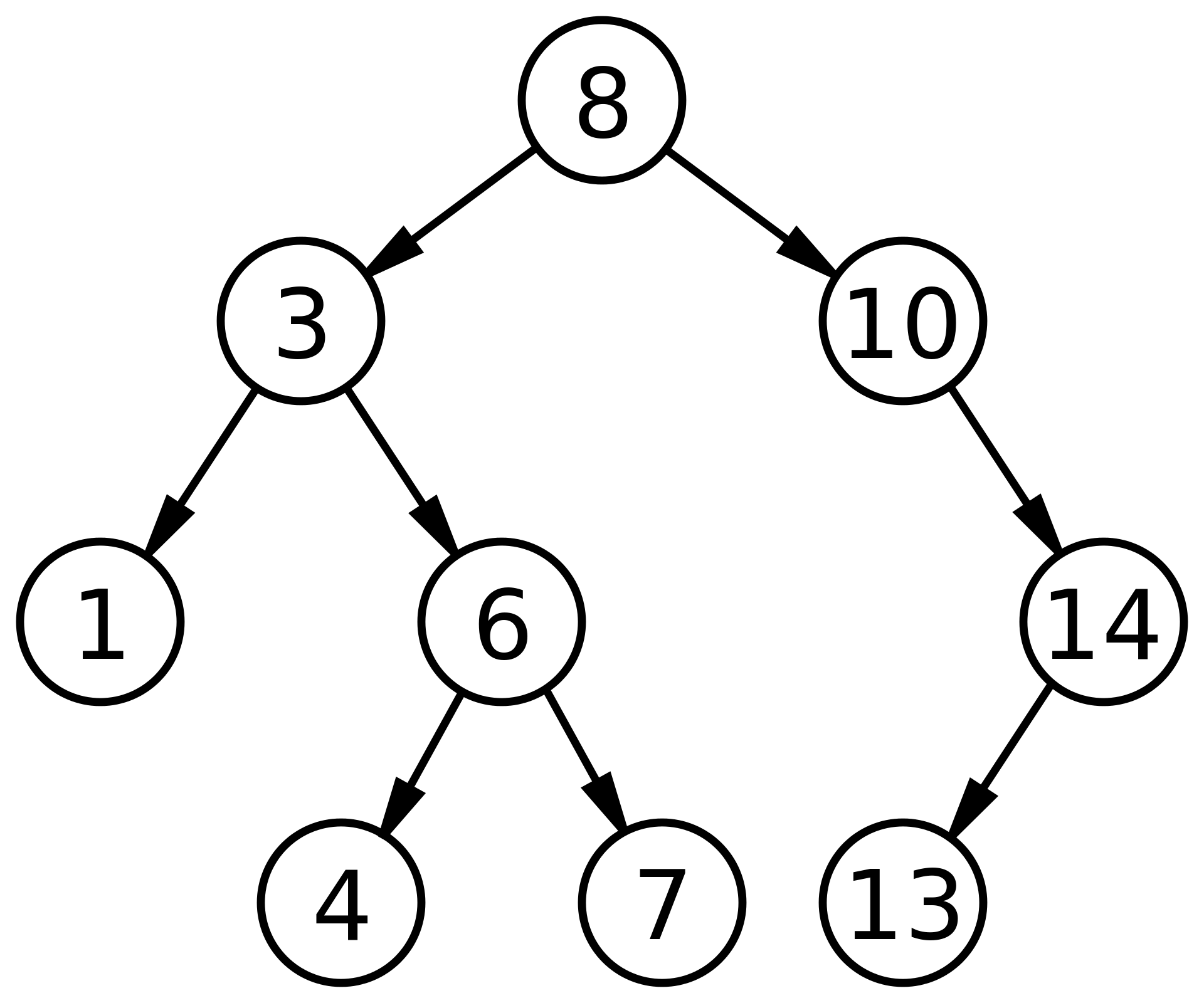
上述の定義のため頂点ノードより小さな値が左分木に、大きい値が右分木に格納されている。この構造は二分探索木のどの位置を切り取っても維持されている。
また、木の左端が集合の最小値、右端が最大値となる性質を有している。
さらに行きがけ順横断(inoder traversal)でノードの値を出力すると、集合が昇順ソートされて出力される。
※誤解なきように注釈するが、この図の13は右端ではない。右端は14である。
13は14ノードの左子であるため右子ノードではない。
実装
二分探索木のデータ構造実装のため、Nodeクラスを定義した。
Nodeクラスはノードの値としての、self.dataと左子self.left右子self.rightの値を有する。
デフォルトの左子と右子はNoneである。
二分探索木の実装のため、BSTクラスを定義した。
コンストラクタで、self.rootを定義しデフォルトをNoneとした。
また新規にノードを追加するためにself.insert(val)を実行している。
メソッドの紹介は以下に示す。
メソッドとして以下を実装した
詳細はコードを参照されたい。
- ノードを追加する
- とある値のノード有無を検査する
- 最小値を得る
- 最大値を得る
- inoderで値を出力する
以下の点がこのデータ構造の面白さだと感じた。
- 二分探索木ではルートからスタートして、値に応じてに左右振り分けするのがポイント。
- 行った先にノートが格納されていれば、そこを起点に更に深く進んでいく。
- 末端にたどり着けばそこで追加する。
- 上から順に振り分けるのが味噌。
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
class BST:
def __init__(self, arr):
self.root = None
for val in arr:
self.insert(val)
def insert(self, val):
if self.root is None:
self.root = Node(val)
else:
node = self.root
flag = True
while flag:
if node.data > val:
if node.left is None:
node.left = Node(val)
flag = False
# whileを終了させるためにFalseをセットする
else:
node = node.left
else:
if node.right is None:
node.right = Node(val)
flag = False
else:
node = node.right
def find(self, node, val):
if node is not None:
if node.data == val:
return True
else:
flag_left = self.find(node.left, val)
flag_right = self.find(node.right, val)
if flag_left or flag_right:
return True
return False
def bst_min(self, node):
if node.left is None:
return node.data
else:
return self.bst_min(node.left)
#再帰で行きついた先の値を返したいときはreturn のあとに再帰関数を書く。traversalのときと用法が異なるので注意。
def bst_max(self, node):
if node.right is None:
return node.data
else:
return self.bst_max(node.right)
def inoder_traverse(self, node):
if node is not None:
self.inoder_traverse(node.left)
print(node.data)
self.inoder_traverse(node.right)
実行
以下のように実行した
import random
arr = [random.randint(1, 100) for _ in range(12)]
ins = BST(arr)
print('insert node list =>', arr)
print('Is there No.4 ->', ins.find(ins.root, 4))
print('root', ins.root.data)
print('min', ins.bst_min(ins.root))
print('max', ins.bst_max(ins.root))
print('--------------------------')
print('通りがけ順で出力するとsortされる')
ins.inoder_traverse(ins.root)
結果
挿入されるリストは毎回変わるので何度か試すと、より理解が深まると思います。
insert node list => [48, 10, 21, 58, 61, 12, 5, 87, 35, 2, 7, 39]
Is there No.4 -> False
root 48
min 2
max 87
--------------------------
通りがけ順で出力するとsortされる
2
5
7
10
12
21
35
39
48
58
61
87