N分木を理解するために解説しながら自力実装してみた
N分木とは
木構造のデータ構造のうち、親ノードの有する子ノードの数がN個以下であるデータ構造の事を指す。
二分木の一般形であるが、第一子ノード(first child)と兄弟ノード(sibling)に分ける事で、結局二分木で表現できる。
二分木で表現できれば、操作や探索は二分木の方法が適用できる。
目的
- N分木を学ぶことで、データ構造とアルゴリズムに対する理解を深めたい。
- pythonでN分木データ構造を実装する。
- 先に二分木を学んだので、その応用としてN分木を学び理解を深める。
- 二分探索木の理解を深めたい。 ⇒ 親記事
内容
データ構造とノードの定義
仮に以下のような複数の子を持つノードを有した木構造を定義する。
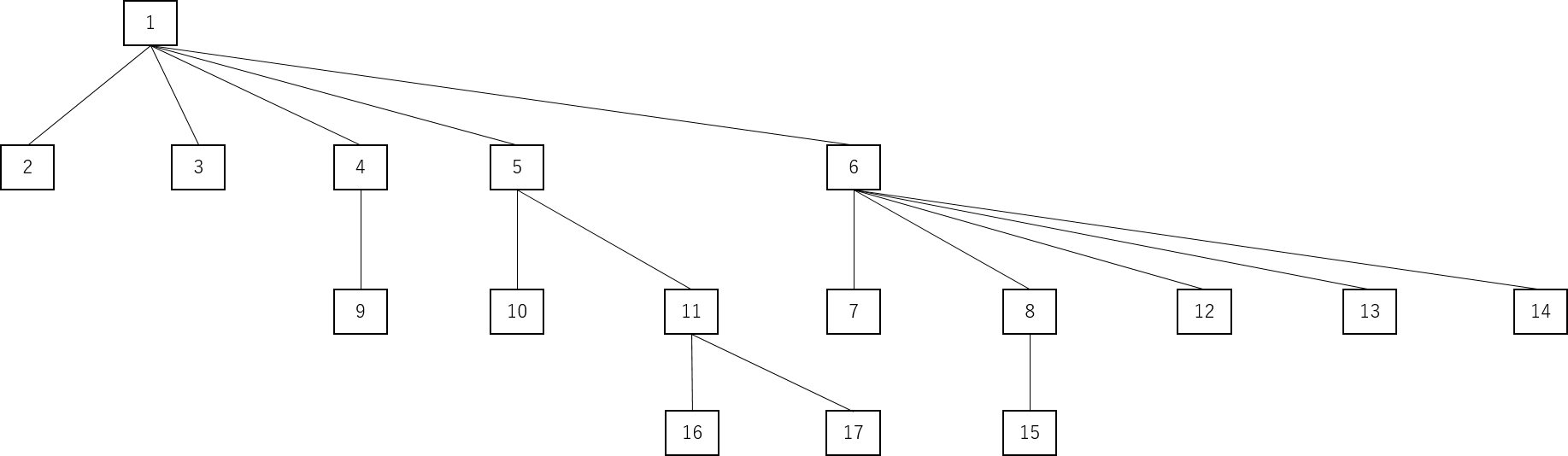
これを実直に実装するならば、ノードクラスを以下の要に定義しなければならない。
class normal_Node():
def __init__(self, data):
self.data = data
self.fist = None
self.second = None
self.third = None
..........
ところで、この様な冗長なノードを定義しても、すべてのノードでこれらの属性を使用するわけではないのでメモリのムダが生じる。
また、子の数が事前に確定していなければ、そもそもノードクラスを定義することが困難になる。
しかしながら、以下の工夫を行うことで、N分木を二分木に再定義出来る。
よって、各ノードは無駄な属性を所持することなく、子の数が不確定でも対応可能となる。
以下に工夫の内容を示す。
- 各ノードは第一子ノードと次兄弟ノードへのリンクを所持する(属性として定義する)
- 各ノードは左から右へ兄弟ノードのリンクを有する
- 最初の子ノードにリンクをする
- 第一子ノード以外は親からのリンクを削除する
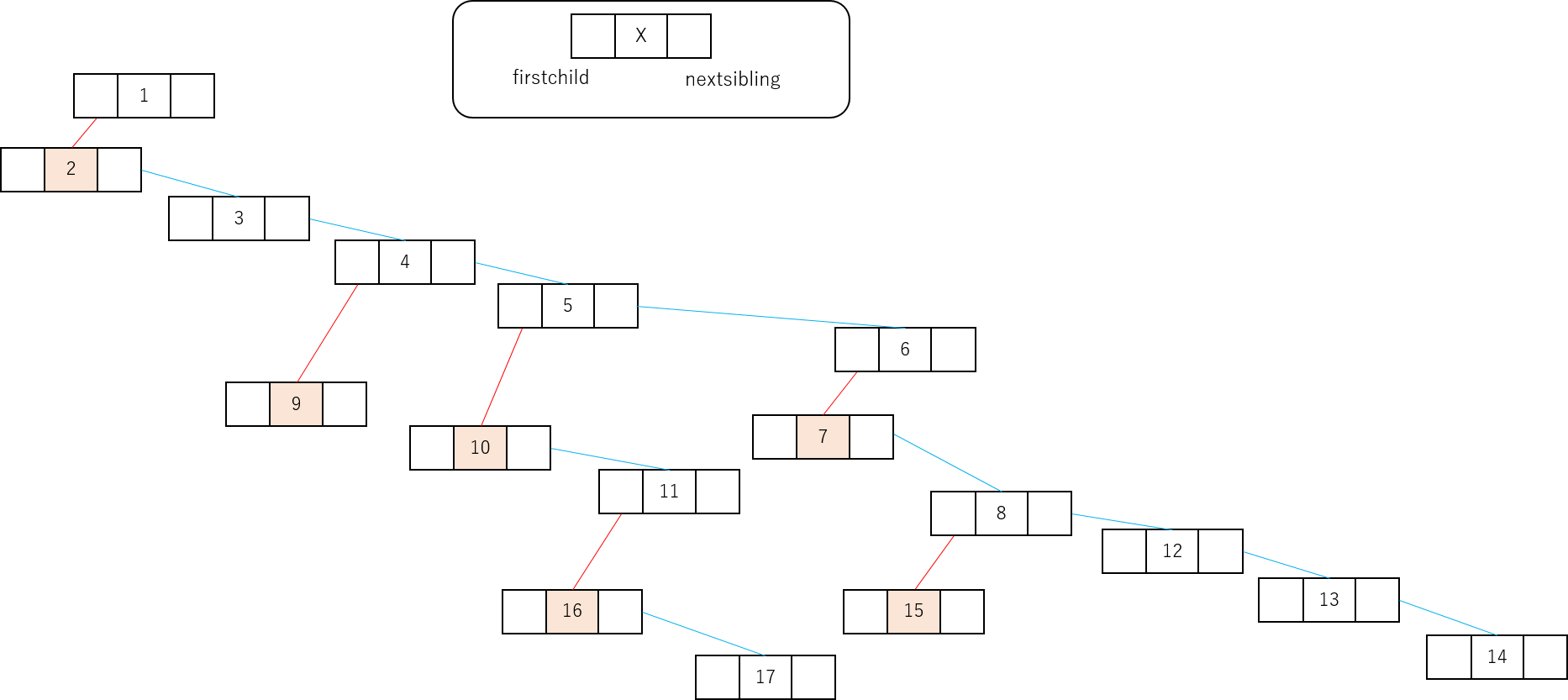
工夫を用いて再構築した木構造は以下の模式図で表せる
赤線はfistchildへのリンク、青線はnextsiblingへのリンクである。
赤ハッチは長子nodeを表す。
二分木実装
Node()オブジェクトの生成
上記内容を実装するためのノードクラスを以下に定義する
class Node():
def __init__(self, data):
self.data = data
self.firstchild = None
self.nextsibling = None
一般木を生成する。
リンクの関係は[親, 子]のリストで与えられる。
同じ親から発生しているリンクは一つのリストにまとめる事とした。
例)
list = [家族1, 家族2, 家族3]
家族1 = [[1, 2], [1,3], [1,4], [1,5], [1,6]]
以下の実装では追加されていくノードの位置をプリント文で出力している。
また、生成した木構造を確認するために間順序横断でノードの値を出力する。
ここでは、子ノード(nextsibling)が先順である。
当然その他の二分木のメソッドも採用できるが、本記事では割愛した。
class Generic_tree:
def __init__(self, node_arr):
self.root = None
for i, family in enumerate(node_arr):
print('try to insert', family, 'in step ', i)
self.insert(i, family)
def insert(self, i, family):
if self.root is None:
print('make root node')
self.root = Generic_tree_Node(family[0][0])
print('make first child for root')
self.root.firstchild = Generic_tree_Node(family[0][1])
temp_node = self.root.firstchild
siblings = [contents[1] for contents in family[1:]] #family のfirstchildはsiblingから除く
print('insert siblings to root.firstchild')
for sibling in siblings:
temp_node.nextsibling = Generic_tree_Node(sibling)
temp_node = temp_node.nextsibling
print('------------------------------')
else:
if i >=1:
pairent = family[0][0]
child = family[0][1]
flag = True
next_queue = [self.root] #初回のqueueを作成
while flag:
temp_queue, next_queue = next_queue, []
for node in temp_queue:
if node.nextsibling is not None:
# print('insert siblings to ', node.data, 'for making queue')
next_queue.append(node.nextsibling)
if node.firstchild is not None:
# print('insert firstchild to ', node.data, 'for making queue')
next_queue.append(node.firstchild)
if node.data == pairent:
print('when you find pairent, insert ', node.data, ' to firstchild')
node.firstchild = Generic_tree_Node(child)
temp_node = node.firstchild
print('insert siblings to ', node.data)
siblings = [contents[1] for contents in family[1:]] #family のfirstchildはsiblingから除く
for sibling in siblings:
temp_node.nextsibling = Generic_tree_Node(sibling)
temp_node = temp_node.nextsibling
print('------------------------------')
if len(next_queue) == 0:
flag = None
def inorder_traverse(self, node):
# 走査の終了条件
if node is None:
return
self.inorder_traverse(node.nextsibling)
print(node.data)
self.inorder_traverse(node.firstchild)
実行は以下のように行った。
node_arr =[
[[1, 2], [1, 3], [1, 4], [1, 5],[1, 6]],
[[4, 9]],
[[5, 10], [5, 11]],
[[6, 7], [6, 8], [6, 12], [6, 13], [6, 14]],
[[8, 15]],
[[11, 16], [11, 17]]
]
ins_generic = Generic_tree(node_arr)
print(ins_generic.root.data)
ins_generic.inorder_traverse(ins_generic.root.firstchild)
結果
try to insert [[1, 2], [1, 3], [1, 4], [1, 5], [1, 6]] in step 0
make root node
make first child for root
insert siblings to root.firstchild
------------------------------
try to insert [[4, 9]] in step 1
when you find pairent, insert 4 to firstchild
insert siblings to 4
------------------------------
try to insert [[5, 10], [5, 11]] in step 2
when you find pairent, insert 5 to firstchild
insert siblings to 5
------------------------------
try to insert [[1, 2], [1, 3], [1, 4], [1, 5], [1, 6]] in step 0
make root node
make first child which is 2 for root
insert siblings to root.firstchild
------------------------------
try to insert [[4, 9]] in step 1
when you find 4 which is pairent, insert 9 as firstchild.
insert siblings to 4 .
------------------------------
try to insert [[5, 10], [5, 11]] in step 2
when you find 5 which is pairent, insert 10 as firstchild.
insert siblings to 5 .
------------------------------
try to insert [[6, 7], [6, 8], [6, 12], [6, 13], [6, 14]] in step 3
when you find 6 which is pairent, insert 7 as firstchild.
insert siblings to 6 .
------------------------------
try to insert [[8, 15]] in step 4
when you find 8 which is pairent, insert 15 as firstchild.
insert siblings to 8 .
------------------------------
try to insert [[11, 16], [11, 17]] in step 5
when you find 11 which is pairent, insert 16 as firstchild.
insert siblings to 11 .
------------------------------
1
6
14
13
12
8
15
7
5
11
17
16
10
4
9
3
2
以上。