きっかけ
量子計算はアナログコンピュータみたいだ、と言われているのをよく眼にします。
確かにそんな気もするのですが、はたしてそれを判断できるほど自分はアナログコンピュータについて知っているのだろうかと自問してみるとなにも知らないことに気が付きました。
そこで analog computer とかで検索してみると、オペアンプを使ったアナログコンピュータ以外にも
水を使った計算機とか出てきてなかなか愉快です。
いろいろ見ているうちに、ダイヤルが3つ付いているだけの箱の写真が出てきました。
Edmund Scientific という会社が教育用アナログコンピュータとして売っていたものだそうです。
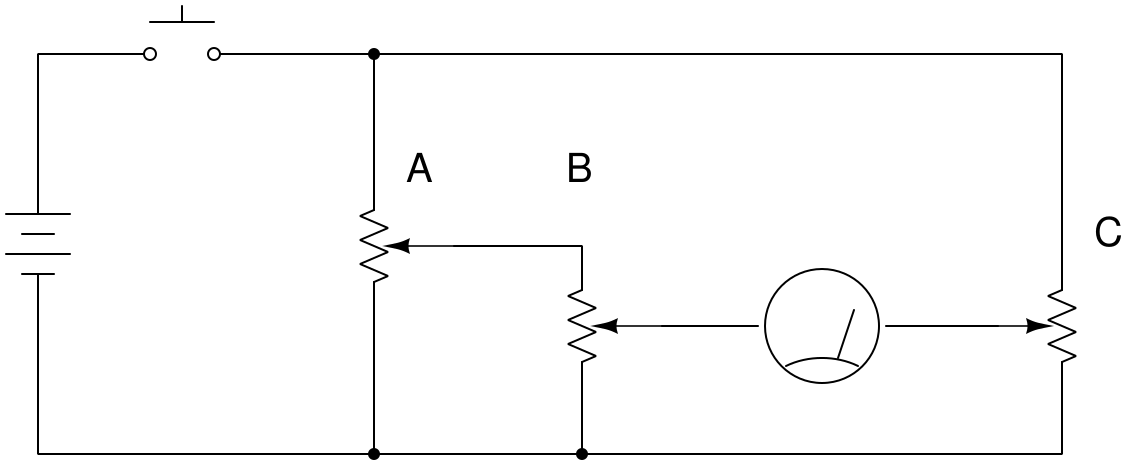
回路図もあって、見ると可変抵抗器3つと検流計があるだけのシンプルな回路で、これで掛け算ができるなどと書いてあります。
動作原理
本当にこれで掛け算ができるのか考えてみます。
3つのダイヤル A, B, C があるのですが、
ダイヤル C のスライド部分は検流計でダイヤル B のスライド部分に繋がっていて、
検流計の針が0のときに両者の電圧は同じになります。
ダイヤル A, B, C のどれか2つ入力値に設定し、
残った一つのダイヤルを動かして検流計の針が0になるところを探る、
という操作ができそうです。
ダイヤル A, B の部分について考えることにします。
ダイヤル A の可変抵抗全体の抵抗値を $A$ とします。
可変抵抗の一方(図の下端の接点)からスライド部分までの抵抗を $a$ とすると
反対の端までの抵抗は $A - a$ です($ 0 \le a \le A $)。
同様に、ダイヤル B の可変抵抗全体の抵抗値を $B$ とします。
可変抵抗の一方(図の下端の接点)からスライド部分までの抵抗を $b$ とすると
反対の端までの抵抗は $B - b$ です($ 0 \le b \le B $)。
ダイヤル A, B は図のように接続されているので、A のスライド部分の電圧は電源電圧 $E$ を
\begin{align}
& A - a : \frac{1}{\frac{1}{a} + \frac{1}{B}} \\
= & A - a : \frac{a \times B}{B + a} \\
= & (A - a) \times (B + a) : a \times B
\end{align}
に分圧することから
\begin{align}
& (A のスライド部分の電圧) \\
= & E \times \frac{a \times B}{(A - a) \times (B + a) + a \times B} \\
= & E \times \frac{a \times B}{A \times B + A \times a - a^2}
\end{align}
のように計算できます。B のスライド部分は更にこれを
$B - b : b$
に分圧したものとなりますから、
\begin{align}
& (ダイヤル B のスライド部分の電圧) \\
= & E \times \frac{a \times B}{A \times B + A \times a - a^2} \times \frac{b}{B} \\
= & E \times \frac{a \times b}{A \times B + A \times a - a^2}
\end{align}
と計算できます。
抵抗値 $A$ が抵抗値 $B$ に比べて十分小さいなら、$a$ の値も $B$ に比べて十分小さいので
$A \times B + A \times a - a^2$ は $A \times B$ で近似できます。
すると、上記の電圧は
\begin{align}
\fallingdotseq & E \times \frac{a \times b}{A \times B} \\
= & E \times \frac{a}{A} \times \frac{b}{B}
\end{align}
となります。つまり、ダイヤル A の角度とダイヤル B の角度を掛け算した値が電圧として得られます。
ダイヤル C を動かして検流計の針が0となる場所を探すと、ダイヤル C の示す値はダイヤル A とダイヤル B を掛け算した値となるわけです。
誤差
$A \times B + A \times a - a^2$ の $A \times B$ からのズレが誤差ですが、この値はどのくらいなのか考えてみます。
当方が見かけた回路図だと、A が 50Ω、B が 1KΩとなっていました。最も誤差が大きくなるのは a=25Ωのときで
\begin{align}
& 1 - \frac{A \times B + A \times a - a^2}{A \times B} \\
= & 1 - \frac{50 \times 1000 + 50 \times 25 - 25^2}{50 \times 1000} \\
= & -0.0125
\end{align}
1.25% 本来の値より下回ることになります。
ダイヤルや検流計の読み取り精度はそれほど高くないのと、そもそも教育用なので、この程度の誤差はあっても問題にはならないのだと思います。
応用
ダイヤル A と B に値を設定し、検流計の針を見ながらダイヤル C を動かして掛け算の結果を得るということが可能なのはわかりました。
ダイヤル C に被除数を、ダイヤル A に除数を設定して、同様に検流計の針が0になるポイントを探りながらダイヤル B を動かすと除算もできそうです。
さらに各ダイヤルに付ける目盛りを工夫するといろいろな計算ができそうです。例えばダイヤルに対数目盛りが振ってあれば
\begin{align}
e^\frac{a}{A} \times e^\frac{b}{B} = & e^\frac{c}{C} \\
→ \frac{a}{A} + \frac{b}{B} = & \frac{c}{C}
\end{align}
のように足し算ができます。足し算ができれば、除算と同じ要領で引き算もできます。
一般化して書くと、各ダイヤルに関数 $f$, $g$, $h$ の目盛りを付けてやれば
$ f(\frac{a}{A}) \times g(\frac{b}{B}) = h(\frac{c}{C}) $
を満たす $a$, $b$, $c$ の組を計算できるわけです。
まとめ
ポテンショメータ3つと検流計で計算ができる、というのはなかなか面白いと思いました。
とはいえ計算尺と比べると、やっていることは同じなわりに操作が面倒臭そう(うっかりすると検流計に大電流が流れる)、ダイヤルを読み取りやすくするにはそれなりの大きさで作る必要があるので場所もとる、とあまりいいところはありません。
回路は簡単なので作ってみたい気もするのですが、意外にポテンショメータは高いので結構な出費になってしまいそうです。